[机器学习] UFLDL笔记 - Convolutional Neural Network - 反向传播与梯度计算

Posted 2023-02-03 WangBo_NLPR

前言

　　本文是我在学习卷积神经网络（Convolutional Neural Network）时的笔记，内容涉及CNN的反向传播、梯度计算等，主要解释了反向传播中Conv层（卷积层）和池化层（Pooling层）之间误差的传递过程和数学表达形式，本文参考资料是Andrew Ng老师在UFLDL Tutorial中的相关章节。关于CNN的笔记在网络上很多了，本文不再详述各种概念细节，只对其中容易混淆和难以理解的算法理念和算法细节做一个讲解。
文章小节安排如下：
　　1）矩阵运算回顾
　　2）Pooling层误差传递到卷积层
　　3）卷积层误差传递到Pooling层
　　4）Pooling层与卷积层之间的权重偏导数计算：Conv Kernel
　　5）卷积层与Pooling层之间的权重偏导数计算：Pooling Kernel
　　

一、矩阵运算回顾

　　CNN中涉及的矩阵操作无非就是矩阵乘积（matrix product）、元素对应乘积（element-wise product）、卷积操作（convolution）、相关操作和克罗内克积（kronecker product），在讨论CNN的反向传播和梯度计算之前，我们先得搞清楚这几种矩阵操作的计算过程。详细的解释可以参考我之前的文章：[机器学习] UFLDL笔记 - Convolutional Neural Network - 矩阵运算。
　　这里做一个简单回顾：
　　
　　1. 矩阵乘积（matrix product）
　　

　　

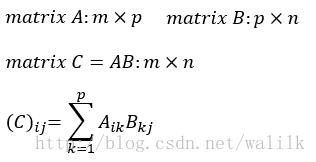
2. 元素对应乘积（element-wise product）/Hadamard乘积

　　
　　

3. 卷积操作（convolution）

　　
　　

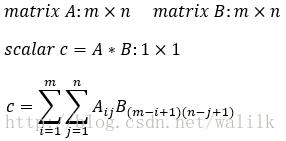
4. 相关操作

　　
　　

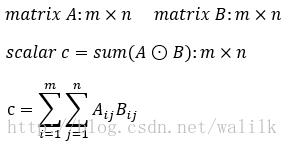
5. 克罗内克积（kronecker product）

　　
　　

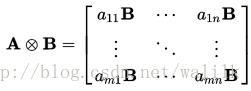
二、Pooling层误差传递到卷积层

　　这里讨论的是在反向传播中，Pooling层的误差是如何传递到Conv层的，或者说，如何根据Pooling层的误差来计算Conv层的误差。
　　

2.1 Upsample

　　上述问题用图来描述的话，我们讨论的就是如下计算过程：
　　

　　即，根据Pooling层(第 l+1 层) 的featuremap的误差计算Conv层(第 l 层) 的featuremap的误差，注意，Conv层和Pooling层的feature map是一一对应的。
　　
　　看一下UFLDL中对Upsample的定义：
　　 The upsample operation has to propagate the error through the pooling layer by calculating the error w.r.t to each unit incoming to the pooling layer.
　　

Upsample的大概思想是：

　　 Pooling层的每个节点是由卷积层中多个节点(一般为一个矩形区域)共同计算得到，所以Pooling层每个节点的误差值也就是由卷积层中多个节点的误差值共同产生，因此需满足Pooling层和Conv层之间的误差值相等。
　　
　　

Upsample的数学表达如下：

　　
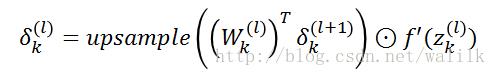
　　这里首先执行一个卷积操作（W与δ的卷积操作，后续会说明），然后执行一个Upsample操作，最后还需要执行一个Hadamard product操作（即Upsample后的featuremap中节点乘以Conv层激励函数的导数值）。式子相对简单，我们可以对比一下普通多层神经网络中的误差计算公式：
　　
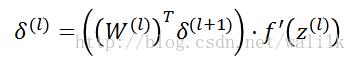
　　两个式子基本是一致的， 可以将普通多层神经网络理解为一个featuremap的size是1x1且每一层都是全连接的CNN，这样普通多层神经网络和卷积神经网络就可以在数学表达形式上统一起来了。
　　
　　关于 这个式子的计算过程，是需要结合具体的Pooling操作形式来决定如何执行Upsample操作。这里更多的是为了阐述一种计算理念，而非具体的计算，所以我们的侧重点应该是去理解Upsample在CNN反向传播中的内在意义，其次才是关注具体的计算过程。 在后续我会将“Pooling层误差传递给Conv层”和“Conv层误差传递给Pooling层”两个过程的计算理念和计算过程统一起来，并尝试说明，CNN中的核心计算就是卷积操作！
　　
　　下面我们就具体讨论两种Pooling操作对应的Upsample操作。
　　

2.2 Mean Pooling模式下的误差传递

　　UFLDL对Mean Pooling的定义如下：
　　if we have mean pooling then upsample simply uniformly distributes the error for a single pooling unit among the units which feed into it in the previous layer.
　　意思是说：如果采用mean-pooling，那么就把pooling层单元的error，均匀分配给卷积层对应的单元。

　　这里用一张图解释Mean Pooling操作下的误差反向传播：
　　

　　注意：average后每个神经节点还需要乘以Conv层激励函数的导数值，这里并没有绘制。
　　
　　 注意，上图并没有正确的反映出Upsample的数学计算公式，只是一种直观的容易的理解方式，同时也可以作为编程实现的方式。正确的Upsample操作计算过程如下：
　　
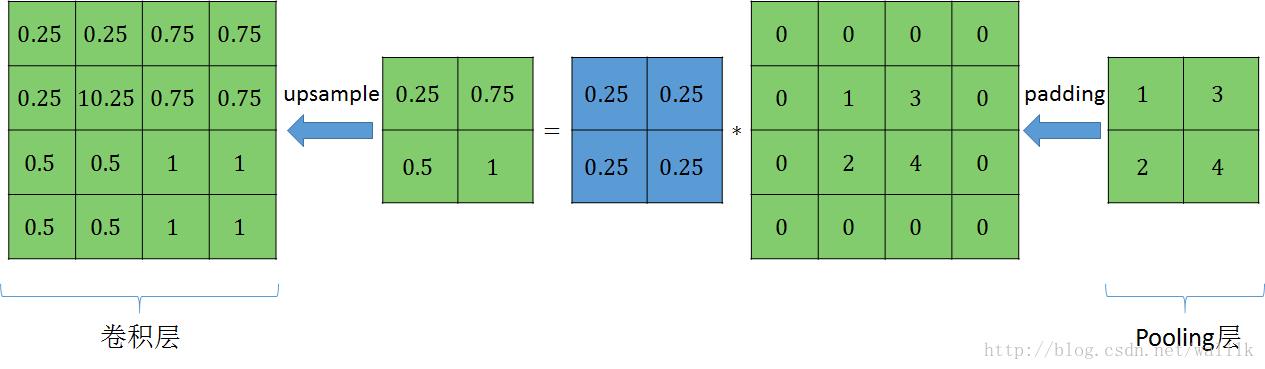
　　这里首先执行的是一个 离散卷积操作，然后对计算结果进行 Mean Pooling模式下的Upsample操作，得到卷积层featuremap对应的error map。由此我们也可以看到， Pooling层误差传递到卷积层的计算过程，核心是卷积操作！
　　

2.3 Max Pooling模式下的误差传递

　　UFLDL对Mean Pooling的定义如下：
　　In max pooling the unit which was chosen as the max receives all the error since very small changes in input would perturb the result only through that unit..
　　意思是说：如果采用max-pooling，那么“卷积层feature map中指定区域（看下面的图示）”的最大激活值单元将接收所有的误差，为啥它接收所有误差呢？因为输入的任何微小变化，都会通过这个最大激活值单元向前传递，所以误差也自然是由该单元来接收。因此，如果采用max-pooling的话，则需要记录前向传播过程中pooling区域中最大值的位置（在feature map中的位置）。
　　
　　这里还是用一张直观的图解释Max Pooling操作：
　　

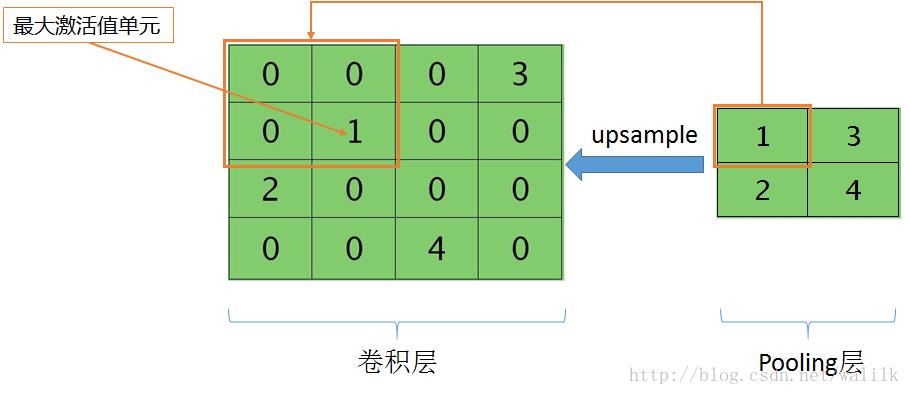
　　upsample后每个神经节点还需要乘以Conv层激励函数的导数值，这里并没有绘制。 需要注意的是，如果在前向传播中采用max-pooling，则需要记录前向传播计算过程中max pooling区域中最大值的位置，以便在反向传播时正确的传递误差。
　　
　　 同样的，上图并没有正确的反映出Max Pooling模式下Upsample的数学计算过程，各位可以自行绘制Max Pooling模式下，误差从Pooling层传递到Conv层的完整计算过程。
　　
　　

三、卷积层误差传递到Pooling层

　　这里讨论的是在反向传播中，Conv层的误差是如何传递到Pooling层的，或者说，如何根据Conv层的误差来计算Pooling层的误差。
　　

3.1 误差传播过程

　　上述问题用图来描述的话，我们讨论的就是如下计算过程：
　　

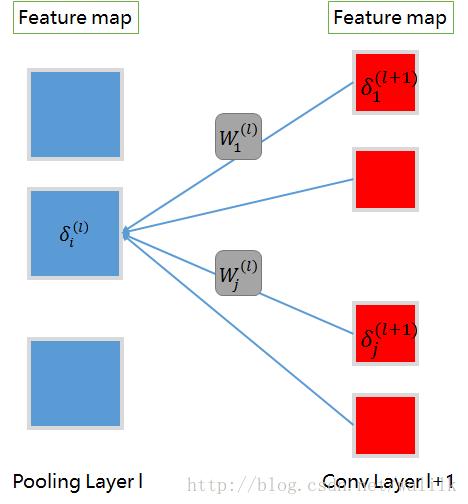
　　 从图中可以看出，Pooling层的一个feature map会对卷积层的所有feature map有影响，因此在反向传播误差时，卷积层的所有feature map都会将误差传递给Pooling层的这个feature map（通过权重矩阵kernel），并累加得到最终的误差矩阵。
　　

3.2 误差传播计算说明

　　第 l 个Pooling层第 i 个feature map的误差矩阵计算公式如下：
　　

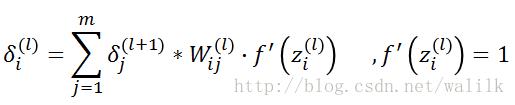
　　参考前面的图示并不难理解这个公式，说明三点：
　　1）* 是卷积操作，在执行卷积操作前，需要先对δ(l+1)进行padding；
　　2）f’(z)=1是因为Pooling层在执行Pooling操作后并没有做非线性激活；
　　3）第 l 个Pooling层中每个特征图的误差值，其计算依据为第 l+1 个Conv层所有feature map的误差贡献之和。
　　
　　在这里执行的是真正意义上的 离散卷积，不同于卷积层前向传播时的相关操作。
　　
　　假定Conv层只有两个featuremap，那么我们可以用图来描述误差传递的计算过程如下：
　　
　　注意理解其中的离散卷积操作，并记住， 前向传播时候，l 层一个节点对 l+1 层 n 个节点有影响，那么在反向传播误差时，l 层就需要从 l+1 层的这 n 个节点接收误差。只要是神经网络及其延伸出来的各种网络结构，这点都是适用的。
　　

四、Pooling层与卷积层之间的权重偏导数计算：Conv Kernel

　　有了激励值（featuremap）和误差值（errormap），那么计算梯度就是非常容易的事情。　　

4.1 Conv Kernel

　　先看一下我们计算的是哪个参数矩阵的梯度：
　　

　　这里要注意理解卷积核 W ^(l) _ij和b ^(l) _j，如图，这里是Pooling Layer l 的第 i 个featuremap与Conv Layer l+1的第 j 个featuremap之间的权重矩阵和偏置项。
　　

4.2 Conv Kernel的梯度计算

　　Pooling层与卷积层之间的权重偏导数计算公式如下：
　　

　　
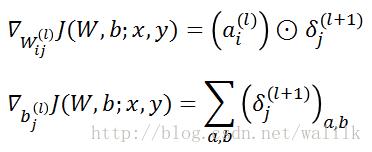
　　为了数学表达上的简洁，这里我们用⊙代表相关操作，我们可以把 误差矩阵δ 看作是卷积核，与 特征图a 进行卷积操作，图示如下：
　　
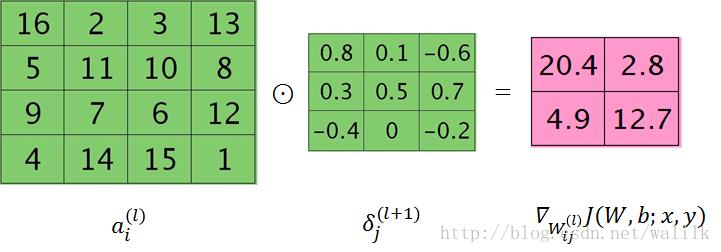
　　我们还是对比一下普通多层神经网络的权重矩阵偏导数计算公式：
　　 　　
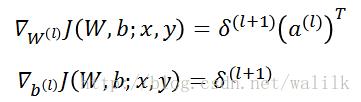
　　两者形式行依然是一致的，这也就说明， CNN不是凭空出现的黑科技，CNN与普通多层神经网络是一脉相承的，因此我们在做CNN方面的研究时，一定要多参考多层神经网络的研究成果。
　　

五、卷积层与Pooling层之间的权重偏导数计算：Pooling Kernel

　　Pooling操作的kernel - 权重矩阵是固定的，例如mean-pooling或者max-pooling，因此不需要进行更新权值，也就不需要求所谓权值的导数了。
　　

六、结语

　　基于卷积层、Pooling层和全连接层的卷积神经网络时CNN的基础网络结构，其他任何复杂的深度网络结构也无外乎本文中所涉及的这些计算模式或类型：偏导数、梯度、卷积、Pooling、激励值的前向传播、误差的反向传播……等等等。因此如果想要深入学习深度学习，打好这些基础非常重要！
　　再次强调，在CNN中，卷积操作是核心！
　　
　　本文的文字、公式和图形都是笔者根据所学所看的资料经过思考后认真整理和撰写编制的，如有朋友转载，希望可以注明出处：
　　[机器学习] UFLDL笔记 - Convolutional Neural Network - 反向传播与梯度计算
　　http://blog.csdn.net/walilk/article/details/78498690