matlab生鲜或农产品（河马等）配送路径优化研究matlab优化算法十八

Posted 2023-01-30 张叔zhangshu

生鲜农产品的定义

生鲜农产品是指可以直接在货架上出售而无需再进行进一步制作的现场加工的鲜果等初级产品。目前，生鲜农产品主要具体包括新鲜上市的蔬菜、水果、花卉、蛋、奶、生禽和水产品以及鲜肉产品，这些种类的产品在生鲜农产品中占据主要地位，习惯将其称为生鲜三品—一果蔬、肉类、水产

研究目的

本文的主要研究目的是在降低物流配送成本、提升配送效率、保持生鲜农产品的新鲜度及及时度的基础上，着重考虑配送车辆基于配送中心、交通路线规划、智能配送模式的基础，规划岀最合理的车辆配送路径以达到供需双方的共同满意的结果。通过对生鲜农产品的特点进行归纳整合，并考虑配送时间等相关约束条件，建立一个更加准确、详尽的定义关于生鲜农产品配送的车辆路径问题的数学模型，并且为其找到比较实用简单的求解方法，以求实现生鲜农产品在配送过程中实现产品保鲜保质达到客户满意度要求的同时实现配送成本最低达到效益最大化

研究方法与思路

本文在前人研究成果的基础上，了解了生鲜农产品配送的相关知识与内容，并对其配送路径进行了分析与进一步的探索，明确车辆路径的优化目标及其规划，具体采用以下研究方法：
（1）文献法：通过査看国内外有关双向物流配送、生鲜农产品运输、时间窗求解、车辆路径规划等相关文献硏究，学习有关生鲜品配送及带时间窗的车辆路径的理论，为论文的创作提供有力的理论依据。
（2）模型法：通过对生鲜农产品配送模式的分析和总结，建立适合生鲜农产品配送目标的车辆路径与模型，为生鲜农产品配送的发展提供理论基础
（3）模拟分析法：通过模拟实验的数据分析，判断是否有效。
通过将研究方法与研究内容结合后，研究思路主要有以下几步：
（1）对生鲜农产品的配送模式及相关理论研究状况进行深入研究；
（2）通过对于生鲜农产品特点及配送模式的分析，了解其基础及相关理论对其车辆路径问题在时间窗理论基础上进行进一步探索。
（3）针对生鲜农产品的特点及车辆路径问题的研究，与现有的研究方法结合，建立带时间窗的车辆路径模型选择，并使用遗传算法对于模型进行求解。

生鲜农产品配送的特点

与普通的产品配送相比，生鲜农产品由于其自身的独特属性，在物流配送方面也有着不同的要求。而随着经济水平与消费水平的提升，生鲜农产品的的配送市场需求量大，配送对象也各有不同，总体概括来说，关于生鲜农产品的物流配送特点有以下几点：
（1）配送成本高。产品在进行配送过程中影响整个物流成本的因素众多，普通产品来说包含人工成本、车辆消耗及维护成本、储存成本等，而生鲜农产品基于其自身的属性特点，除了以上几点常规因素外，配送成本还受到以下几点约束：
①产品自身损耗。生鲜农产品具有易腐、易烂的显著特点，在配送过程中会遭受不可避免地磕碰、闷热、挤压等问题，必然会损害产品的完整度及新鲜度，造成产品自身的损耗。
②储存方式。而正是由于生鲜农产品极易损耗的特征，同样在配送过程中会给储存带来一定的难度，对于技术、方式、储存空间都有极高的要求，相比于普通产品来说必然会额外增加产品的储存成本。
（2）时效性。由于市场对于生鲜农产品的需求量大，具体配送过程中关于生鲜农产品的订单涉及的生鲜农产品种类、数量、特征不一，且可能存在订单需求方不同的多目标配送等状况，此时结合生鲜农产品的特有属性就需要在配送过程中进一步的提升配送速度以保障生鲜农产品的新鲜度及客户对生鲜农产品配送的满意度
（3）品类多。随着经济水平的提升，生鲜农产品的类型也随着科技养殖手段进一步丰富，市场对于生鲜农产品的需求也趋于多样化。特别是对于小型客户如家庭为单位、宾馆、小型餐馆等的订单，往往对于生鲜农产品的选择更加丰富多样，则就要求生鲜农产品在由生产基地送往配送中心再由配送中心送往客户手中的过程要丰富生鲜商品的种类及配送方式，才能让客户有更多的选择，以便提供更优质的服务。

模型约束条件

（1）达到客户对整体配送服务及质量的需求时间段的满意度；
（2）达到客户关于生鲜农产品送达时质量的满意度；
（3）限制每一辆配送车辆的装载量，不允许超过车辆的载重量和容量；
（4）每种类型的生鲜农产品初始新鲜度、损耗情况一致；
（5）达到客户对生鲜农产品类型、质量、数目的满意度，同时实现所有产品同时配送；
（6）每位目标客户只有一种运输工具为其服务；
（7）不考虑车辆行驶中的速度变化、道路拥堵等情况。

顾客满意度

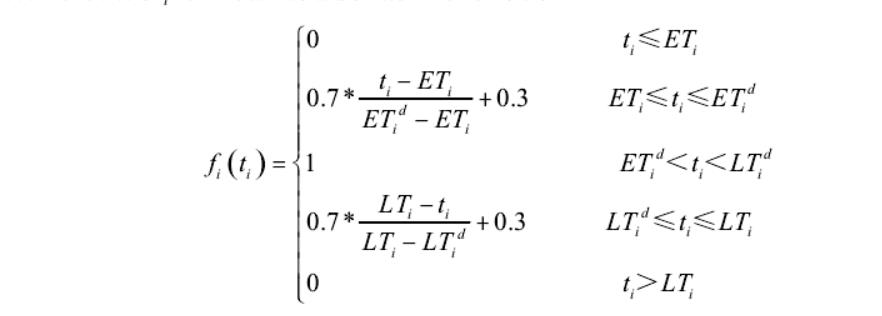
模型

式中：
（5.1）为目标函数，表示配送成本最小。
（5.2）为顾客满意度约束，意思时顾客满意度的平均值要在以上。
（5.3）为车辆装载能力约束
（5.4）用来确保顾客仅由第p组车的第q辆车完成配送。
（5.5）、（5.6）表示到达某一顾客的车辆的唯一约東，即每一顾客有且仅有辆车为其服务。

主程序

clear
clc
close all
tic
%% 用importdata这个函数来读取文件
% shuju=importdata('cc101.txt');
load('c101');
shuju=c101;
% bl=importdata('103.txt');
bl=0;
cap=1500;                                                        %车辆最大装载量
%% 提取数据信息

E=shuju(1,5);                                                    %配送中心时间窗开始时间
L=shuju(1,6);                                                    %配送中心时间窗结束时间
zuobiao=shuju(:,2:3);                                       %所有点的坐标x和y
% vertexs= vertexs./1000;
customer=zuobiao(2:end,:);                                       %顾客坐标
cusnum=size(customer,1);                                         %顾客数
v_num=6;                                                        %车辆最多使用数目
demands=shuju(2:end,4);                                          %需求量
a=shuju(2:end,5);                                                %顾客时间窗开始时间[a[i],b[i]]
b=shuju(2:end,6);                                                %顾客时间窗结束时间[a[i],b[i]]
s=shuju(2:end,7);                                                %客户点的服务时间
h=pdist(zuobiao);
dist=squareform(h);    
dist=dist./1000;%距离矩阵，满足三角关系，暂用距离表示花费c[i][j]=dist[i][j]
%% 遗传算法参数设置
alpha=100000;                                                       %违反的容量约束的惩罚函数系数
belta=900;%违反时间窗约束的惩罚函数系数
belta2=60;
chesu=30;

NIND=100;                                                       %种群大小
MAXGEN=500;                                                     %迭代次数
Pc=0.9;                                                         %交叉概率
Pm=0.05;                                                        %变异概率
GGAP=0.9;                                                       %代沟(Generation gap)
N=cusnum+v_num-1;                                %染色体长度=顾客数目+车辆最多使用数目-1
% N=cusnum;
%% 初始化种群
init_vc=init(cusnum,a,demands,cap);                             %构造初始解
Chrom=InitPopCW(NIND,N,cusnum,init_vc);
%% 输出随机解的路线和总距离
disp('初始种群中的一个随机值:')

[VC,NV,TD,violate_num,violate_cus]=decode(Chrom(1,:),cusnum,cap,demands,a,b,L,s,dist,chesu,bl);
[~,~,bsv]=violateTW(VC,a,b,s,L,dist,chesu,bl);
% disp(['总距离：',num2str(TD)]);
disp(['车辆使用数目：',num2str(NV),'，车辆行驶总距离：',num2str(TD)]);
disp('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~')
%% 优化
gen=1;
figure;
hold on;box on
xlim([0,MAXGEN])
title('优化过程')
xlabel('代数')
ylabel('最优值')
ObjV=calObj(Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta,belta2,chesu,bl);             %计算种群目标函数值
preObjV=min(ObjV);
while gen<=MAXGEN
    %% 计算适应度
    ObjV=calObj(Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta,belta2,chesu,bl);             %计算种群目标函数值
    line([gen-1,gen],[preObjV,min(ObjV)]);pause(0.0001)%画图 最优函数
    preObjV=min(ObjV);
    FitnV=Fitness(ObjV);
    %% 选择
    SelCh=Select(Chrom,FitnV,GGAP);
    %% OX交叉操作
    SelCh=Recombin(SelCh,Pc);
    %% 变异
    SelCh=Mutate(SelCh,Pm);
    %% 重插入子代的新种群
    Chrom=Reins(Chrom,SelCh,ObjV);
    %% 打印当前最优解
    ObjV=calObj(Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta,belta2,chesu,bl);             %计算种群目标函数值
    [minObjV,minInd]=min(ObjV);
    disp(['第',num2str(gen),'代最优解:'])
    [bestVC,bestNV,bestTD,best_vionum,best_viocus]=decode(Chrom(minInd(1),:),cusnum,cap,demands,a,b,L,s,dist,chesu,bl);
    disp(['车辆使用数目：',num2str(bestNV),'，车辆行驶总距离：',num2str(bestTD)]);
    fprintf('\\n')
    %% 更新迭代次数
    gen=gen+1 ;
end
%% 画出最优解的路线图
ObjV=calObj(Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta,belta2,chesu,bl);             %计算种群目标函数值
[minObjV,minInd]=min(ObjV);
%% 输出最优解的路线和总距离
disp('最优解:')
bestChrom=Chrom(minInd(1),:);
[bestVC,bestNV,bestTD,best_vionum,best_viocus]=decode(bestChrom,cusnum,cap,demands,a,b,L,s,dist,chesu,bl);
disp(['车辆使用数目：',num2str(bestNV),'，车辆行驶总距离：',num2str(bestTD)]);
disp('-------------------------------------------------------------')
[cost,q1,q2,q3,q4,q5,q6]=costFuction(bestVC,a,b,s,L,dist,demands,cap,alpha,belta,belta2,chesu,bl);
%% 画出最终路线图
draw_Best(bestVC,zuobiao);

结果

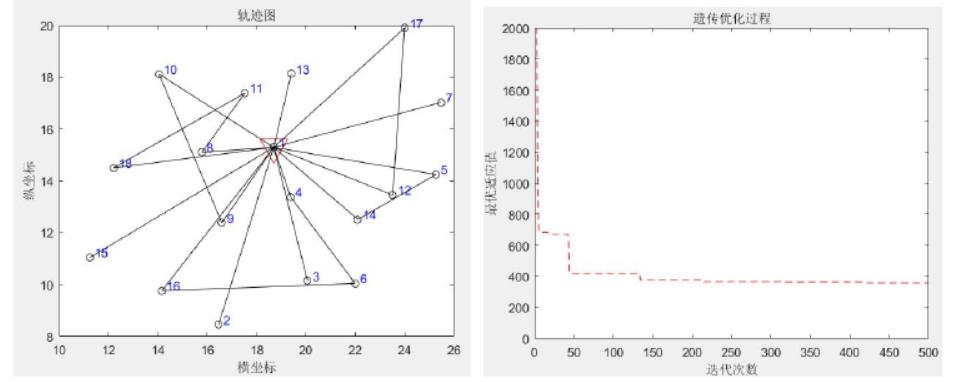
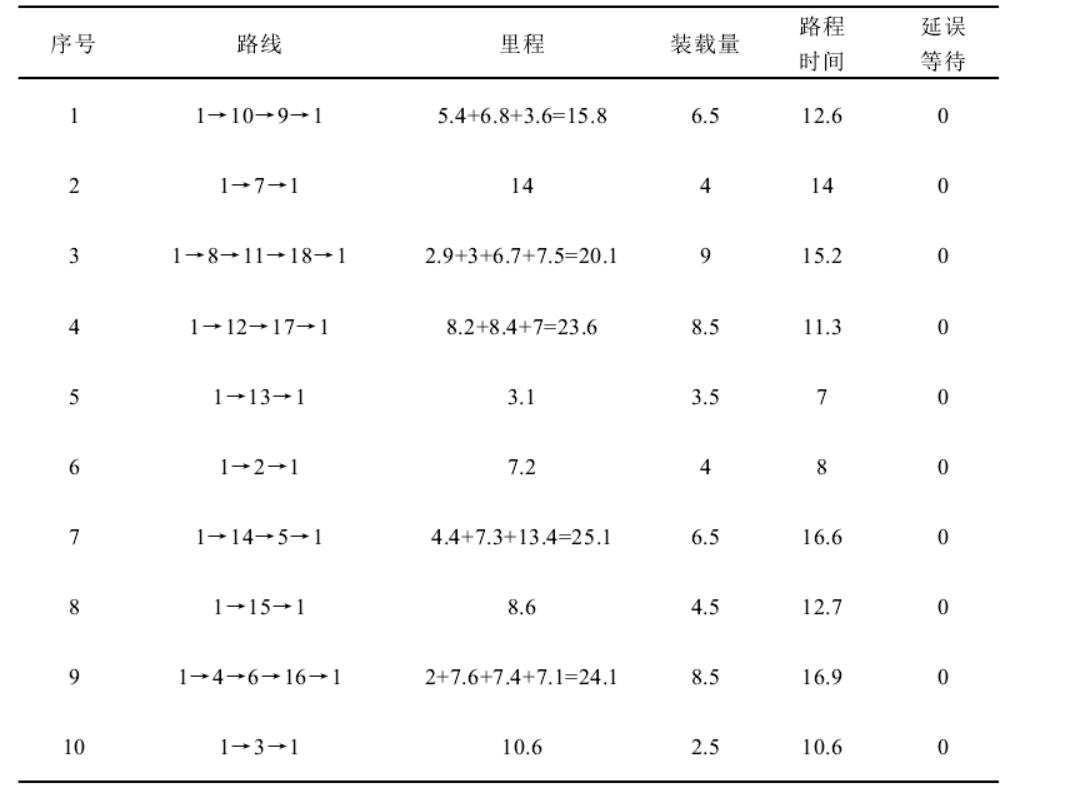
计算结果表明，在9辆车的使用情况下，经过运行得到的最优可行解为1,8，10,1,2,16,1,3,1,18,15,1,7,1,5,1,4,12,14,1,11,13,17，16,9,1，完成整体配送任务后对应的最低配送总成本由10辆车的359.3838元降低到2874416元，行驶总里程为1297735km，同时各车辆运输时间相对平均，没有造成部分车辆用车过度，且各个车辆运输时间不长，基本在12小时左右，能够维持生鲜农产品的新鲜度。通过上述比较可以看出，9辆车的配送结果优于10辆车的配送结果，运输成本和行驶里程都更优，而这意味着在以后的研究过程中，进行配送车辆路径优化的同时可以合理安排车辆的使用进一步的降低整体配送成本，提升配送效率效率。
如需帮忙V：zhangshu2274