从莱斯定理出发看程序分析中的sound与complete

Posted 2023-01-21 3A是个坏同志

莱斯定理是计算理论中非常重要的结论，从它出发也可以明了的分析出针对图灵完备语言进行静态分析的理论上限。莱斯定理的定义是这样的：

Let S be a set of languages that is nontrivial, meaning
there exists a Turing machine that recognizes a language in S
there exists a Turing machine that recognizes a language not in S
Then, it is undecidable to determine whether the language recognized by an arbitrary Turing machine lies in S.

定义首先说明了“非平凡性”这一概念，非平凡性指的是：如果一个属性不对所有的程序都为真或假，即为非平凡。比如程序是否不存在数组越界，是否不存在空指针解引用，都是对于程序的非平凡属性。莱斯定理的内容即为：一个程序是否具备某种非平凡属性这个问题如同停机问题一样，是不可判定的，即不存在一个程序可以判定任意程序具有某种非平凡属性。

既然有这种结论，是不是说明我们没法做程序分析了呢？并不是，因为莱斯定理中的“程序”指的是用图灵机编写的程序。也就是说，如果我们限定到一个非图灵完备语言编写的程序上，莱斯定理就不适用了。比如我们限定程序不能使用循环，这时候一些非平凡属性可能就是可判定的。这个时候我们所判定的程序集合是在一个非图灵完备的DSL框架中。既然存在可判定的DSL，那么对于图灵完备语言所编写的一部分程序也有可能是可判定的——也就是说，对于图灵完备语言，一些情况下我们能做出正确的分析，一些情况下是无法判定的。

因此，我们需要规避一些不可判定的情况，对程序得出一个尽可能“正确”的分析。也就是说，我们的程序分析结果其实都并不是那么“精确”——程序分析允许一定的不精确性。但是它们都是在“安全”或者说“保守”的方向上不精确。在不同的分析应用中，所谓“保守”的方向也各不相同。如通过到达定值分析解决下面这个问题：

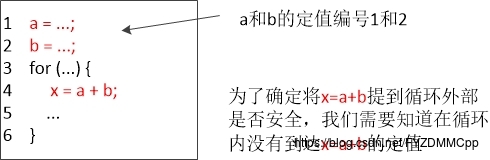
这个问题中，在不知道定值是否会到达某点的情况下假设针对每个赋值变量都产生一个新的定值是保守的。如果得出的解认为不产生新的定值，那么会将x视为循环不变量提出，这个错误的优化改变x的值。在可用表达式分析中，“安全”的定义就和到达定值不同。如果可用表达式没有到达某个程序点，而得出的解表明到达了，则这是不安全的。因为如果一个表达式被认为是可用的，我们有可能会做一些比较危险的事情，例如删除重复计算该表达式的指令。因此在设计一个数据流模式的时候，我们必须知道这些信息将如何被使用，并保证我们做出的任何估算都是在“保守”或者说“安全”的方向上。每个模式和应用都要单独考虑。 

依据这个原则，我们的解要在“保守”的大原则下尽量做到精确。比如数据流分析大多采用迭代分析的框架，那么解就要在迭代的过程中尽力向精确的方向靠近。使用术语来说明这个概念，sound static analysis就对应我们所谓的“保守解”，它是一种“过逼近”，能够覆盖完所有违反所要检验的属性的场景，不过因为它考虑程序中可能实际并不可行的路径，所以会产生误报。complete static analysis则与之相反，是一种“欠逼近”，它产生的解超过精确解，这些值保证都违反了所要检验的属性，但是并不能覆盖完所有的值，有漏报。考虑莱斯定理的概念，complete分析就是一种针对可判定情形的检验，对于其它情形则允许“不知道”，而sound分析则需要进行过度考虑，在许多情形下，静态分析工具并不能做到sound，因为它需要探索过多的执行路径，严重影响接下来分析的精确度，以至于无法得到有效的结果。