强化学习 DQN pytorch实例
Posted 软件工程小施同学
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了强化学习 DQN pytorch实例相关的知识,希望对你有一定的参考价值。
DQN简介
DQN,全称Deep Q Network,是一种融合了神经网络和Q-learning的方法。这种新型结构突破了传统强化学习的瓶颈,下面具体介绍:
神经网络的作用
传统强化学习使用表格形式来存储每一个状态state和状态对应的action的Q值,例如下表表示状态s1对应了两种动作action,每种action对应的Q值为-2和1。
| a1 | a2 | |
| s1 | -2 | 1 |
| s2 | 2 | 3 |
| ... | ... | ... |
但当我们有很多数据时,首先,内存不够是第一个问题;其次,搜索某个状态对应的动作也相当不便,这时就想到了引入神经网络。
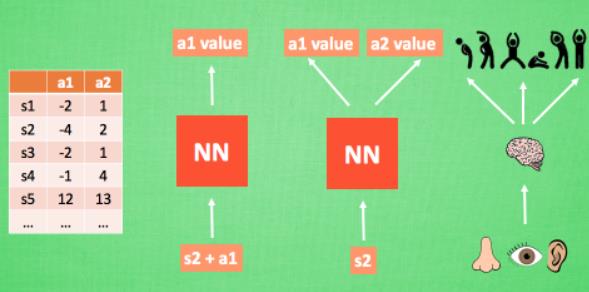
我们可以把状态和动作当作神经网络的输入,然后经过神经元的分析得到每个动作对应的Q值,这样我们就没有必要用表格记录Q值;
或者我们也可以只输入状态,输出所有的动作,然后根据Q-learning的原则,直接选择具有最大Q值的动作作为下一步要做的动作。就好比相当于眼睛鼻子耳朵收集信息, 然后通过大脑加工输出每种动作的值, 最后通过强化学习的方式选择动作。
更新神经网络
神经网络需要被训练才能预测出正确的值。如何更新呢?
假设已存在Q表,当前状态s1有两个对应的action,分别是a1和a2。
根据Q表,选择最大价值的a2,此时进入到状态s2,而 s2也有两个对应的action,分别是a1和a2,选择最大价值的动作,乘以衰减率gamma,加上奖励reward,此时得到的值便是Q(s1,a2)的现实值,
而Q(s1,a2)的估计值直接由Q表给出,此时便有了Q现实与Q估计的差距,然后该差距乘以学习率,再加之前的参数,便得到了最新神经网络的参数。
DQN两大特点
DQN 有一个记忆库用于存储学习之前的经历。Q learning 是一种 off-policy 离线学习法,它能学习当前经历着的, 也能学习过去经历过的, 甚至是学习别人的经历。所以每次 DQN 更新的时候, 我们都可以随机抽取一些之前的经历进行学习。 随机抽取这种做法打乱了经历之间的相关性, 也使得神经网络更新更有效率。
而 Fixed Q-targets 也是一种打乱相关性的机理, 如果使用 fixed Q-targets, 我们就会在 DQN 中使用到两个结构相同但参数不同的神经网络,代码中用target_net、eval_net表示这两种不同的神经网络。
一、前言
实例参考MorvanZhou/Reinforcement-learning-with-tensorflow,
更改为PyTorch实现,并增加了几处优化。实现效果如下。
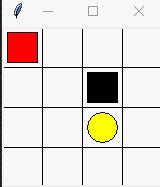
其中,红色方块作为探索的智能体,到达黄色圆形块reward=1,到达黑色方块区域reward=-1.
二、代码
1. maze_main.py
from maze_env import Maze
from maze_RL_brain import DQN
import time
# 注释参考https://www.pancake2021.work/?m=202207
def run_maze():
print("====Game Start====")
step = 0 # 已进行多少步
max_episode = 500 # 总共需要进行多少轮,每轮有多步
for episode in range(max_episode):
# 每一次新的训练
# 开始,会重置我们的env, 每一次训练的环境都是独立的而完全一样的,只有网络记忆是一直留存的
state = env.reset() # 重置智能体位置,# 获得初始化 observation 环境特征
step_every_episode = 0 # 本轮已进行多少步
epsilon = episode / max_episode # parameter for epsilon greedy policy,动态变化随机值
# 开始实验循环
# 只有env认为 这个实验死了,才会结束循环
while True:
if episode < 10:
time.sleep(0.1)
if episode > 480:
time.sleep(0.5)
# 刷新环境状态 , 使得screen 可以联系的动
env.render() # 显示新位置
# 根据 输入的环境特征s 输出选择动作 a
action = model.choose_action(state, epsilon) # 根据状态选择行为
# 通过当前选择的动作得到,执行这个动作后的结果也就是,下一步状态s_(也就是observation) 特征值矩阵 ,
# 立即回报r 返回动作执行的奖励 , r是一个float类型
# 终止状态 done (done=True时环境结束) , done 是 bool
# 调试信息 info (一般没用)
# 环境根据行为给出下一个状态,奖励,是否结束。
next_state, reward, terminal = env.step(action) # env.step(a) 是执行 a 动作
# state = [-0.5 - 0.5] action = 1 reward = 0 next_state = [-0.5 - 0.25] terminal = False
# print("episode=", episode,"step=", step_every_episode, "state=", state, "action=", action, "reward=", reward, "next_state=", next_state, "terminal=", terminal)
# 到这里,预测流程就结束........
# 存储数据
# 每完成一个动作,记忆存储数据一次
model.store_transition(state, action, reward, next_state) # 模型存储经历
# 按批更新
# 假如我们总训练2000次,
# 在训练第i_episode(200)次后,我们数据库中累计的信息超过3000条后。
# 这个时 dqn中的数据库中的记忆条数 大于 数据库的容量
# 控制学习起始时间(先积累记忆再学习)和控制学习的频率(积累多少步经验学习一次)
if step > 200 and step % 5 == 0:
# 它就会开对去学习。
# eval 每学一次就会更新一次 # 它的更新思路是从我历史记忆中随机抽取数据。 #学习一次,就在数据库中随机挑选BATCH_SIZE(32条) 进行打包
# 而target不一样,它是在我们学习过程中到一定频率(TARGET_REPLACE_ITER,来决定)。它的思路是:target网会去复制eval网的参数
model.learn()
# env判断游戏没有结束进行while循环,下次状态变成当前状态, 开始走下一步。
state = next_state # 当前状态
# 在满足 大于数据库容量的条件下,我再看env.step(a) 返回的done,env是否认为实验结束了
# 状态是否为终止
if terminal:
print("episode=", episode, end=",") # 第几轮
print("step=", step_every_episode) # 第几步
model.steps_of_each_episode.append(step_every_episode) # 记录每轮走的步数
break
step += 1 # 总步数+1
step_every_episode += 1 # 当前轮的步数+1
# 游戏环境结束
print("====Game Over====")
env.destroy()
if __name__ == "__main__":
env = Maze() # 环境
# 实例化DQN类,也就是实例化这个强化学习网络
model = DQN(
n_states=env.n_states, # 状态空间个数
n_actions=env.n_actions # 动作空间个数
) # 算法模型
run_maze() # 训练
env.mainloop() # mainloop()方法允许程序循环执行,并进入等待和处理事件
model.plot_cost() # 画误差曲线
model.plot_steps_of_each_episode() # 画每轮走的步数
2. maze_env.py
import tkinter as tk
import sys
import numpy as np
UNIT = 40 # pixels 像素
MAZE_H = 4 # grid height y轴格子数
MAZE_W = 4 # grid width x格子数
# 迷宫
class Maze(tk.Tk, object):
def __init__(self):
print("<env init>")
super(Maze, self).__init__()
# 动作空间(定义智能体可选的行为),action=0-3
self.action_space = ['u', 'd', 'l', 'r']
# 使用变量
self.n_actions = len(self.action_space)
# 状态空间,state=0,1
self.n_states = 2
# 配置信息
self.title('maze')
# 设置屏幕大小
self.geometry("160x160")
# 初始化操作
self.__build_maze()
# 渲染画面
def render(self):
# time.sleep(0.1)
self.update()
# 重置环境
def reset(self):
# 智能体回到初始位置
# time.sleep(0.1)
self.update()
self.canvas.delete(self.rect)
origin = np.array([20, 20])
# 智能体位置,前两个左上角坐标(x0,y0),后两个右下角坐标(x1,y1)
self.rect = self.canvas.create_rectangle(
origin[0] - 15, origin[1] - 15,
origin[0] + 15, origin[1] + 15,
fill='red')
# return observation 状态
# canvas.coords(长方形/椭圆),会得到 【左极值点、上极值点、右极值点、下极值点】这四个点组成的元组,:2表示前2个
return (np.array(self.canvas.coords(self.rect)[:2]) - np.array(self.canvas.coords(self.oval)[:2])) / (MAZE_H * UNIT)
# 智能体向前移动一步:返回next_state,reward,terminal
def step(self, action):
s = self.canvas.coords(self.rect)
base_action = np.array([0, 0])
if action == 0: # up
if s[1] > UNIT:
base_action[1] -= UNIT
elif action == 1: # down
if s[1] < (MAZE_H - 1) * UNIT:
base_action[1] += UNIT
elif action == 2: # right
if s[0] < (MAZE_W - 1) * UNIT:
base_action[0] += UNIT
elif action == 3: # left
if s[0] > UNIT:
base_action[0] -= UNIT
self.canvas.move(self.rect, base_action[0], base_action[1]) # move agent
next_coords = self.canvas.coords(self.rect) # next state
# reward function
if next_coords == self.canvas.coords(self.oval):
reward = 1
print("victory")
done = True
elif next_coords in [self.canvas.coords(self.hell1)]:
reward = -1
print("defeat")
done = True
else:
reward = 0
done = False
s_ = (np.array(next_coords[:2]) - np.array(self.canvas.coords(self.oval)[:2])) / (MAZE_H * UNIT)
return s_, reward, done
def __build_maze(self):
self.canvas = tk.Canvas(self, bg='white',
height=MAZE_H * UNIT,
width=MAZE_W * UNIT)
# create grids
for c in range(0, MAZE_W * UNIT, UNIT):
x0, y0, x1, y1 = c, 0, c, MAZE_H * UNIT
self.canvas.create_line(x0, y0, x1, y1)
for r in range(0, MAZE_H * UNIT, UNIT):
x0, y0, x1, y1 = 0, r, MAZE_W * UNIT, r
self.canvas.create_line(x0, y0, x1, y1)
origin = np.array([20, 20])
hell1_center = origin + np.array([UNIT * 2, UNIT])
# 陷阱
self.hell1 = self.canvas.create_rectangle(
hell1_center[0] - 15, hell1_center[1] - 15,
hell1_center[0] + 15, hell1_center[1] + 15,
fill='black')
oval_center = origin + UNIT * 2
# 出口
self.oval = self.canvas.create_oval(
oval_center[0] - 15, oval_center[1] - 15,
oval_center[0] + 15, oval_center[1] + 15,
fill='yellow')
# 智能体
self.rect = self.canvas.create_rectangle(
origin[0] - 15, origin[1] - 15,
origin[0] + 15, origin[1] + 15,
fill='red')
self.canvas.pack()
3.RL_brain.py
import torch
import torch.nn as nn
import numpy as np
import torch.nn.functional as F
import matplotlib.pyplot as plt
# 深度网络,全连接层
class Net(nn.Module):
def __init__(self, n_states, n_actions):
super(Net, self).__init__()
# n_states状态个数
self.fc1 = nn.Linear(n_states, 10)
# n_actions动作个数
self.fc2 = nn.Linear(10, n_actions)
self.fc1.weight.data.normal_(0, 0.1) # 初始化权重,用二值分布来随机生成参数的值
self.fc2.weight.data.normal_(0, 0.1)
# 前向传播
def forward(self, x):
# 这里以一个动作为作为观测值进行输入,然后把他们输出给10个神经元
x = self.fc1(x)
# 激活函数
x = F.relu(x)
# 经过10个神经元运算过后的数据, 把每个动作的价值作为输出。
out = self.fc2(x)
return out
# 定义DQN 网络class
class DQN:
# n_states 状态空间个数;n_actions 动作空间大小
def __init__(self, n_states, n_actions):
print("<DQN init> n_states=", n_states, "n_actions=", n_actions)
# 建立一个评估网络(eval) 和 Q现实网络 (target)
# DQN有两个net:target net和eval net,具有选动作,存经历,学习三个基本功能
self.eval_net, self.target_net = Net(n_states, n_actions), Net(n_states, n_actions)
# 损失函数
self.loss = nn.MSELoss()
# 优化器,优化评估神经网络(仅优化eval)
self.optimizer = torch.optim.Adam(self.eval_net.parameters(), lr=0.01)
self.n_actions = n_actions # 状态空间个数
self.n_states = n_states # 动作空间大小
# 使用变量
# 用来记录学习到第几步了
self.learn_step_counter = 0 # target网络学习计数
# 用来记录当前指到数据库的第几个数据了
self.memory_counter = 0 # 记忆计数
# MEMORY_CAPACITY = 2000 , 限制了数据库只能记住2000个。前面的会被后面的覆盖
# 一次存储的数据量有多大 MEMORY_CAPACITY 确定了memory数据库有多大 ,
# 后面的 N_STATES * 2 + 2 是因为 两个 N_STATES(在这里是4格子,因为N_STATES就为4) + 一个 action动作(1格) + 一个 rward(奖励)
self.memory = np.zeros((2000, 2 * 2 + 2)) # 2*2(state和next_state,每个x,y坐标确定)+2(action和reward),存储2000个记忆体
self.cost = [] # 记录损失值
self.steps_of_each_episode = [] # 记录每轮走的步数
# 进行选择动作
# x是state= [-0.5 -0.5]
def choose_action(self, x, epsilon):
#print("<choose_action> x=", x, "torch.FloatTensor(x)=", torch.FloatTensor(x))
# 获取输入
# torch.unsqueeze(input, dim) → Tensor unsqueeze()函数起升维的作用,参数dim表示在哪个地方加一个维度,注意dim范围在:[-input.dim() - 1, input.dim() + 1]之间,比如输入input是一维,则dim=0时数据为行方向扩,dim=1时为列方向扩,再大错误。
# torch.FloatTensor(x)= tensor([-0.5000, -0.5000])
# 扩展一行,因为网络是多维矩阵,输入是至少两维
x = torch.unsqueeze(torch.FloatTensor(x), 0)
# tensor([[-0.5000, -0.5000]])
#print("<choose_action> x=", x, "epsilon=", epsilon)
# 在大部分情况,我们选择 去max-value
if np.random.uniform() < epsilon: # greedy # 随机结果是否大于EPSILON(0.9)
action_value = self.eval_net.forward(x)
# torch.max() 返回输入张量所有元素的最大值,torch.max(input, dim),dim是max函数索引的维度0/1,0是每列的最大值,1是每行的最大值
# torch.max(a, 1)[1] 代表a中每行最大值的索引
# .data.numpy()[0]将Variable转换成tensor
# 哪个神经元值最大,则代表下一个动作
action = torch.max(action_value, 1)[1].data.numpy()[0]
# <choose_action> action_value= tensor([[-0.2394, -0.3109, -0.3330, -0.0376]], grad_fn=<AddmmBackward0>) torch.max(action_value, 1)= torch.return_types.max(values=tensor([-0.0376], grad_fn=<MaxBackward0>), indices=tensor([3])) torch.max(action_value, 1)[1]= tensor([3]) action= 3
# print("<choose_action> action_value=", action_value, "torch.max(action_value, 1)=",torch.max(action_value, 1),"torch.max(action_value, 1)[1]=",torch.max(action_value, 1)[1], "action=", action)
# 在少部分情况,我们选择 随机选择 (变异)
else:
# random.randint(参数1,参数2)函数用于生成参数1和参数2之间的任意整数,参数1 <= n < 参数2
action = np.random.randint(0, self.n_actions)
# print("action=", action)
return action
# 存储数据
# 本次状态,执行的动作,获得的奖励分, 完成动作后产生的下一个状态。
# 存储这四个值
def store_transition(self, state, action, reward, next_state):
# 把所有的记忆捆在一起,以 np类型
# 把 三个矩阵 s ,[a,r] ,s_ 平铺在一行 [a,r]是因为 他们都是 int 没有 [] 就无法平铺 ,并不代表把他们捆在一起了
# np.vstack()是把矩阵进行列连接
transition = np.hstack((state, [action, reward], next_state))
# state= [0.25 0. ] action= 3 reward= 1 next_state= [0. 0.]
# <store_transition> transition= [0.25 0. 3. 1. 0. 0. ]
#print("<store_transition> transition=", transition)
# index 是 这一次录入的数据在 MEMORY_CAPACITY 的哪一个位置
index = self.memory_counter % 200 # 满了就覆盖旧的
# 如果,记忆超过上线,我们重新索引。即覆盖老的记忆。
self.memory[index, :] = transition # 将transition添加为memory的一行
#print("<store_transition> memory=", self.memory)
self.memory_counter += 1
# 从存储学习数据
# target 是 达到次数后更新, eval net是 每次learn 就进行更新
def learn(self):
# print("<learn>")
# target net 更新频率,用于预测,不会及时更新参数
# target parameter update 是否要更新现实网络
# target Q现实网络 要间隔多少步跟新一下。 如果learn步数 达到 TARGET_REPLACE_ITER 就进行一次更新
if self.learn_step_counter % 100 == 0:
# 把最新的eval 预测网络 推 给target Q现实网络
# 也就是变成,还未变化的eval网
self.target_net.load_state_dict((self.eval_net.state_dict()))
# 'fc1.weight', 'fc1.bias', 'fc2.weight', ....
#print("<learn> eval_net.state_dict()=", (self.eval_net.state_dict()))
self.learn_step_counter += 1
# eval net是 每次learn 就进行更新
# 更新逻辑就是从记忆库中随机抽取BATCH_SIZE个(32个)数据。
# 使用记忆库中批量数据
# sample_index = np.random.choice(MEMORY_CAPACITY, BATCH_SIZE) # 从 数据库中 随机 抽取 BATCH_SIZE条数据
sample_index = np.random.choice(200, 16) # 200个中随机抽取16个作为batch_size
# sample_index= [ 34 48 153 60 5 140 74 81 93 85 138 33 118 90 11 124]
# print("<learn> sample_index=", sample_index)
memory = self.memory[sample_index, :] # 抽取BATCH_SIZE个(16个)个记忆单元, 把这BATCH_SIZE个(16个)数据打包.
# memory= [[-0.5 -0.25 1. 0. -0.5 0. ]
# [-0.5 0.25 1. 0. -0.5 0.25]
# [ 0. 0.25 2. 0. 0.25 0.25]
# ...]
# print("<learn> memory=", memory)
state = torch.FloatTensor(memory[:, :2]) # # 32个记忆的包,包里是(当时的状态) 所有行里取0,1
# 下面这些变量是 32个数据打包的变量
# state= tensor([[-0.5000, -0.2500],
# [-0.5000, 0.2500],
# [ 0.0000, 0.2500],
# ...]
# print("<learn> state=", state)
action = torch.LongTensor(memory[:, 2:3]) # # 32个记忆的包,包里是(当时做出的动作)2
# action= tensor([[1],
# [1],
# [2],
# ...]
# print("<learn> action=", action)
reward = torch.LongTensor(memory[:, 3:4]) # # 32个记忆的包,包里是 (当初获得的奖励)3
next_state = torch.FloatTensor(memory[:, 4:6]) # 32个记忆的包,包里是 (执行动作后,下一个动作的状态)4,5
# q_eval w.r.t the action in experience
# q_eval的学习过程
# self.eval_net(state).gather(1, action) 输入我们包(32条)中的所有状态 并得到(32条)所有状态的所有动作价值,
# .gather(1,action) 只取这32个状态中 的 每一个状态的最大值
# 预期价值计算 == 随机32条数据中的最大值
# 计算loss,
# q_eval:所采取动作的预测value,
# q_target:所采取动作的实际value
# a.gather(0, b)分为3个部分,a是需要被提取元素的矩阵,0代表的是提取的维度为0,b是提取元素的索引。
# 当前状态的预测:
# 输入现在的状态state,通过forward()生成所有动作的价值,根据价值选取动作,把它的价值赋值给q_eval
q_eval = self.eval_net(state).gather(1, action) # eval_net->(64,4)->按照action索引提取出q_value
# state= tensor([[-0.2500, -0.2500],
# [-0.2500, -0.2500],
# [-0.5000, -0.5000],
# ...]
# eval_net(state)= tensor([[-0.1895, -0.2704, -0.3506, -0.3678],
# [-0.1895, -0.2704, -0.3506, -0.3678],
# [-0.2065, -0.2666, -0.3501, -0.3738],
# ...]
# action= tensor([[0],
# [1],
# [0],
# ...]
# q_eval= tensor([[-0.1895],
# [-0.2704],
# [-0.2065],
# ...]
# print("<learn> eval_net(state)=", self.eval_net(state), "q_eval=", q_eval)
# 下一步状态的预测:
# 计算最大价值的动作:输入下一个状态 进入我们的现实网络 输出下一个动作的价值 .detach() 阻止网络反向传递,我们的target需要自己定义该如何更新,它的更新在learn那一步
# 把target网络中下一步的状态对应的价值赋值给q_next;此处有时会反向传播更新target,但此处不需更新,故加.detach()
q_next = self.target_net(next_state).detach() # detach from graph, don't backpropagate
# 计算对于的最大价值
# q_target 实际价值的计算 == 当前价值 + GAMMA(未来价值递减参数) * 未来的价值
# max函数返回索引加最大值,索引是1最大值是0 torch.max->[values=[],indices=[]] max(1)[0]->values=[]
q_target = reward + 0.9 * q_next.max(1)[0].unsqueeze(1) # label # shape (batch, 1)
# q_next= tensor([[-0.1943, -0.2676, -0.3566, -0.3752],
# [-0.1848, -0.2731, -0.3446, -0.3604],
# [-0.2065, -0.2666, -0.3501, -0.3738],
# ...]
# q_next.max(1)= torch.return_types.max(values=tensor([-0.1943, -0.1848, -0.2065,...]), indices=tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]))
# q_next.max(1)[0]= tensor([-0.1943, -0.1848, -0.2065,....])
# q_next.max(1)[0].unsqueeze(1)= tensor([[-0.1943], [-0.1848], [-0.2065],...])
# q_target= tensor([[-0.1749],
# [-0.1663],
# [-0.1859],
# ...]
# print("<learn> q_target=", q_target, "q_next=", q_next, "q_next.max(1)=", q_next.max(1), "q_next.max(1)[0]=", q_next.max(1)[0], "q_next.max(1)[0].unsqueeze(1)=", q_next.max(1)[0].unsqueeze(1))
# 通过预测值与真实值计算损失 q_eval预测值, q_target真实值
loss = self.loss(q_eval, q_target)
self.cost.append(loss.detach().numpy())
# 根据误差,去优化我们eval网, 因为这是eval的优化器
# 反向传递误差,进行参数更新
self.optimizer.zero_grad() # 梯度重置
loss.backward() # 反向求导
self.optimizer.step() # 更新模型参数
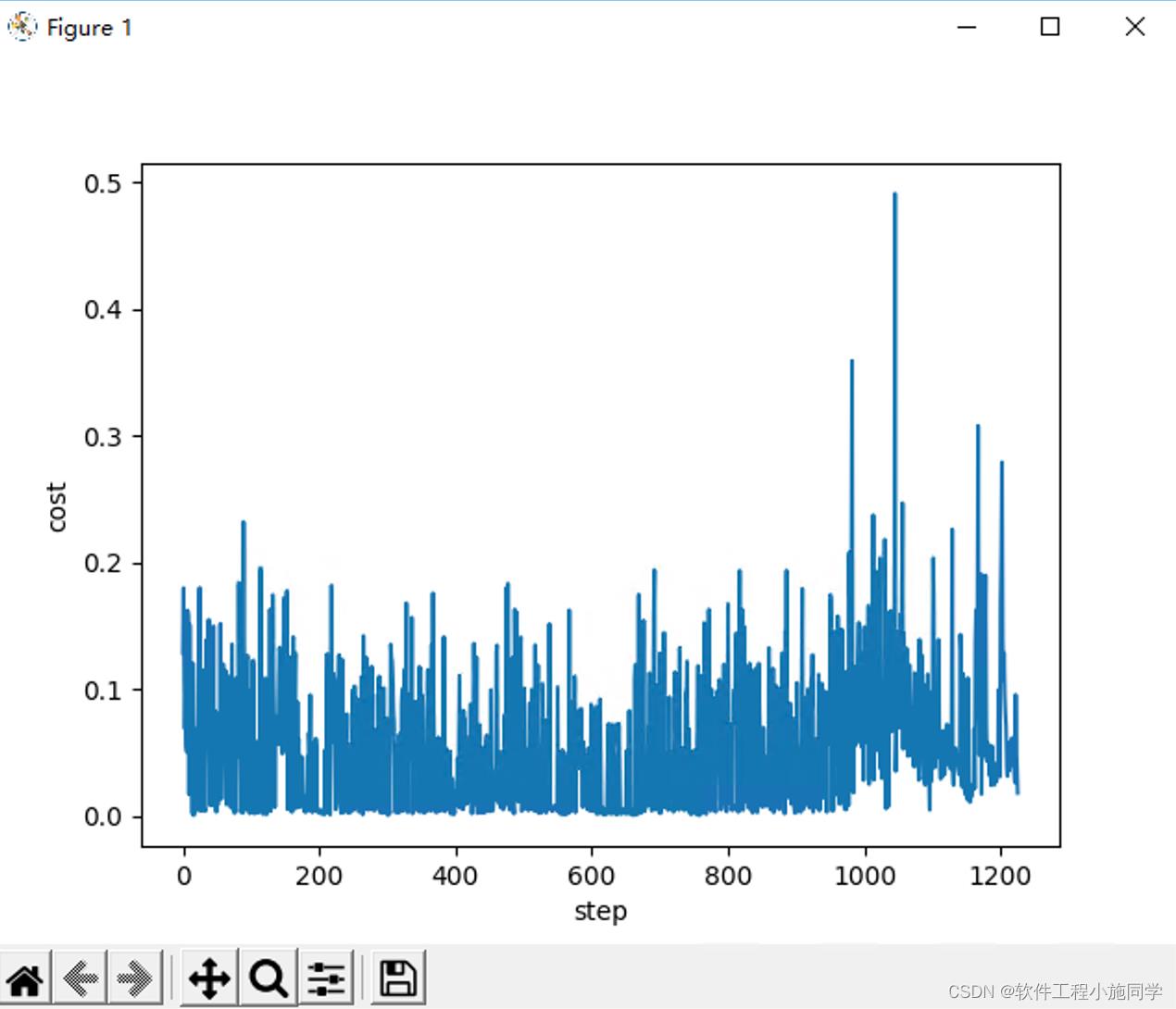
# 绘制损失图
def plot_cost(self):
# loss = self.loss(q_eval, q_target)
# self.cost.append(loss)
# np.arange(3)产生0-2数组
plt.plot(np.arange(len(self.cost)), self.cost)
plt.xlabel("step")
plt.ylabel("cost")
plt.show()
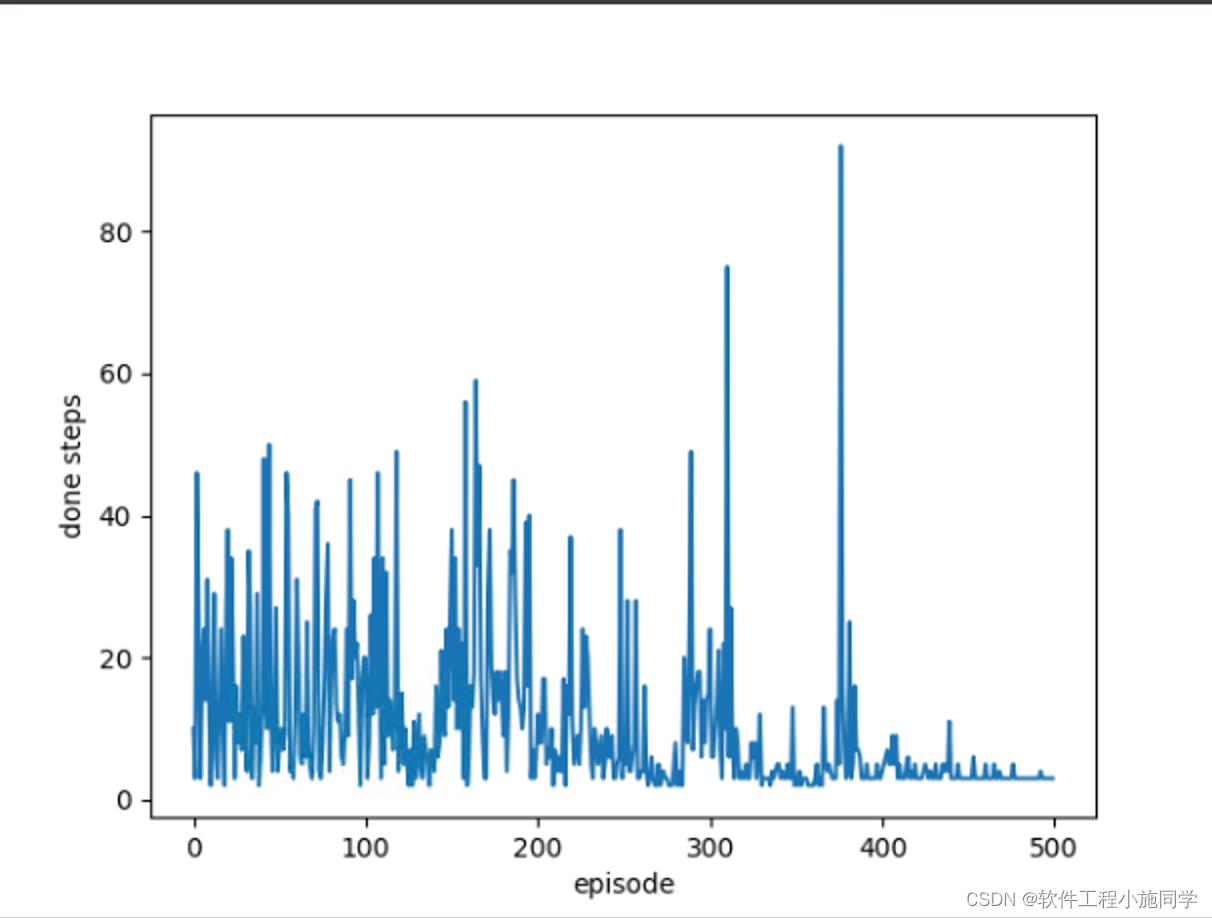
# 绘制每轮需要走几步
def plot_steps_of_each_episode(self):
plt.plot(np.arange(len(self.steps_of_each_episode)), self.steps_of_each_episode)
plt.xlabel("episode")
plt.ylabel("done steps")
plt.show()
原文:
DQN - Sunshine_y - 博客园DQN简介 DQN,全称Deep Q Network,是一种融合了神经网络和Q-learning的方法。这种新型结构突破了传统强化学习的瓶颈,下面具体介绍: 神经网络的作用 传统强化学习使用表格形式来https://www.cnblogs.com/TzySec/p/15638979.html强化学习算法实例DQN代码PyTorch实现 - -Rocky- - 博客园前言 实例参考MorvanZhou/Reinforcement-learning-with-tensorflow, 更改为PyTorch实现,并增加了几处优化。实现效果如下。 其中,红色方块作为探索的
https://www.cnblogs.com/nrocky/p/14496252.html
以上是关于强化学习 DQN pytorch实例的主要内容,如果未能解决你的问题,请参考以下文章
 https://mofanpy.com/tutorials/machine-learning/reinforcement-learning/DQN2
https://mofanpy.com/tutorials/machine-learning/reinforcement-learning/DQN2