局部模型无关方法

Posted 2023-01-09 上下求索.

第9章 局部模型无关方法

局部解释方法解释个别预测。在本章中，你将了解以下局部解释方法：

• 单个条件期望曲线是部分依赖图的构建块，描述了改变特征如何改变预测。
• 局部代理模型（LIME）通过将复杂模型替换为局部可解释的代理模型来解释预测。
• 范围规则（锚点）是描述哪些特征值锚定预测的规则，从某种意义上说，它们将预测锁定到位。
• 反事实解释通过检查需要更改哪些特征以实现所需的预测来解释预测。
• Shapley 值是一种归因方法，可以将预测公平地分配给各个特征。
• SHAP是 Shapley 值的另一种计算方法，但也提出了基于数据中 Shapley 值组合的全局解释方法。

LIME 和 Shapley 值是归因方法，因此单个实​​例的预测被描述为特征效应的总和。其他方法，例如反事实解释，是基于示例的。

9.1 个人条件期望

单个条件期望 (ICE) 图在每个实例中显示一条线，显示当特征发生变化时实例的预测如何变化。

特征平均效果的部分依赖图是一种全局方法，因为它不关注特定实例，而是关注整体平均值。对应于单个数据实例的 PDP 被称为单个条件期望 (ICE) 图 (Goldstein et al. 2017¹)。ICE 图可视化了预测对每个特征的依赖性单独实例，导致每个实例一条线，而部分依赖图中的一条线整体。PDP 是 ICE 图线的平均值。可以通过保持所有其他特征相同来计算一条线（和一个实例）的值，通过将特征的值替换为网格中的值并使用黑盒模型对这些新创建的实例进行预测来创建该实例的变体。结果是具有来自网格的特征值和相应预测的实例的一组点。

关注个人期望而不是部分依赖有什么意义？部分依赖图可以掩盖由交互作用产生的异质关系。PDP 可以向你展示特征与预测之间的平均关系是什么样的。这仅在计算 PDP 的特征与其他特征之间的相互作用较弱时才有效。在交互的情况下，ICE 图将提供更多的洞察力。

更正式的定义：在 ICE 图中，对于每个实例 $(x_S^{(i)},x_C^{(i)}){}_{i=1}^N$ ， $x_S^{(i)}$ 对应的曲线 ${\hat{f}}_S^{(i)}$ 都会重绘，$x_C^{(i)}$ 则固定不变.

9.1.1 示例

让我们回到宫颈癌数据集，看看每个实例的预测如何与特征“年龄”相关联。我们将分析一个随机森林，该森林预测给定风险因素的女性患癌症的概率。

在部分依赖图中，我们看到癌症概率在 50 岁左右增加，但对于数据集中的每个女性来说都是如此吗？ICE 图显示，对于大多数女性而言，年龄效应遵循 50 岁时增加的平均模式，但也有一些例外：对于在年轻时预测概率较高的少数女性，预测的癌症概率不会改变随着年龄的增长。

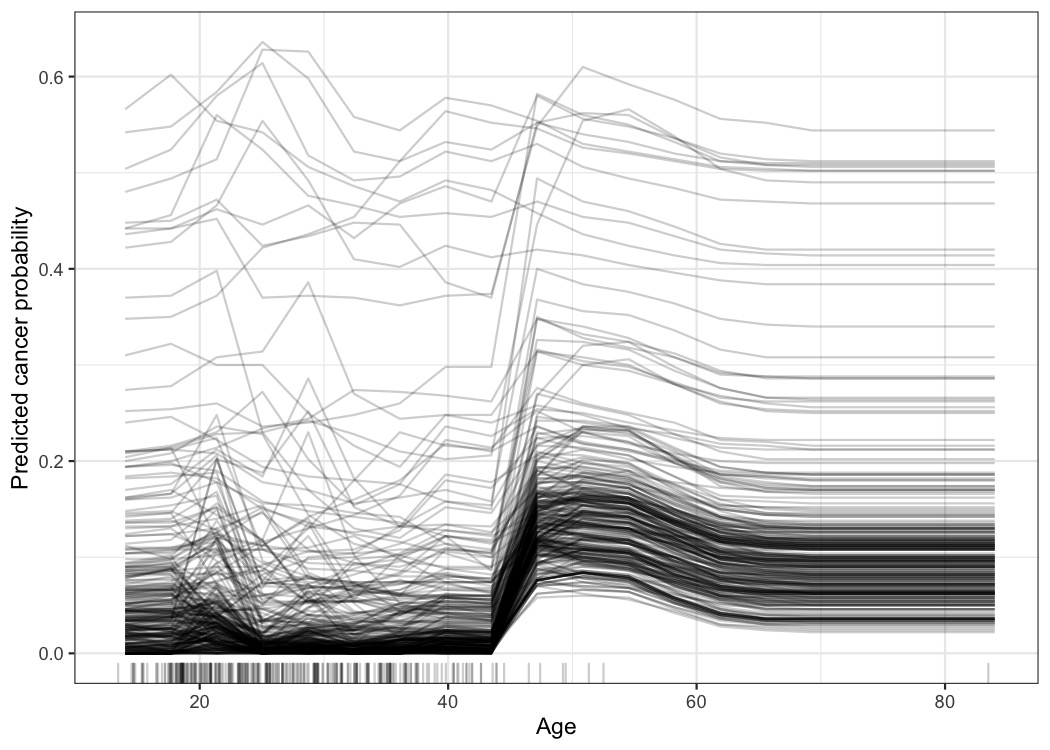
图 9.1：按年龄划分的宫颈癌概率 ICE 图。每条线代表一个女人。对于大多数女性来说，随着年龄的增长，预测的癌症概率会增加。对于一些预测癌症概率高于 0.4 的女性，预测在较高年龄时变化不大。

下图显示了自行车租赁预测的 ICE 图。底层预测模型是随机森林。

The next figure shows ICE plots for the bike rental prediction.
The underlying prediction model is a random forest.

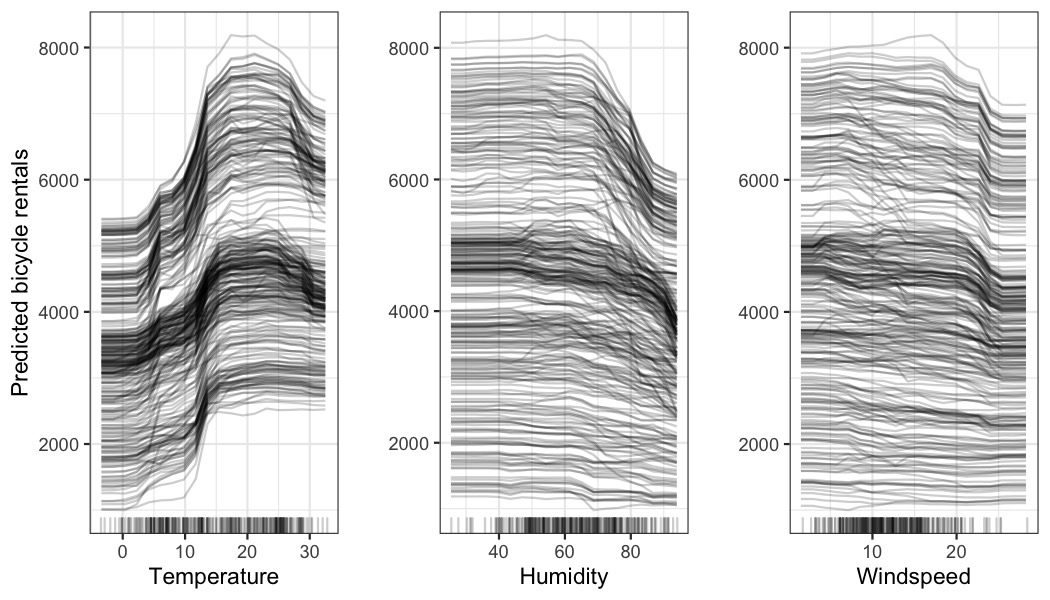
所有曲线似乎都遵循相同的路线，因此没有明显的相互作用。这意味着 PDP 已经很好地总结了显示的特征和预测的自行车数量之间的关系。

9.1.1.1 居中的 ICE 图

ICE 图有一个问题：有时很难判断个体之间的 ICE 曲线是否不同，因为它们开始于不同的预测。一个简单的解决方案是将曲线在特征中的某个点居中，并仅显示与该点的预测差异。生成的图称为居中 ICE 图 (c-ICE)。将曲线锚定在特征的下端是一个不错的选择。新曲线定义为：

$${\hat{f}}_{cent}^{(i)}={\hat{f}}^{(i)}-1\hat{f}(x^a,x_C^{(i)})$$

在哪里 $1$ 是具有适当维数（通常为1或2）的 1 向量， $\hat{f}$ 是拟合模型，$x^a$ 是锚点。

9.1.1.2 示例

例如，以宫颈癌 ICE 的年龄图为例，以观察到的最年轻的年龄为中心：

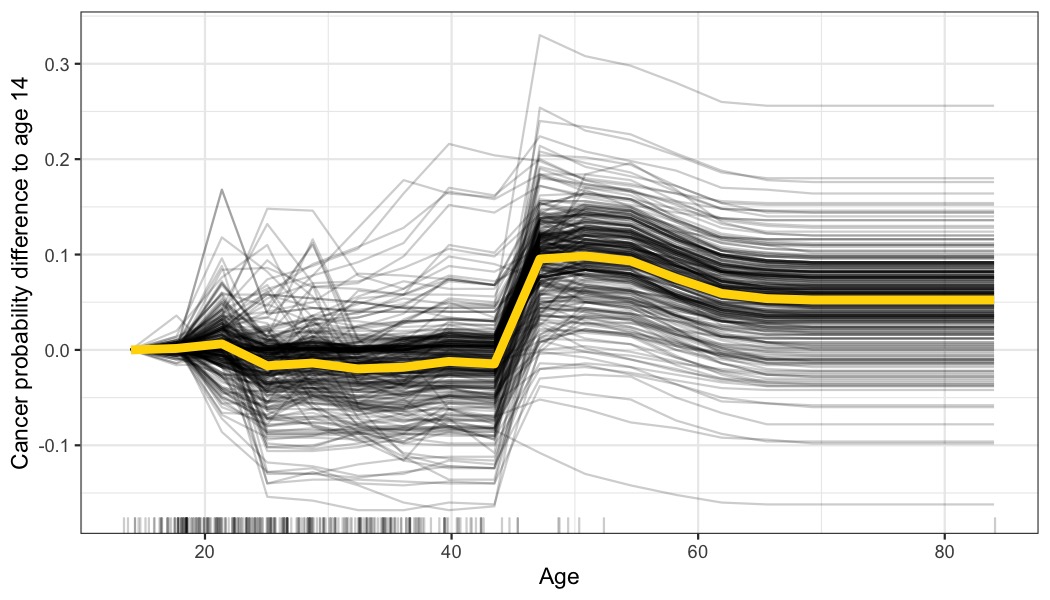
图 9.3：按年龄预测的癌症概率的中心 ICE 图。线在 14 岁时固定为 0。与 14 岁相比，大多数女性的预测保持不变，直到 45 岁时预测概率增加。

居中的 ICE 图便于比较各个实例的曲线。如果我们不想看到预测值的绝对变化，而是希望看到预测与特征范围的固定点相比的差异，这可能很有用。

让我们看一下自行车租赁预测的居中 ICE 图：

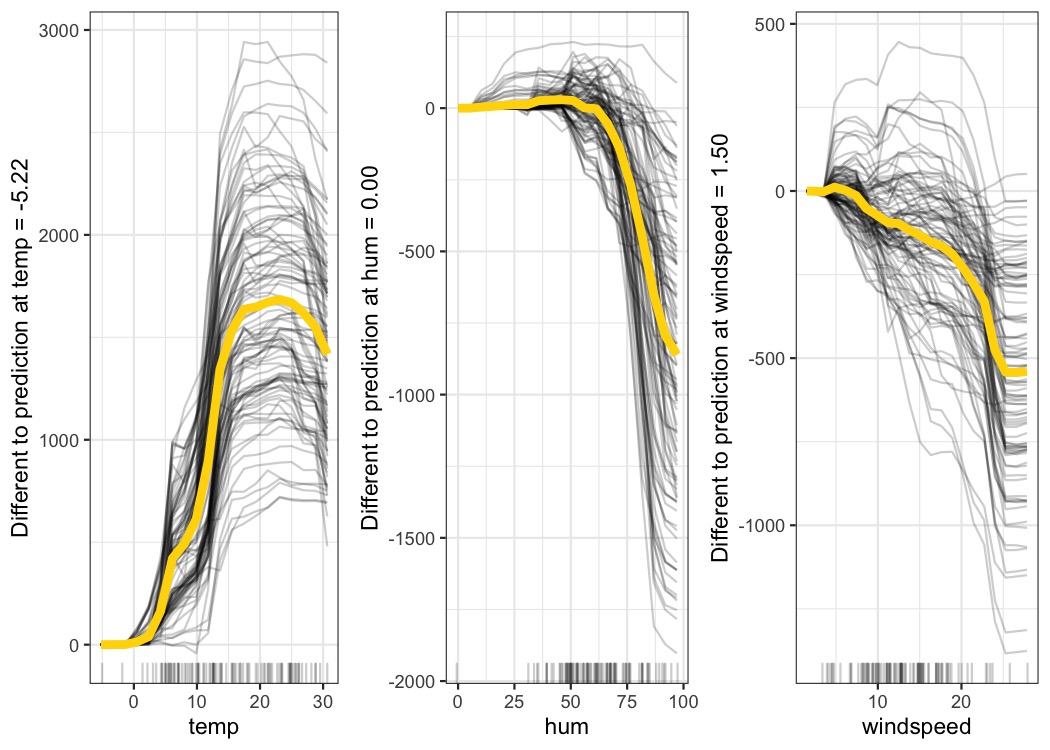
图 9.4：按天气条件预测的自行车数量的居中 ICE 图。这些线显示了预测与相应特征值处于观察到的最小值的预测相比的差异。

9.1.1.3 导数 ICE 图

另一种在视觉上更容易发现异质性的方法是查看预测函数相对于特征的各个导数。生成的图称为导数 ICE 图 (d-ICE)。函数（或曲线）的导数告诉你变化是否发生以及发生的方向。使用导数 ICE 图，很容易发现黑盒预测对于（至少某些）实例发生变化的特征值范围。如果分析的特征 $x_S$ 和其他特征 $x_C$ 之间没有交互，则预测函数可表示为：

$$\hat{f}(x)=\hat{f}(x_S,x_C)=g(x_S)+h(x_C),\text{with}\frac{\delta \hat{f}(x)}{\delta x_S}=g^{\prime }(x_S)$$

在没有交互作用的情况下，所有实例的各个偏导数应该是相同的。如果它们不同，那是由于相互作用，它在 d-ICE 图中变得可见。除了显示预测函数相对于 S 中特征的导数的各个曲线外，显示导数的标准差有助于突出 S 中特征中估计导数存在异质性的区域。导数 ICE 图需要很长时间来计算并且相当不切实际。

9.1.2 优势

单个条件期望曲线比部分依赖图更易于理解。如果我们改变感兴趣的特征，一条线代表一个实例的预测。与部分依赖图不同，ICE 曲线可以揭示异质关系。

9.1.3 缺点

ICE 曲线只能显示一个特征，因为两个特征需要绘制多个重叠表面，而你在图中看不到任何东西。

ICE 曲线面临与 PDP 相同的问题：如果感兴趣的特征与其他特征相关，那么根据联合特征分布，线条中的某些点可能是无效数据点。

如果绘制了许多 ICE 曲线，绘图可能会变得过于拥挤，你将看不到任何东西。解决方案：要么为线条添加一些透明度，要么只绘制线条的样本。

在 ICE 图中，可能不容易看到平均值。这有一个简单的解决方案：将单个条件期望曲线与部分依赖图结合起来。

9.1.4 软件和替代品

ICE 图在 R 包iml（用于这些示例）、ICEbox²和 pdp. 另一个与 ICE 非常相似的 R 包是 condvis 。 在 Python 中，部分依赖图从 0.24.0 版本开始内置到 scikit-learn 中。

9.2 本地代理（LIME）

局部代理模型是可解释的模型，用于解释黑盒机器学习模型的个别预测。本地可解释模型不可知论解释 (LIME) 50是一篇论文，其中作者提出了本地代理模型的具体实现。代理模型被训练以近似底层黑盒模型的预测。LIME 没有训练全局代理模型，而是专注于训练局部代理模型来解释个体预测。

这个想法非常直观。首先，忘记训练数据，想象你只有一个黑盒模型，你可以在其中输入数据点并获得模型的预测。你可以随心所欲地探测盒子。你的目标是了解机器学习模型为何做出某种预测。LIME 测试当你将数据的变化提供给机器学习模型时预测会发生什么。LIME 生成一个由扰动样本和黑盒模型的相应预测组成的新数据集。然后在这个新数据集上，LIME 训练一个可解释的模型，该模型由采样实例与感兴趣实例的接近程度加权。可解释模型可以是可解释模型章节中的任何内容，例如Lasso或决策树。学习模型应该是机器学习模型局部预测的良好近似，但不一定是良好的全局近似。这种精度也称为局部保真度。

在数学上，具有可解释性约束的局部代理模型可以表示如下：

$$\text{explanation}(x)=\arg \underset{g\in G}{\min }L(f,g,{\pi }_x)+\Omega (g)$$

例如 x 的解释模型是最小化损失 L（例如均方误差）的模型 g（例如线性回归模型），它衡量解释与原始模型 f（例如 xgboost 模型）的预测的接近程度，而模型复杂度 $\Omega (g)$ 保持低（例如，喜欢更少的功能）。G 是一系列可能的解释，例如所有可能的线性回归模型。接近度测量 ${\pi }_x$ 定义了我们为解释考虑的实例 $x$ 周围的邻域有多大。在实践中，LIME 只优化了损失部分。用户必须确定复杂性，例如通过选择线性回归模型可以使用的最大特征数。

训练本地代理模型的秘诀：

• 选择你想要解释其黑盒预测的感兴趣的实例。
• 扰动你的数据集并获得这些新点的黑盒预测。
• 根据新样本与感兴趣实例的接近程度对新样本进行加权。
• 在具有变化的数据集上训练一个加权的、可解释的模型。
• 通过解释局部模型来解释预测。

例如，在 R 和 Python 的当前实现中，可以选择线性回归作为可解释的代理模型。事先，你必须选择 K，即你希望在可解释模型中具有的特征数。K 越低，越容易解释模型。更高的 K 可能会产生具有更高保真度的模型。有几种方法可以训练具有恰好 $K$ 个特征的模型。Lasso是一个不错的选择。具有高正则化参数$\lambda$的 Lasso 模型 产生一个没有任何特征的模型。通过重新训练缓慢下降 $\lambda$ 的 Lasso 模型，一个接一个地，特征得到的权重估计值不同于零。如果模型中有 K 个特征，则你已达到所需的特征数量。其他策略是向前或向后选择特征。这意味着你要么从完整模型（等同包含所有特征）开始，要么从仅包含截距的模型开始，然后测试添加或删除哪个特征会带来最大的改进，直到达到具有 K 个特征的模型。

你如何获得数据的变化？这取决于数据的类型，可以是文本、图像或表​​格数据。对于文本和图像，解决方案是打开或关闭单个单词或超像素。在表格数据的情况下，LIME 通过单独扰动每个特征来创建新样本，从特征中提取均值和标准差的正态分布进行绘制。

9.2.1 用于表格数据的 LIME

表格数据是表格中的数据，每一行代表一个实例，每一列代表一个特征。LIME 样本不是围绕感兴趣的实例进行的，而是取自训练数据的质心，这是有问题的。但它增加了某些样本点预测的结果与感兴趣的数据点不同的概率，并且 LIME 至少可以学习一些解释。

最好直观地解释一下采样和局部模型训练的工作原理：

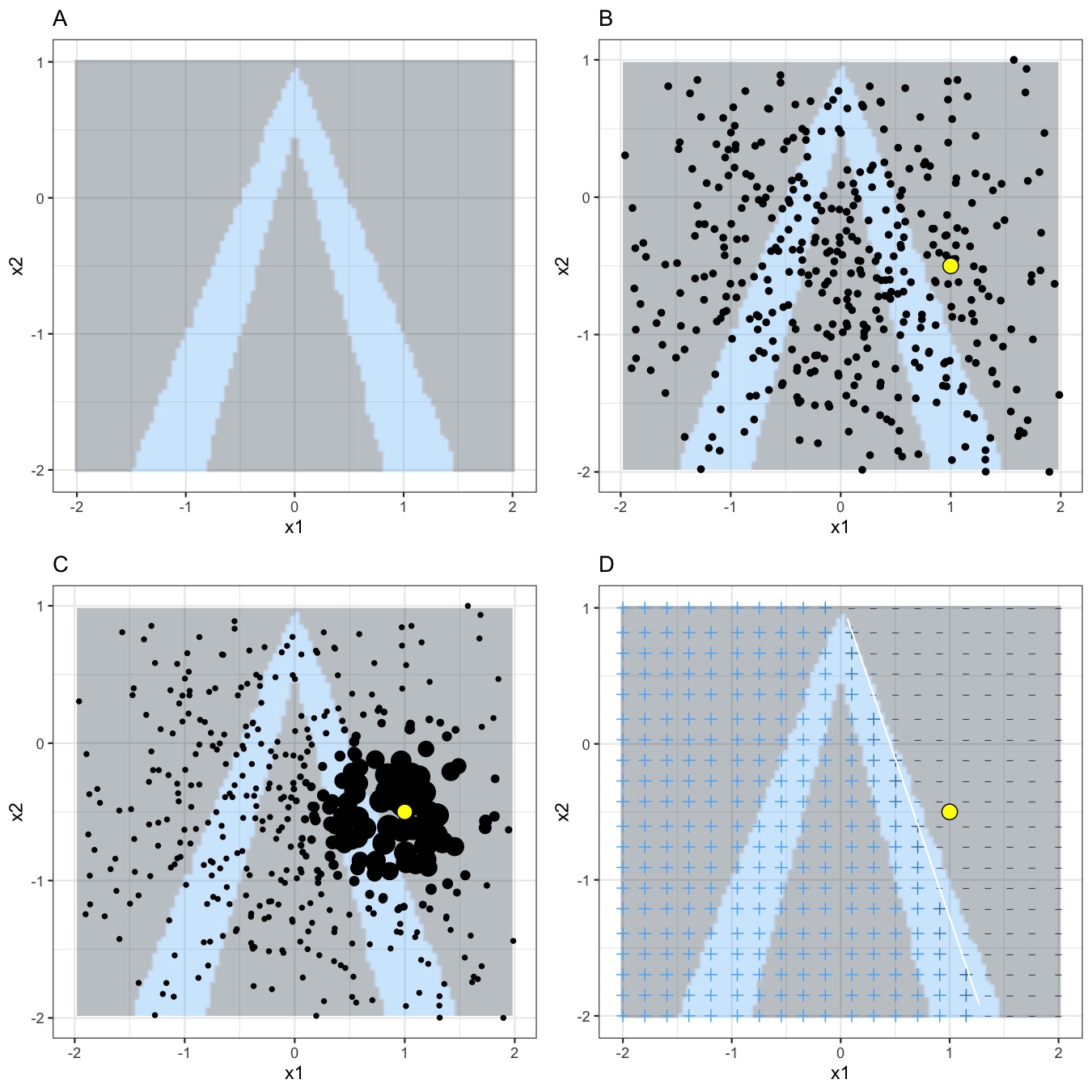
图 9.5：表格数据的 LIME 算法。A) 给定特征 x1 和 x2 的随机森林预测。预测类别：1（暗）或 0（亮）。B) 感兴趣的实例（大点）和从正态分布中采样的数据（小点）。C) 为感兴趣的实例附近的点分配更高的权重。D）网格的符号显示了从加权样本中本地学习模型的分类。白线标记了决策边界（P(class=1) = 0.5）。

一如既往，魔鬼在细节中。围绕一个点定义一个有意义的邻域是很困难的。LIME 目前使用指数平滑核来定义邻域。平滑内核是一个函数，它接受两个数据实例并返回一个邻近度度量。内核宽度决定了邻域的大小：较小的内核宽度意味着实例必须非常接近才能影响局部模型，较大的内核宽度意味着距离较远的实例也会影响模型。如果你查看LIME 的 Python 实现(文件lime/lime_tabular.py)你会看到它使用指数平滑内核（在归一化数据上），内核宽度是训练数据列数平方根的 0.75 倍。它看起来像一行无辜​​的代码，但它就像一头大象坐在客厅里，旁边是你从祖父母那里得到的好瓷器。最大的问题是我们没有找到最佳内核或宽度的好方法。0.75 甚至从何而来？在某些场景下，你可以通过更改内核宽度轻松扭转你的解释，如下图所示：

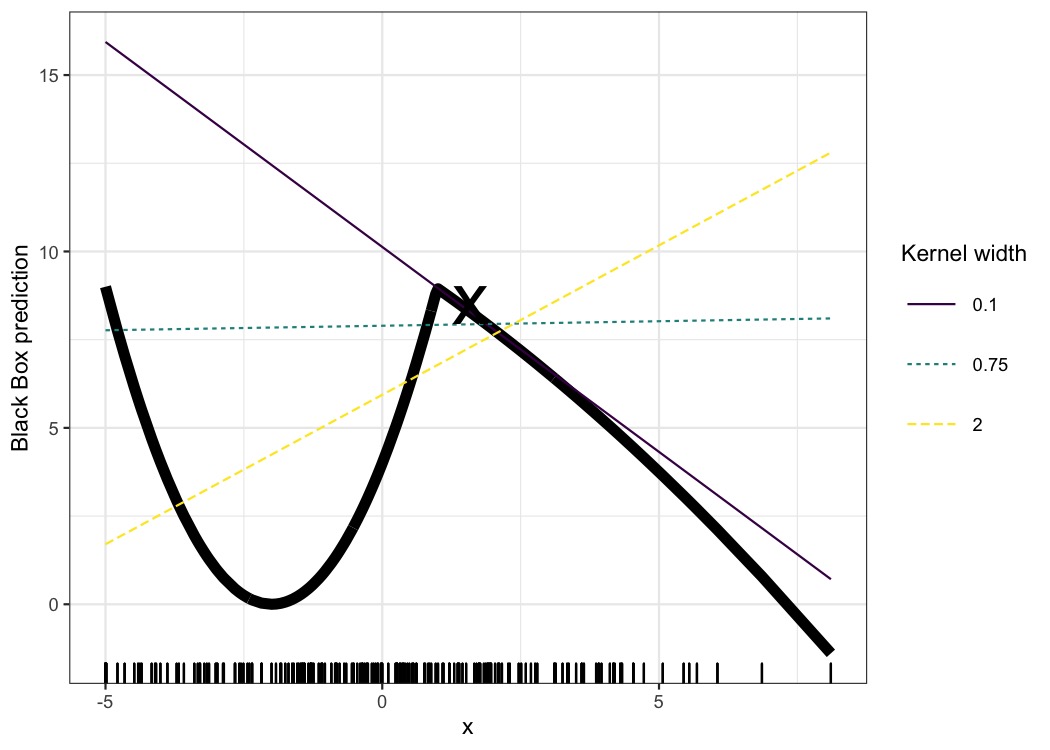
图 9.6：实例 x = 1.6 的预测解释。取决于单个特征的黑盒模型的预测显示为粗线，数据的分布用地毯显​​示。计算了三个具有不同内核宽度的局部代理模型。生成的线性回归模型取决于内核宽度：对于 x = 1.6，该特征是否具有负、正或无影响？

该示例仅显示了一项功能。它在高维特征空间中变得更糟。距离测量是否应该平等地对待所有特征也很不清楚。特征 $x1$ 的距离单位是否与特征 $x2$ 的距离单位相同？距离度量是相当随意的，不同维度（又名特征）的距离可能根本无法比较。

9.2.1.1 示例

让我们看一个具体的例子。我们回到自行车租赁数据，将预测问题转化为一个分类：考虑到自行车租赁随着时间的推移变得越来越流行的趋势后，我们想知道某一天的自行车租赁数量是否会高于或低于趋势线。你也可以将“高于”解释为高于平均自行车数量，但会根据趋势进行调整。

首先，我们在分类任务上用 r ntree 训练一个有 100 棵树的随机森林。根据天气和日历信息，哪一天租用自行车的数量会高于无趋势平均值？

解释是用r n_features_lime个特征创建的。针对具有不同预测类别的两个实例训练的稀疏局部线性模型的结果：

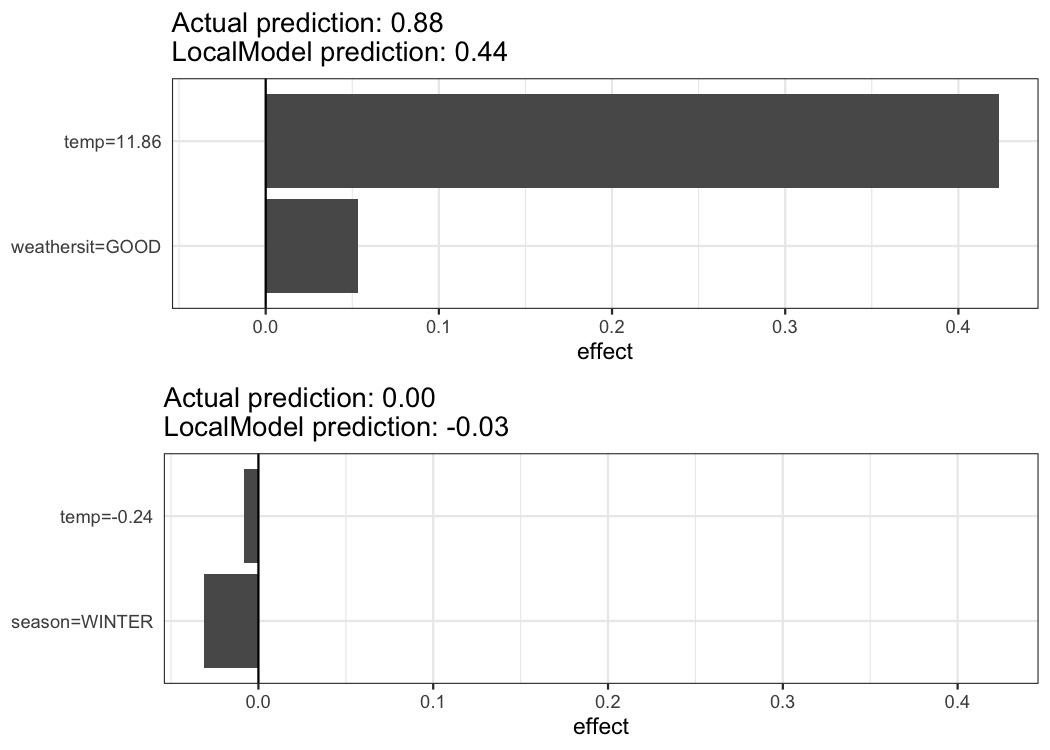
图 9.7：自行车租赁数据集的两个实例的 LIME 解释。气温升高和天气状况良好对预测有积极影响。x 轴显示特征效果：权重乘以实际特征值。

从图中可以清楚地看出，解释分类特征比解释数字特征更容易。一种解决方案是将数值特征分类到 bin 中。

9.2.2 用于文本的 LIME

用于文本的 LIME 与用于表格数据的 LIME 不同。数据的变化产生不同：从原始文本开始，通过从原始文本中随机删除单词来创建新文本。数据集用每个单词的二进制特征表示。

如果包含相应的单词，则特征为 1，如果已删除，则为 0。

9.2.2.1 示例

在此示例中，我们将YouTube 评论归类为垃圾评论或正常评论。

黑盒模型是在文档词矩阵上训练的深度决策树。每个评论是一个文档（= 一行），每一列是给定单词的出现次数。短决策树很容易理解，但在这种情况下，决策树非常深。也可以用循环神经网络或支持向量机来代替这棵树，用词嵌入（抽象向量）训练。让我们看一下这个数据集的两条评论和对应的类（1代表垃圾评论，0代表普通评论）：

	内容	班级
267	PSY是个好人	0
173	想找圣诞歌曲请访问我的频道	1

下一步是创建本地模型中使用的数据集的一些变体。例如，其中一条评论的一些变体：

For	Christmas	Song	visit	my	channel!	😉	prob	weight
1	0	1	1	0	0	1	0.17	0.57
0	1	1	1	1	0	1	0.17	0.71
1	0	0	1	1	1	1	0.99	0.71
1	0	1	1	1	1	1	0.99	0.86
0	1	1	1	0	0	1	0.17	0.57

每列对应句子中的一个单词。每行都是一个变体，1 表示该词是该变体的一部分，0 表示该词已被删除。其中一种变体的对应句子是“ Christmas Song visit my 😉”。“prob” 列显示每个句子变体的垃圾邮件预测概率。“权重”列显示变体与原始句子的接近度，计算为 1 减去被移除的单词的比例，例如，如果移除 7 个单词中的 1 个，则接近度为 1 - 1/7 = 0.86。

以下是 LIME 算法找到的两个句子（一个垃圾邮件，一个无垃圾邮件）及其估计的局部权重：

case	label_prob	feature	feature_weight
1	0.1701170	good	0.000000
1	0.1701170	a	0.000000
1	0.1701170	is	0.000000
2	0.9939024	channel!	6.180747
2	0.9939024	For	0.000000
2	0.9939024	😉	0.000000

“channel” 一词表示垃圾邮件的可能性很高。对于非垃圾评论，没有估计非零权重，因为无论删除哪个词，预测的类别都保持不变。

9.2.3 图像的 LIME

本节由 Verena Haunschmid 撰写。

用于图像的 LIME 与用于表格数据和文本的 LIME 的工作方式不同。直观地说，扰乱单个像素没有多大意义，因为不止一个像素对一类有贡献。随机改变单个像素可能不会对预测产生太大影响。因此，图像的变化是通过将图像分割成“超像素”并关闭或打开超像素来创建的。超像素是具有相似颜色的互连像素，可以通过将每个像素替换为用户定义的颜色（例如灰色）来关闭。用户还可以指定在每个排列中关闭超像素的概率。

9.2.3.1 示例

在此示例中，我们查看由 Inception V3 神经网络进行的分类。使用的图像显示了我烤的一些放在碗里的面包。由于每个图像可以有多个预测标签（按概率排序），我们可以解释顶部标签。预测最高的是“Bagel”，概率为 77%，其次是“Strawberry”，概率为 4%。下图显示了“Bagel”和“Strawberry”的 LIME 解释。解释可以直接显示在图像样本上。绿色表示这部分图像增加了标签的概率，红色表示减少。

图 9.8：左：一碗面包的图像。中间和右侧：由 Google 的 Inception V3 神经网络进行的图像分类前 2 类（百吉饼、草莓）的 LIME 解释。

“百吉饼”的预测和解释非常合理，即使预测是错误的——这些显然不是百吉饼，因为中间的洞不见了。

9.2.4 优点

即使你替换了底层的机器学习模型，你仍然可以使用相同的本地、可解释的模型进行解释。假设查看解释的人最了解决策树。因为你使用本地代理模型，所以你使用决策树作为解释，而实际上不必使用决策树来进行预测。例如，你可以使用 SVM。如果事实证明 xgboost 模型效果更好，你可以替换 SVM 并仍然使用决策树来解释预测。

本地代理模型受益于训练和解释可解释模型的文献和经验。

当使用 Lasso 或短树时，得到的解释很短（选择性）并且可能是对比性的。因此，他们做出人性化的解释。这就是为什么我在解释的接受者是外行或时间很少的人的应用程序中更多地看到 LIME。对于完整的归因来说，这还不够，所以我在合规场景中看不到 LIME，在这些场景中，法律可能要求你全面解释预测。同样对于调试机器学习模型，拥有所有原因而不是少数原因很有用。

LIME 是少数适用于表格数据、文本和图像的方法之一。

保真度度量（可解释模型与黑盒预测的近似程度）让我们很好地了解了可解释模型在解释感兴趣的数据实例附近的黑盒预测时的可靠性。

LIME 在 Python lime库 和 R（lime package和iml package）中实现，非常易于使用。

使用本地代理模型创建的解释可以使用原始模型训练之外的其他（可解释的）特征。当然，这些可解释的特征必须来自数据实例。

文本分类器可以依赖抽象词嵌入作为特征，但解释可以基于句子中词的存在或不存在。回归模型可以依赖于某些属性的不可解释的转换，但可以使用原始属性创建解释。

例如，回归模型可以针对调查答案的主成分分析 (PCA) 的组成部分进行训练，但 LIME 可以针对原始调查问题进行训练。与其他方法相比，使用 LIME 的可解释特征可能是一个很大的优势，尤其是当模型使用不可解释的特征进行训练时。

9.2.5 缺点

将 LIME 与表格数据一起使用时，邻域的正确定义是一个非常大的未解决问题。在我看来，这是 LIME 的最大问题，也是我建议谨慎使用 LIME 的原因。对于每个应用程序，你必须尝试不同的内核设置，并亲自查看解释是否有意义。不幸的是，这是我能给出的找到好的内核宽度的最佳建议。

在当前的 LIME 实现中可以改进采样。数据点是从高斯分布中采样的，忽略了特征之间的相关性。这可能导致不太可能的数据点，然后可用于学习局部解释模型。

解释模型的复杂度必须提前定义。这只是一个小小的抱怨，因为最终用户总是必须定义保真度和稀疏度之间的折衷。

另一个真正的大问题是解释的不稳定性。在文章³中，作者表明，在模拟环境中，对两个非常接近的点的解释差异很大。另外，根据我的经验，如果你重复采样过程，那么出来的解释可能会有所不同。不稳定意味着很难相信解释，你应该非常挑剔。

LIME 解释可以被数据科学家操