10. 回归损失最小化

Posted 2023-01-06 starrow

2.2 损失最小化

要评价监督学习的表现，自然的想法是使用模型预测的输出与真实的输出之间的误差（Error）[[1]]，不过原始的误差不能直接用于计算：对于回归，误差和输出值同样是实数，既可能是正数，也可能是负数，累加时会相互抵消，不能计算多个实例的误差之和；对于分类，输出的实际值和预测值都是定性的，误差因而是描述性的，无法计算其大小。所以，需要用另一个定量的标准来反映误差的大小。我们将该标准称为损失（Loss），根据输出的实际值和预测值来定义损失的函数称为损失函数L(y, f(x))[[2]]。损失越小，预测函数越准。损失函数度量的是预测函数在单个实例上的准确度，为了度量预测函数在任意实例上的准确度，我们采用损失函数的期望值（Expected loss）。下面就通过最小化损失期望值，分别确定回归和分类预测函数的行为。

2.2.1 回归损失最小化

对回归来说，损失函数应该避免正负误差相互抵消，并且具有对称性，即符号相反的两个误差具有同样的损失值。误差的绝对值函数符合这两点要求，但是该函数在零点处是不可导的，不便于后续分析。所以通常采用满足上述要求的最简单的可导函数——误差的平方（二乘）：

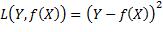
X和Y是遵循联合概率分布pX, Y(x, y)的随机变量，对预测函数的评价指标是损失函数在该分布上的期望值：

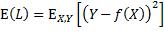
为了找到最小化该期望值的预测函数，把该期望值表达为，先对损失函数求关于X的条件期望，再对所得关于X的函数求期望：

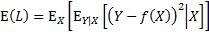
注意上式中内层的期望算子是应用于一个关于Y的函数，外层的期望算子则是应用于一个关于X的函数。为更易理解，可以用概率密度函数的形式来表达：

               
                  

   

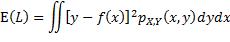
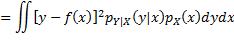
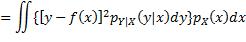
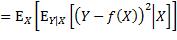
此双重积分的内层是关于y的积分，x被视为常数，积分的结果是一个关于x的函数，再通过外层积分求该函数的期望值。至此对f未做任何限制，即f可能是令E(L)取最小值的任何函数。从函数的定义出发，要确定f，就是要确定当x取任意值时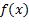 的值。根据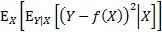 ，假设X取特定值x时，某个实数C使内层期望取最小值，那么 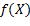就应该等于C。因此，f的定义可以表达为：

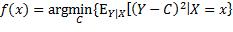
由概率论可知，当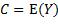 时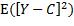， 取到最小值。所以f等于X取某x值时Y的条件期望值：

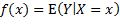
在对回归的具体问题没有任何知识和预测函数未做任何假定的情况下，得出了预测函数的以上表达式。我们惊喜地发现，它与叠加模型的假定是一致的，所以也可以用回归的平方误差损失最小化来说明叠加模型的合理性。

---

[[1]] 有些文献在回归场合使用另一个更专门的术语——残差（Residual），误差则在回归和分类的场合都适用，所以本书一律用误差。

[[2]] 当输入和输出取具体值x和y时，损失函数写作L(y, f(x))；当输入和输出被视为随机变量，如要计算期望值时，损失函数也成为随机变量，写作L(Y, f(X))。其他涉及到输入和输出的函数也做类似处理。