大数据因果推理与学习入门综合概述

Posted 2022-12-21 肖永威

在《原因与结果经济学》的开篇，给读者回答以下几个问题。

• 定期接受代谢综合征体检就能长寿吗？
• 看电视会导致孩子学习能力下降吗？
• 上录取分数高的大学收入就会更高吗？想必很多人的回答都是肯定的。

不过，经济学的权威研究已经推翻了上述全部说法。

1. 理解“因果推理”，便可摆脱传统观念的束缚

两个事件之间是否真的存在因果关系？为解答这一问题，近年来经济学研究倾注了巨大的心血。我们把正确区分因果关系和相关关系的方法论称为“因果推理”。

“因果”，顾名思义，即“原因与结果”。“推理”则指“根据某个事件推导其他事件，即经过推测和推断得出结论的过程”。换句话说，就是分析并判断两个事件是否分别为原因和结果的过程。

1.1. 因果关系与相关关系的概念

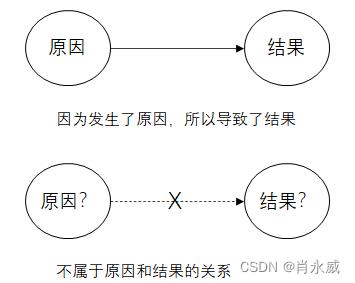
因果关系：如过两个事件中，前一个事件是后一个事件的原因，后一个事件是前一个事件的结果，则两个事件之间存在因果关系。

相关关系：如过一个事件变化后，另一个事件也随之变化，但二者不属于原因和结果的关系，则称他们之间存在相关关系。

存在相关关系的两个事件之间虽然有关联，但不属于因果关系。

1.2. 判断因果的三个要点

（1）是否“纯属巧合”？

（2）是否存在“第三变量”？术语说就是“混杂因素”。

（3）是否存在“逆向因果关系”？

如过两个变量之间存在因果关系，当原因再次出现时，相同的结果也会出现，而不是“纯属巧合”、“混杂因素（第三变量）”或“逆向因果关系”。另一方面，如过两个变量的关系只是相关关系，那么就会存在“纯属巧合”、“混杂因素”或“逆向因果关系”中的某一种情况。在相关关系的情况下，即使原因再次发生，也几乎不会得到相同的结果。

1.3. 证明因果关系需要“反事实”

没有时光机、也没有平行宇宙，就制造不出反事实吗？

克服“因果推理中的根本问题”，制造反事实，才正是以因果推理为基础的各种方法的根本所在。

例如：假设你想了解广告能为销售额带来多大的因果效应。广告的因果效应等于投放广告后的事实销售额和相同情况下没有投放广告的反事实销售额的差。主要方法有：

• 随机对照实验
• 自然实验与准实验
• 回归分析

1.4. 因果性和相关性的区别

举个例子：如果我们发现，夏天的时候，一个冰淇淋店的电费上涨的同时冰淇淋卖的也很好，我们可以说他们互相之间有因果的关系吗？不见得，他们之间可能只是统计上的相关性，而真正给他们带来的因果性的因子叫做气温，是因为气温的上升，导致电费的增加，也是因为气温的上升，导致了冰淇淋销量的上升。这个例子很好的向我们阐述了因果性和统计相关性的区别。

2. 因果革命：改变数据科学的新革命

随着机器学习建模越来越多的应用，企业对人工智能的要求也在进一步提高。近几年提及的「数智化」核心是智能决策，以数据驱动的方式实现自动化决策来提高整体运营效率。用户的需求的重心从预测性分析向指导性分析升级转移，预测性分析是告诉企业未来可能会发生什么，指导性分析也叫处方性分析，是告诉企业我们如果想要实现一个目标需要如何做，这是典型的智能决策问题。

机器学习主要用在预测性分析上，基本上没有能力解决指导性分析这样的决策问题，因此，因果学习正被学界和业界逐渐重视起来，其可以补充机器学习的一些短板，也满足了智能决策这类问题的需求。因果推断的重要性逐渐显示，被认为是人工智能领域的一次范式革命。

图灵奖得主、贝叶斯网络奠基人Judea Pearl说：”因果革命“是一场正在改变数据科学的新革命 — 。因果革命和以数据为中心的第一次数据科学革命，也就是大数据革命（涉及机器学习，深度学习机器应用，例如Alpha-Go、语音识别、机器翻译、自动驾驶等等 ）的不同之处在于，它以科学为中心，涉及从数据到政策、可解释性、机制的泛化，再到一些社会科学中的基础概念信用、责备和公平性， 甚至哲学中的创造性和自由意志 。可以说， 因果革命彻底改变了科学家处理因果问题的方式。

例如，“锻炼身体是否能够有利于健康？”见下图，x轴表示运动时间，y轴表示胆固醇水平。

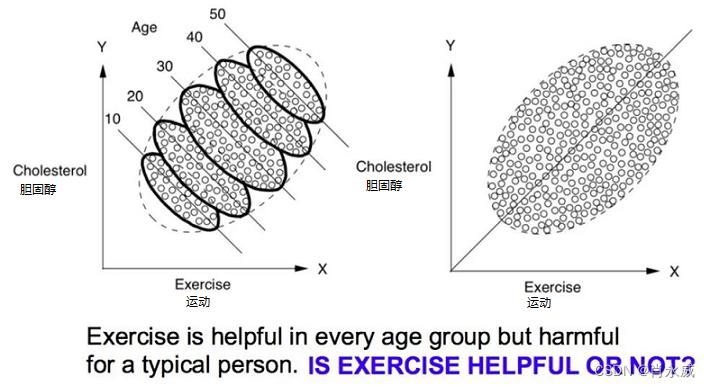
在上图（左）中，可以看大每个年龄组中都出现了向下的趋势，表明运动可能的确有降低人体胆固醇水平的效果；另一方面，在上图（右）中，同样的散点图并不依据年龄对数据进行分层，那么我们就会看到一个明显向上的趋势，这表明运动得越多，人体胆固醇水平就越高，这种矛盾在统计学中被成为辛普森悖论。

这个例子说明了数据可能对你讲出两个不同的故事。如果信息发生了一些变化，得到的结论就可能是不一样的。更加准确地来说，这个例子本质上是要回答因果问题，仅有数据信息而没有先验因果关系信息的时候，就可能得出与关注研究的问题相互矛盾的答案。回答因果问题需要因果信息。

Pearl 描述了一个因果推理的三级结构，把因果信息按其能够回答的类型进行分类。

第一层是关联（Association），它涉及由数据定义的统计相关性。大多数机器学习系统围绕这一层运行。

第二层是干预（Intervention），不仅涉及到能看到什么，还涉及一个干预或行动将会导致什么结果。作为例子，Pearl 提了一个问题：“如果我们把价格翻倍，将会发生什么？”

第三层是反事实（Counterfactual），是对以前发生的事情的反思和溯因，解决的是“如果过去作出不一样的行为，现在的结果会有何不同？”的问题。

因果革命中，数据科学的任务被重新分成了三类：预测、描述和反事实预测。

3. 因果推断入门

3.1. 因果推断研究的两个问题——从辛普森悖论讲起

• 第一个情况，对于心脏病，男女分别来看。

性别	未服药发病	未服药未发病	未服药发病率	服药发病	服药未发病	服药发病率
女性	1	19	5%	3	37	7.5%
男性	12	28	30%	8	12	40%
总体	13	47	21.6%	11	49	18.3%

这个药对人类有效，发生了什么？

• 第二个情况，分血压来看。

性别	未服药发病	未服药未发病	未服药发病率	服药发病	服药未发病	服药发病率
血压降低	1	19	5%	3	37	7.5%
血压升高	12	28	30%	8	12	40%
总体	13	47	21.6%	11	49	18.3%

这个药对人类有效，发生了什么？

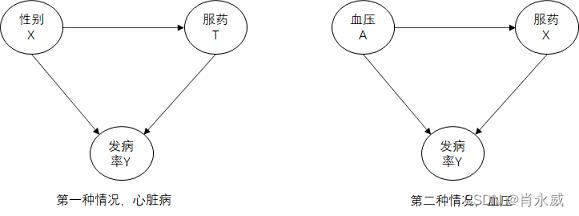
在第一个情况下，不同的性别有不同的服药意愿，也就是性别是服药和发病的共同原因，所以应该分层进行统计

在第二个情况下，服药会导致血压变化，也就是血压是服药和发病的共同结果，如果分层统计，则会低估服药的影响，总体的结论才是正确的。

从这两个辛普森悖论的例子我们可以看出现在因果推断最重要的两个研究方向：

• causal discovery：因果发现，也就是发现以上统计变量之间的因果关系，从统计变量中探寻出一个如上的因果图；
• causal effect：因果效应，在得到因果关系之后，确定效果，比如上面的问题是，知道因果图之后，确定服药之后发病率增加（减少）多少。

3.2. 常用评估指标与基本概念

3.2.1. 常用评估指标与变量定义

以第一种情况，“女性”心脏病患者服用心脏病药物为例来说明：

效果	W=0（未服药）	W=1（服药/干预）
未发病Y(=1)	19	37
发病Y(=0)	1	3

$Y_1(W=0)=19$
$Y_1(W=1)=37$
$Y_0(W=0)=1$
$Y_0(W=1)=3$

• Unit —— 单元，原子研究对象
• Treatment —— 干预/治疗，施加给一个原子对象unit的行为。在二元Treatment的情况下(即W=0 或 1 )，Treatment组包含接受Treatment为 W=1 的unit，而对照组包含接受Treatment为 W=0 的unit。

例如，第一种情况服药T，干预可以是一项政策、一项措施或者一项活动等。

• Outcome —— 结果，在对unit进行Treatment或者仅仅作为对照之后unit随后产生的反应/结果，一般用 Y 表示

例如，第一种情况发病率Y。

• Treatment Effect —— 因果效应，对unit进行不同Treatment之后unit产生的Outcome的变化，这种效应可以定义在整体层面、treatment组层面、子组层面和个体层面

• 整体层面 —— Average Treatment Effect(ATE)，平均干预效果
  $ATE=E[Y(W=1)-Y(W=0)]$

$ATE=(Y_1(W=1)-Y_1(W=0))/(Y_1(W=1)+Y_1(W=0))=(37-19)/36=50\%$

• Treatment组层面 —— Average Treatment Effect on the Treated Group (ATT)，Treatment组中的平均干预效果
  $ATT=E[Y(W=1)\mid W=1]-E[Y(W=0)\mid W=1]$

$ATE=(Y_1(W=1)-Y_0(W=1))/(Y_1(W=1)+Y_0(W=1))=(37-3)/40=85\%$
服药干预组中，平均干预效果为85%。

• 子组层面 —— Conditional Average Treatment Effect (CATE)
  $CATE=E[Y(W=1)\mid X=x]-E[Y(W=0)\mid X=x]$

• 个体层面 —— Individual Treatment Effect (ITE)
  $IT{E}_i=E[Y_i(W=1)-Y_i(W=0)]$

• Potential Outcome —— 潜在结果，对于每对unit-treatment，当对unit施加相应的treatment之后产生的结果

潜在结果
一个或多个处理作用（干预T）在个体上产生的预期效果我们称之为潜在结果 (Potential outcome)。之所以称为潜在结果是因为在一个个体上最终只有一个结果会出现并被观察到，也就是和个体所接受的处理相对应的那个结果。另外的潜在结果是观察不到的，因为它们所对应的处理并没有实际作用在该个体上。

• Observed Outcome —— 观测结果，已经发生的事实，对unit施加某个treatment之后产生的能观测到的结果

• Counterfactual Outcome —— 反事实结果， 已经发生事实的其他对立面，也即对某个unit未采用的其他treatment带来的潜在结果。

• 不可见的反事实空间（Counterfactual）
  对于特定个体的特定状态，我们只能对其进行一次操作（比如用药）然后观察效果，而无法获知进行相对应操作（比如服用安慰剂或不用药）下的效果。而这种无法获知的状态就称为“Counterfactual”。如果我们能够既知道real world又知道counterfactual world的情况，那么二者做差即可得到causal effect。但很遗憾counterfactual永远不可知。

• 混淆变量（Confounding Factor OR Covariates）
  Treatment变量T和effect变量Y可能会同时受到某一第三方变量X的影响，导致观察到的T对Y的影响其实并不一定是真实的作用关系。比如要研究某种药对病人的效果，但研究过程中忽略了年龄的因素，结果治疗组和对照组治疗效果上的差别实际是病人年龄差异导致的，这种情况下年龄就称为混淆变量。

• Conditional Independent Assumption(CIA) 条件独立假设问题
  这里的独立是概率论意义下的独立，即A、B独立，则$P(AB)=P(A)P(B)$，不独立情况下是$P(AB)=P(A|B)P(B)$。

3.2.2. 因果模型概述

鲁宾因果模型 Rubin Causal Model（RCM）

鲁宾因果模型 Rubin Causal Model (RCM) ，也称为 Neyman-Rubin 因果模型，是一种基于潜在结果框架的因果统计分析方法，框架有三个基本构成要件：潜在结果、稳定性假设和分配机制。

鲁宾因果模型是基于潜在结果的想法。例如，如果一个人上过大学，他在 40 岁时会有特定的收入，而如果他没有上过大学，他在 40 岁时会有不同的收入。为了衡量这个人上大学的因果效应，我们需要比较同一个人在两种不同的未来中的结果。由于不可能同时看到两种潜在结果，因此总是缺少其中一种潜在结果。这种困境就是“因果推理的基本问题”。

由于因果推理的根本问题，无法直接观察到单元级别的因果效应。然而，随机实验允许估计人口水平的因果效应。随机实验将人们随机分配到对照组：大学或非大学。由于这种随机分配，各组（平均）相等，40 岁时的收入差异可归因于大学分配，因为这是各组之间的唯一差异。然后可以通过计算处理（上大学）和对照（非上大学）样本之间的平均值差异来获得平均因果效应（也称为平均处理效应）的估计值。

潜在结果框架的第三个要件是分配机制。分配机制是描述为什么有的人在干预组，有的人在控制组，或者分配机制是描述哪个潜在结果可以被观测到的机制。因果推断中分配机制非常重要，对分配机制的了解有助于进行正确的因果推断。

结构因果模型 Structural Causal Model（SCM）

结构因果模型（SCM）结合了图形建模、结构方程、反事实和介入逻辑。

结构因果模型（SCM）是由内生变量$V$、外生变量$U$和映射函数$F$构成。因果的定义：若$Y$在$f_X$ 的定义域中，则$Y$是$X$的直接原因 ；如果$Y$是$X$的直接原因，或者是直接原因的原因，则$Y$是$X$的原因。

$U$中的变量称为外生变量，它们属于模型的外部，不必解释它们变化的原因。$V$中的变量称为内生变量，模型中每一个内生变量都至少是一个外生变量的后代。外生变量没有祖先节点，不是内生变量的后代。

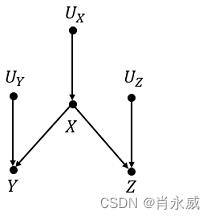
V = X , Y , Z , U = U X , U Y