GRU回归预测基于matlab粒子群算法优化门控循环单元PSO-GRU神经网络回归预测（多输入单输出）含Matlab源码 2286期

Posted 2022-12-19 海神之光

⛄一、CNN-GRU数据预测

1 理论基础
1.1 CNN算法
负荷序列数据为一维数据，用一维卷积核对数据进行卷积处理，以获取数据的特征。
现设定卷积核的维度为3，移动步长为1，对输入数据进行卷积，以获得特征图图谱，即：

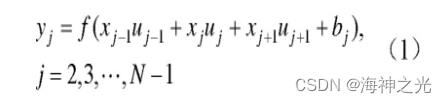
式中：yj为第j个位置的特征值输出；xj为第j个位置的数据值；uj为第j个位置的卷积核值。

1.2 GRU算法
将经过卷积之后产生的特征序列作为GRU的输入。GRU由LSTM发展而来，LSTM是RNN的变体。RNN网络通过对输入信号的循环保证了信号的持续存在。LSTM是由RNN网络改进而来，在RNN的基础上加入了记忆单元和门机制，有效地解决了长序列训练中存在的梯度消失和梯度爆炸问题。

LSTM用输入门、遗忘门和输出门3个门函数来控制输入值、遗忘值和输出值。GRU网络较LSTM网络有所简化，GRU网络由新门和重置门两个门函数构成，其结构如图1所示。

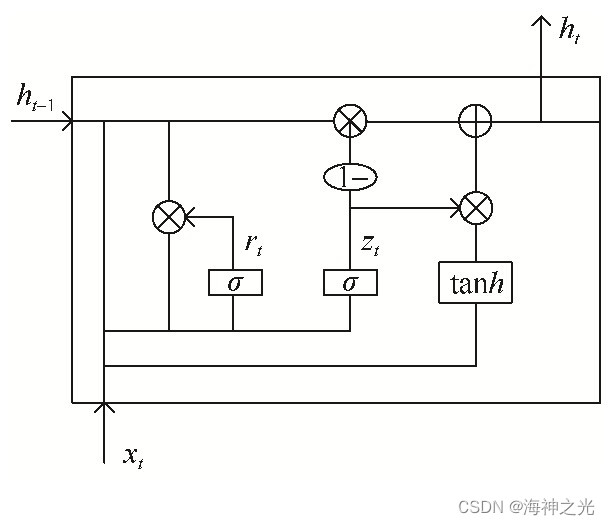
图1 GRU的网络结构图
zt为更新门，用来决定上一层隐藏层状态中有多少信息传递到当前的隐藏状态ht中，经过sigmoid函数将结果映射到0～1之间，即：

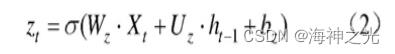
rt为重置门，决定上一时刻隐藏层状态有多少信息需要被遗忘，经过sigmoid函数将结果映射到0～1之间，越接近1信息越容易被保留，即：

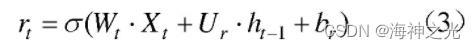
确定当前的记忆内容，将重置门rt与ht–1进行Hadamard乘积决定当前的记忆内容中要遗忘多少上一时刻的隐藏层的内容，然后与新的输入数据结合放入tanh激活函数中，即：

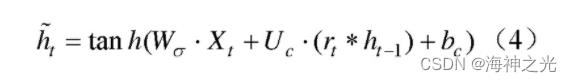
最后确定当前隐藏层保留的信息，通过zt和1–zt确定哪些历史数据和当前数据需要更新，即：

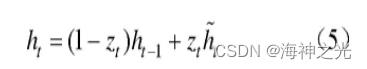
2 PSO原理
粒子群算法（PSO）是一种群体智能优化算法。该算法最早由Kennedy和Eberhart在1995年提出的。该算法最早来源于对鸟类搜寻食物行为的研究[10]。算法中粒子的速度和位置会发生相应的变化，在每一次迭代过程中，粒子根据自身适应度值调整下次飞行的方向和速度。粒子是有记忆的，每一次迭代都会更新种群的最优解，速度和位置更新公式如式（10）和（11):

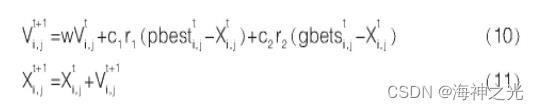
⛄二、部分源代码

%% 清空环境变量
warning off % 关闭报警信息
clear all % 清空变量
clc % 清空命令行
% close all % 关闭开启的图窗

%% 导入数据
% 训练集——190个样本
P_train = xlsread(‘data1’,‘training set’,‘B2：G191’)‘; T_train= xlsread(‘data1’,‘training set’,‘H2：H191’)’;
% 测试集——44个样本
P_test=xlsread(‘data1’,‘test set’,‘B2:G45’)‘;T_test=xlsread(‘data1’,‘test set’,‘H2:H45’)’;
shuru_num = size(P_train ,1); % 输入维度
shuchu_num=1;
N = size(P_test, 2); % 测试集样本数
M = size(P_train, 2); % 训练集样本数

%% 数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax(‘apply’, P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax(‘apply’, T_test, ps_output);

%% 优化算法
pop = 20; %种群数量
Max_iter = 20; %最大迭代次数
lb = [10 0.001] ; %下边界
ub = [200 0.015]; %上边界
dim = 2; %维度
fobj=@(X)fobj(X,p_train,t_train,p_test,t_test,shuru_num,shuchu_num );
[ Best_score, Best_P,curve] = PSO(pop, Max_iter, lb, ub, dim, fobj);

%% 重新训练
disp([‘最佳光滑因子值为’,num2str(Best_P)])
Best_P(1)=round(Best_P(1));
layers = [ …
sequenceInputLayer(shuru_num)
gruLayer(Best_P(1))
fullyConnectedLayer(shuchu_num)
regressionLayer];
options = trainingOptions(‘adam’, … % 梯度下降
‘MaxEpochs’,50, … % 最大迭代次数
‘GradientThreshold’,1, … % 梯度阈值
‘InitialLearnRate’,Best_P(2));
net = trainNetwork(p_train,t_train,layers,options);
%% 预测
net = resetState(net);% 网络的更新状态可能对分类产生了负面影响。重置网络状态并再次预测序列。
% [~,t_sim1]= predictAndUpdateState(net,p_train);%% 采用最佳方法建立GRU网络
[~,t_sim1]= predictAndUpdateState(net,p_train); %训练集预测
[net,t_sim2]= predictAndUpdateState(net,p_test); %测试集预测

%% 数据反归一化
T_sim1 = mapminmax(‘reverse’, t_sim1, ps_output);
T_sim2 = mapminmax(‘reverse’, t_sim2, ps_output);

%% 均方根误差
error1 = sqrt(sum((T_sim1 - T_train).^2) ./ M);
error2 = sqrt(sum((T_sim2 - T_test ).^2) ./ N);

%% 适应度曲线
figure
plot(1 : length(curve), curve,‘r-’, ‘LineWidth’, 1.5);
title(‘PSO-GRU’, ‘FontSize’, 13);
xlabel(‘迭代次数’, ‘FontSize’, 10);
ylabel(‘适应度值’, ‘FontSize’, 10);
grid off

⛄三、运行结果

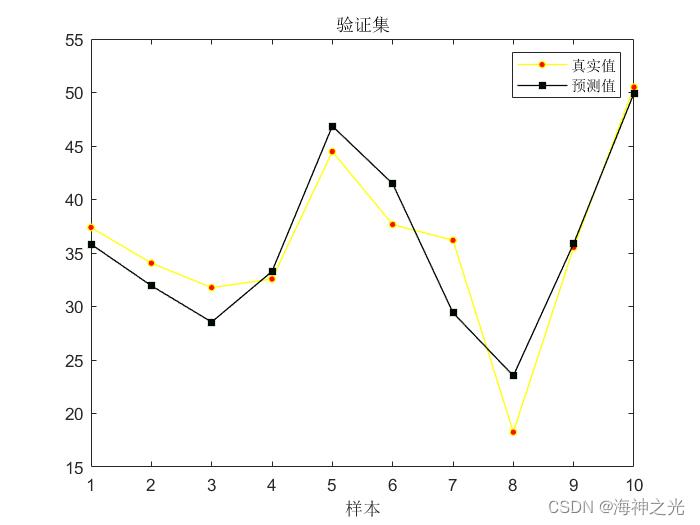
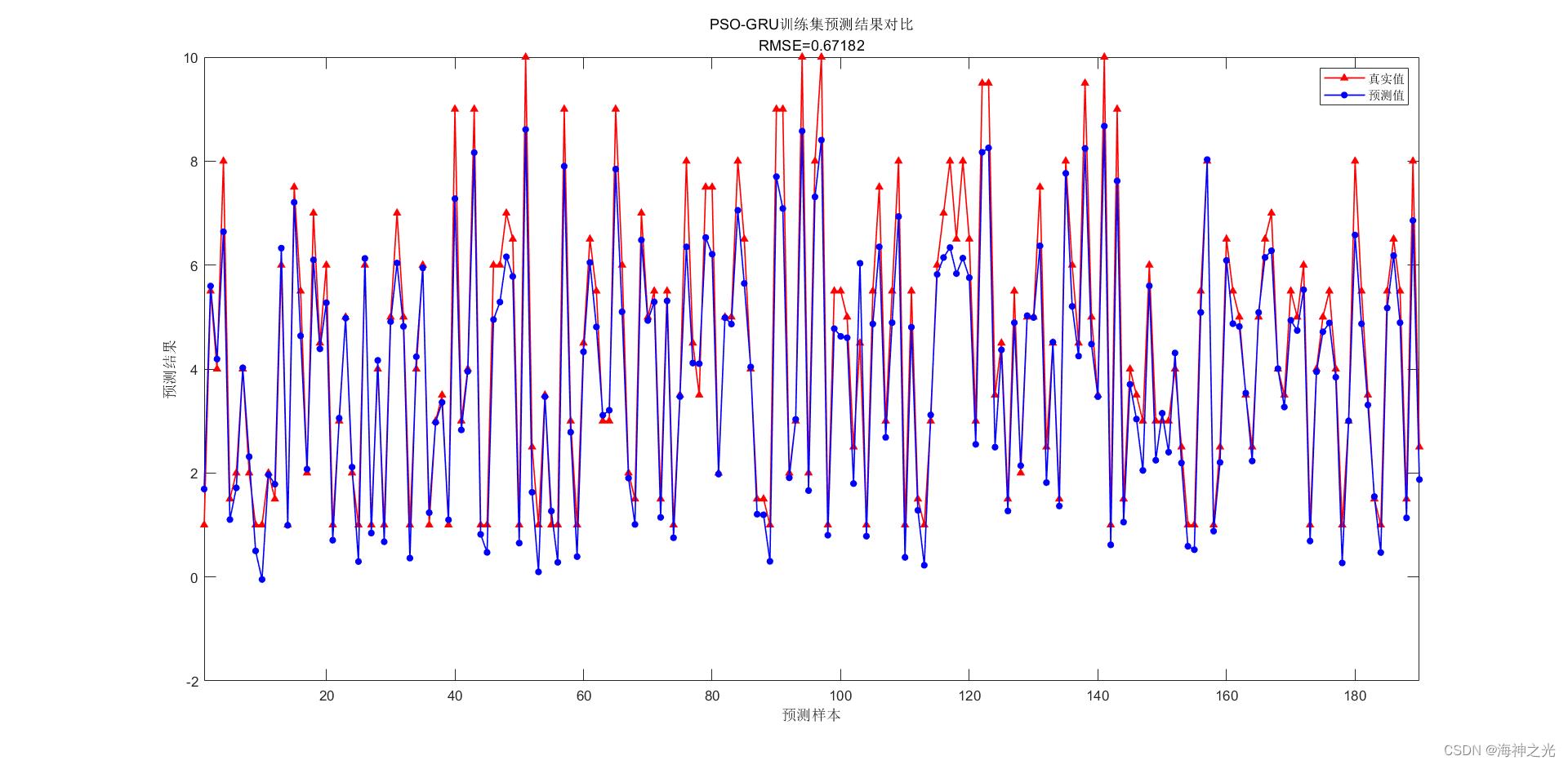
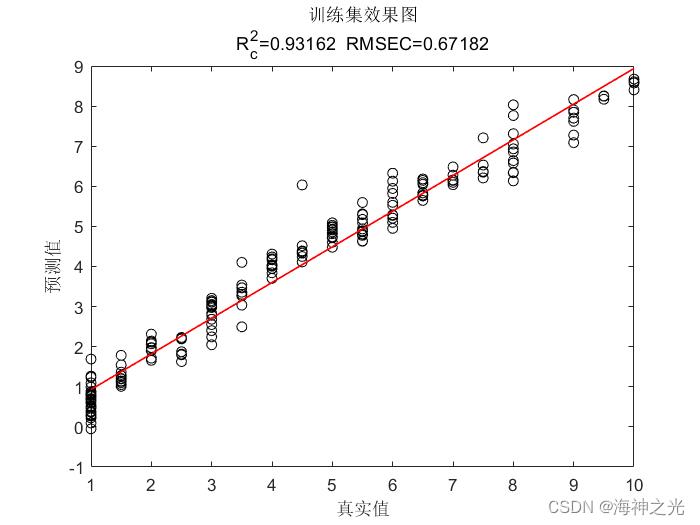
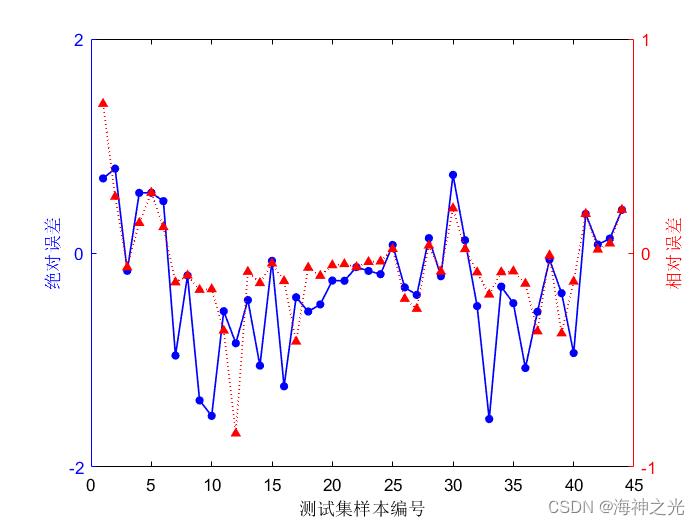
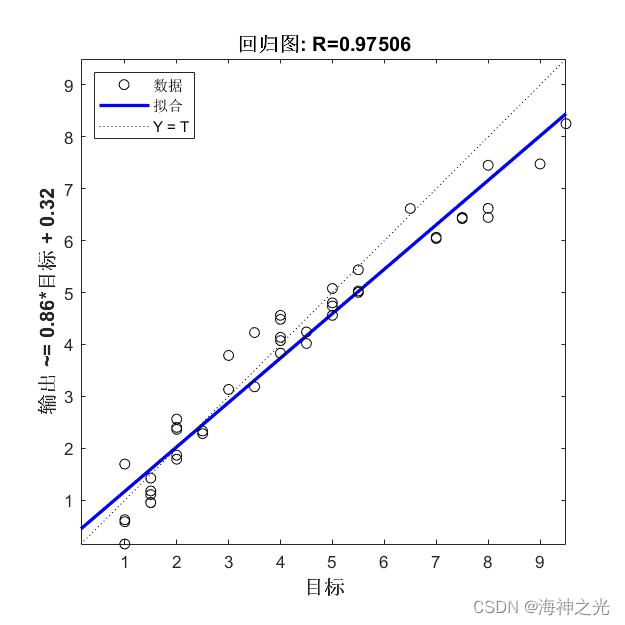
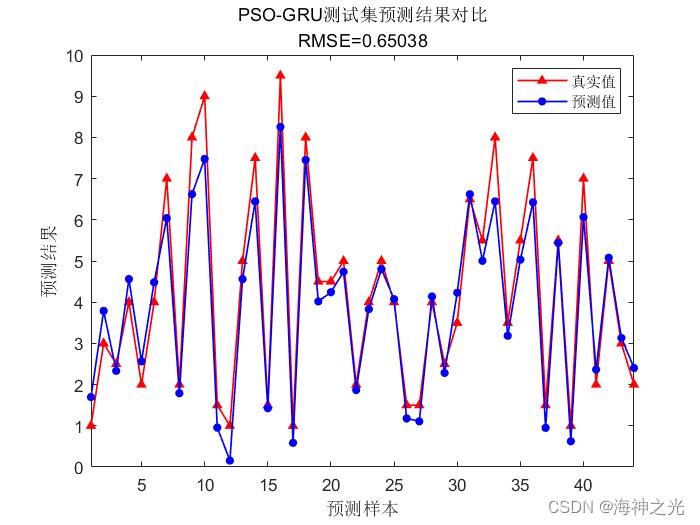
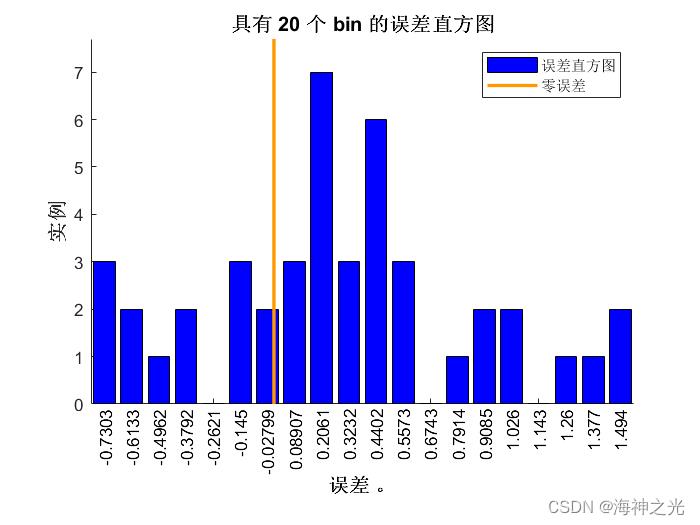
⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]王超,刘世明.基于PSO-GRU的光伏电站短期功率预测研究[J].工业控制计算机. 2021,34(10)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除