2021上海ICPC--H.Life is a Game--Kruskal重构树--铜牌拦路虎

Posted 2022-12-16 XINNNNNNNYU

差不多两个小时的时候过了4题，在铜尾，看了一下榜单，去掉打星还有30名左右可以掉，起初掉的很慢，自以为还是很有希望的，然后看着H题过得越来越多，但是三个没有丝毫思路，在封榜前掉出了奖牌区。最后开了J，交了274发随机，赛后看了下得分，有近10发已经过了80%了，还是被大数据卡掉了。归根结底，与铜牌失之交臂的罪魁祸首就是Kruskal重构树，学了一下还是很简单的，要是赛时翻一翻打印出来的oiwiki的图论说不定能翻到。

上上场ccpc威海因为被卡常了，差了两发罚时，也是铁首。以两个铁首结尾还是感到遗憾，寄希望于明年昆明了，寒假一定好好训练。

Kruskal重构树

简介

Kruskal 重构树是图的一种生成树，主要解决路径边权限制问题。Kruskal 重构树有按深度单调的性质，所以很容易就可以解决边权的取值限制。

算法流程

顾名思义，这个算法和求最小生成树的Kruskal非常类似。

1. 把所有边按照边权从小到大排序
2. 按顺序遍历每一条边（a,b,c），如果a，b已经在一个联通块内了，则跳过，否则我们构造一个新点x，由它来连接这两个点，然后x的点权就是c。并且将并查集的祖先设为x，即fa[a] = fa[b] = x;

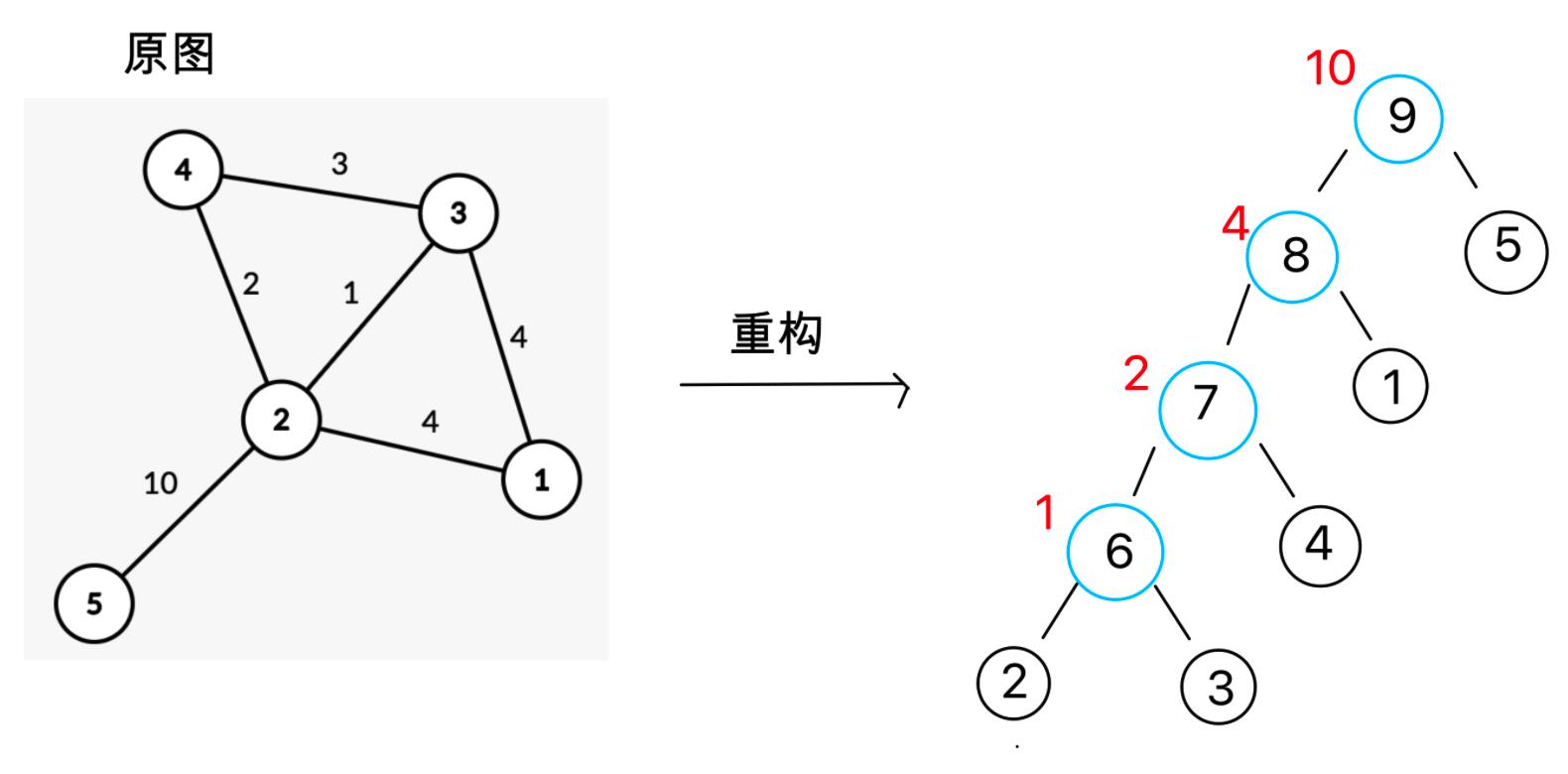
重构树的性质

1.重构树的节点个数是2*n-1，因为树的每条边成为一个新增节点。
2.原来的点都是叶子结点
3.这是一棵二叉树，最后增加的点是根节点
4.新增点的点权按加入顺序是非严格递增的
5.从一个点x（通常是原图的点，也就是新图里的叶子结点）出发经过的边边权<=w能到达的点就是从x出发找到第一个祖先节点ed，ed的点权>w，则该点的子树的叶子节点就是原来图中能到达的所有点。

---

Life is a Game

题意

给你一张图和所有点的点权，所有边的边权。然后有1e5次询问，每次给你一个起点st和一个金币数val，每走到一个点金币数可以加上点权，但是只有金币数大于等于边权才能走那条边，通过一条边不会消耗金币，问最后的金币数是多少。

思路

最后不能走的条件就是当前已走过的点的点权和加上初始的值小于周围可走边的权值，是一个边权限制的问题（有点强行解释），理所应当的我们想到Kruskal重构树（屁嘞，学都没学过）。

我们画出样例的重构树
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7JP1tEJe-1670481718886)(https://pic.baixiongz.com/uploads/2021/11/30/24a4f27006dcc.jpeg)]

根据题意我们知道停止移动的条件是新点的点权（原来的边权）减去经过的所有点的点权和（也就是他的子树所有点权和） > val。因为边权在递增，子树点权和也在递增，所以停止的点可能有很多个，且不是连续的，我们要找到最靠近起点的，也就是深度最深的。

• 我们可以对新增的点维护一个他子树所有点权和
• 然后用两个跳表，一个是pre来维护节点编号，一个v（表示边权减去子树所有点权和）来维护最大值，用来快速找到最接近起点的终止位置。

代码

#include<bits/stdc++.h>
using namespace std;

#define ios ios::sync_with_stdio(false);cin.tie(0);
#define mem(a,b) memset(a,b,sizeof a)
#define PII pair<int,int>
#define ll long long
#define ull unsigned long long
#define fi first
#define se second
#define endl '\\n'
#define PI acos(-1.0)
#define lcm(a,b) a/gcd(a,b)*b
#define INF 0x3f3f3f3f3f3f3f3f
#define debug(a) cerr<<#a<<"="<<a<<endl;
#define Adebug(a,i) cerr<<#a<<"["<<i<<"]="<<a[i]<<endl;
#define int long long
#define rep(i, a, b) for(int i = (a); i <= (b); i ++)
#define per(i, a, b) for(int i = (a); i >= (b); i --)
#define vi vector<int>
#define vpii vector<PII>
#define pb push_back
#define rvs(s) reverse(s.begin(),s.end())
#define all(s) s.begin(),s.end()
#define sz(s) (int)(s.size())
#define lb(s) ((s) & (-s))
#define mk(s, t) make_pair(s, t)
#define CN puts("NO")
#define CY puts("YES")



inline void wt(int x)cout << x;
inline void wtl(int x)cout << x << endl;
inline void wtb(int x)cout << x << ' ';
inline void wt(char x)cout << x;
inline void wtl(char x)cout << x << endl;
inline void wtb(char x)cout << x << ' ';
inline void wt(string x)cout << x;
inline void wtl(string x)cout << x << endl;
inline void wtb(string x)cout << x << ' ';
template <typename T> bool ckmax(T &x, T y)return x < y ? x = y, true : false;
template <typename T> bool ckmin(T &x, T y)return x > y ? x = y, true : false;
int qmi(int a, int k, int p)int res = 1;while (k)if (k & 1) res = (ll)res * a % p;a = (ll)a * a % p;k >>= 1;return res;
int qpow(int a,int b)int res = 1;while(b)if(b&1) res *= a;b>>=1;a*=a;return res;
int mo(int x,int p)return x = ((x%p)+p)%p;
int gcd(int a,int b)return b?gcd(b,a%b):a;
const int maxn = 1e6+7;
const int mod = 1e9+7;
int dx[] = 0,0,1,-1, dy[] = 1,-1,0,0;

int T = 1,N,M,K,Q;
int A[maxn],B[maxn];

struct Edge
	int a,b,c;
;
int cmp(Edge a, Edge b)
	return a.c < b.c;


int fa[maxn];
int find(int x)
	return fa[x] == x ? x : (fa[x]=find(fa[x]));


int v[maxn][20];

int pre[maxn][20];

void solve()
	cin >> N >> M >> Q;
	rep(i,1,2*N) fa[i] = i;//最后点的个数是2*N-1
	rep(i,1,N) cin >> A[i];
	vector<Edge> edge;
	while(M--)
	
		int u, v, w;
		cin >> u >> v >> w;
		edge.pb(u,v,w);
	

	sort(all(edge),cmp);

	int node = N + 1;//新增点开始编号
	for(auto e : edge)
		int a = e.a, b = e.b, c = e.c;
		int ra = find(a), rb = find(b);
		if(ra != rb)
			A[node] = A[ra] + A[rb];//子树的点权和，不包括自己
			pre[ra][0] = pre[rb][0] = node;//上面一个节点的编号 
			//处理跳表
			v[ra][0] = c - A[ra];
			v[rb][0] = c - A[rb];
			fa[ra] = fa[rb] = node++;//合并并查集
		
	
	//预处理
	per(i,node-1,1)
		rep(j,1,18)
			pre[i][j] = pre[pre[i][j-1]][j-1];
			v[i][j] = max(v[i][j-1],v[pre[i][j-1]][j-1]);
		
	


	rep(i,1,Q)
		int st,val;
		cin >> st >> val;
		per(j,18,0)
			if(pre[st][j]!=0 && v[st][j]<=val) st = pre[st][j];//等于0说明跳到2*N-1之外了（不存在的点）；最大值小于等于val说明st到pre[st][j]路径中间都是满足的，所以继续往根节点跳
		
		//最后st就是不能走的那个点
		cout << val + A[st] << endl;
	
	

	

signed main()

	IOS
	// cin >> T;
	while(T--) solve();
  return (0-0); //<3