寒假每日一题棋盘挑战（个人练习）详细题解+推导证明（第十六天）

Posted 2022-12-15 我是管小亮

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了寒假每日一题棋盘挑战（个人练习）详细题解+推导证明（第十六天）相关的知识，希望对你有一定的参考价值。

文章目录

前言
题目
详细题解
- - - 写法1
    - 推导证明
举一反三
总结

前言

今天是经典的深度优先搜索问题，即八皇后问题。

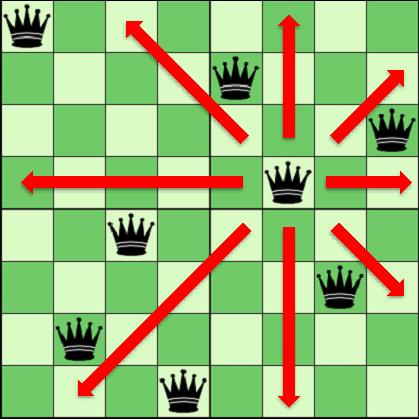
作为经典问题，我发现了一种新的写法，不需要开二维数组即可完成。

题目

给定一个 N×N 的棋盘，请你在上面放置 N 个棋子，要求满足：

每行每列都恰好有一个棋子
每条对角线上都最多只能有一个棋子

    1   2   3   4   5   6
  -------------------------
1 |   | O |   |   |   |   |
  -------------------------
2 |   |   |   | O |   |   |
  -------------------------
3 |   |   |   |   |   | O |
  -------------------------
4 | O |   |   |   |   |   |
  -------------------------
5 |   |   | O |   |   |   |
  -------------------------
6 |   |   |   |   | O |   |
  -------------------------

上图给出了当 N=6 时的一种解决方案，该方案可用序列 2 4 6 1 3 5 来描述，该序列按顺序给出了从第一行到第六行，每一行摆放的棋子所在的列的位置。

请你编写一个程序，给定一个 N×N 的棋盘以及 N 个棋子，请你找出所有满足上述条件的棋子放置方案。

输入格式

共一行，一个整数 N。

输出格式

共四行，前三行每行输出一个整数序列，用来描述一种可行放置方案，序列中的第 i 个数表示第 i 行的棋子应该摆放的列的位置。
这三行描述的方案应该是整数序列字典序排在第一、第二、第三的方案。
第四行输出一个整数，表示可行放置方案的总数。

数据范围

$6 \leq N \leq 13$

输入样例：
6
输出样例：
2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4

详细题解

写法1

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 15;

int n;
bool col[N], dg[N*2], udg[N*2];
int path[N], ans;

void dfs(int x)

    if(x > n)
    
        ++ ans;
        if (ans <= 3)
        
            for (int i = 1; i <= n; ++ i )
                cout << path[i] << " ";
            cout << endl;
        
        return ;
    
    
    for (int y = 1; y <= n; ++ y )
        if (!col[y] && !dg[x - y + n] && !udg[x + y])
        
            path[x] = y;
            col[y] = dg[x - y + n] = udg[x + y] = true;
            dfs(x + 1);
            
            path[x] = 0;
            col[y] = dg[x - y + n] = udg[x + y] = false;
        


int main()

    cin >> n;
    dfs(1);
    cout << ans << endl;
    
    return 0;