SLAM-Eigen库
Posted KAI-yq
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了SLAM-Eigen库相关的知识,希望对你有一定的参考价值。
目录
使用Eigen库的原因
开源线性代数库
矩阵运算,表达刚体旋转
三维空间中刚体的旋转表示
1.旋转矩阵
R和t组成齐次变换矩阵T,表达连续的欧式变换
R的逆矩阵表示相反的旋转
扩展:欧几里得坐标系(即欧式坐标)
定义了内积,角,距离。三维坐标系下的外积:
内积:

几何概念,角:


距离:
d(x,y)=||x-y||
三维坐标系下的外积:
齐次坐标下,向量a x b表示与a,b都垂直的向量
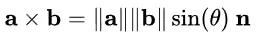
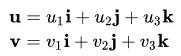

扩展:齐次坐标在欧式空间的好处
1.方便表达点在线上或平面上
直线 l 用ax + by + c = 0表示
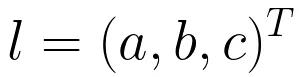
p的齐次坐标(x,y,1)
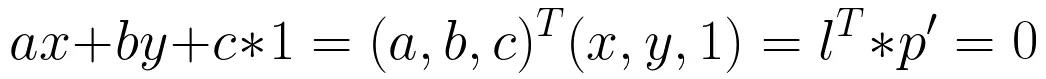
面的原理同上
2.方便表达直线和交点
在齐次坐标下,可以用两个点 p, q 的齐次坐标叉乘结果来表达一条直线 l,也就是
l = p x q
也可以使用两条直线 l, m 的叉乘表示他们的交点 x
x = l x m
 3.方便区分点和向量
3.方便区分点和向量
(1)从普通坐标转换成齐次坐标时,
如果(x,y,z)是个点,则变为(x,y,z,1);
另:如果是点(x,y,z,0)则表示无穷远处的点
如果(x,y,z)是个向量,则变为(x,y,z,0)
(2)从齐次坐标转换成普通坐标时 ,
如果是(x,y,z,1),则知道它是个点,变成(x,y,z);
如果是(x,y,z,0),则知道它是个向量,仍然变成(x,y,z)
4.更优美的表达欧式变换
将平移的加法变成矩阵相乘
当面对连续的旋转平移,就体现了优势,变成了连续的矩阵相乘
2.四元数
w+xi+yj+zk 即(w,x,y,z)
单位四元数才能描述旋转,使用前要归一化:q.normalize( )
Quaterniond (1, 0, 0, 0) Eigen里四元数赋值顺序是w,x,y,z,但实际内部存储顺序是x,y,z,w,输出格式也是x,y,z,w;
3.旋转向量
一个轴,一个角描述旋转,360度一圈,所以有奇异性
旋转向量到旋转矩阵有罗德里格斯公式,opencv和MATLAB有函数实现
旋转向量和旋转矩阵的转换对应于李代数和李群的映射
4.欧拉角
yaw,pitch,roll轴
俯仰角正负90度,一次和第三次旋转共轴,丢失一个自由度
三维旋转需要四个变量
Eigen库的安装与基础
安装:sudo apt-get install libeigen3-dev
1.Eigen库只有头文件,没有.so,.a等二进制库文件
在CMakeLists.txt里只需要添加头文件路径,不需要target_link_libraries将程序链接到库
#添加Eigen库
find_package(Eigen3)
#添加Eigen头文件
include_directories($EIGEN3_INCLUDE_DIR)
2.转换图
 3.基本语法
3.基本语法
Eigen库中的向量是特殊的矩阵,维度为1
Matrix3d H = Matrix3d::Zero(); //元素类型为double,大小为3*3
Vector3d b = Vector3d::Zero(); //默认为列向量
构造欧式变换矩阵:
Eigen::Isometry3d T = Eigen::Isometry3d::Identity();// 虽然称为3d,实际是4*4
T.matrix(): 1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
T.rotate ( rotation_vector );// 按照rotation_vector进行旋转
T.pretranslate ( Eigen::Vector3d ( 1,3,4 ) );// 把平移向量设成(1,3,4)
旋转矩阵转欧拉角
Eigen::Matrix3d rotation_matrix;
Eigen::Vector3d eulerAngle=rotation_matrix.eulerAngles(0,1,2);
以上是关于SLAM-Eigen库的主要内容,如果未能解决你的问题,请参考以下文章