李宏毅2017机器学习课程 回归

Posted 临风而眠

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了李宏毅2017机器学习课程 回归相关的知识，希望对你有一定的参考价值。

李宏毅2017机器学习课程 P3 回归 Regression

回归定义

  • 找到一个函数function，通过输入特征x，输出一个数值scalar

举例:Pokemon精灵攻击力预测(Combat Power of a Pokemon)

李宏毅老师真是太有趣了哈哈哈哈

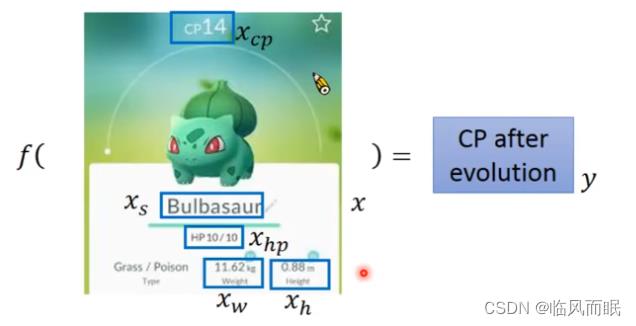
  • 输入：进化前的CP值、物种（Bulbasaur)、血量（HP）、重量（Weight）、高度（Height）

  • 输出：进化后的CP值

模型步骤

  1. 模型假设，选择模型框架（线性模型）
  2. 模型评估，如何判断众多模型的好坏（损失函数）
  3. 模型优化，如何筛选最优的模型（梯度下降）

Step1：模型假设-线性模型

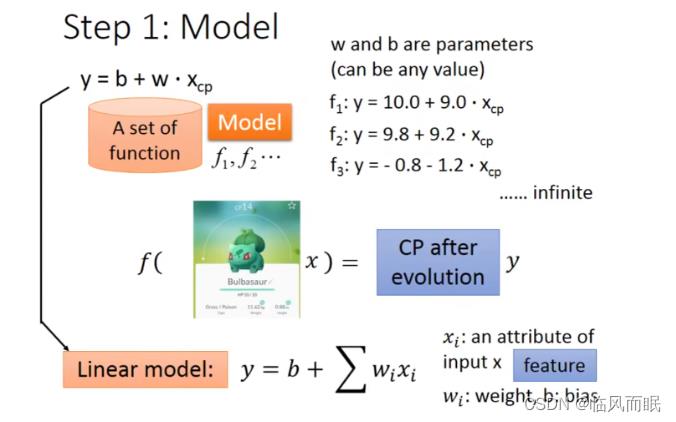
一元线性模型（单个特征）

  • 以一个特征 x c p x_cp xcp​为例，线性模型假设 y = b + w ⋅ x c p y = b + w·x_cp y=b+w⋅xcp​ ，所以 ω \\omega ω 和 b b b 可以猜测很多模型，比如

    f 1 : y = 10.0 + 9.0 ⋅ x c p f 2 : y = 9.8 + 9.2 ⋅ x c p f 3 : y = − 0.8 − 1.2 ⋅ x c p   ⋅ ⋅ ⋅ f_1: y = 10.0 + 9.0·x_cp \\\\ f_2: y = 9.8 + 9.2·x_cp \\\\ f_3: y = - 0.8 - 1.2·x_cp \\ ··· f1​:y=10.0+9.0⋅xcp​f2​:y=9.8+9.2⋅xcp​f3​:y=−0.8−1.2⋅xcp​ ⋅⋅⋅

  • 虽然可以做出很多假设，但在这个例子中，显然 f 3 : y = − 0.8 − 1.2 ⋅ x c p f_3: y = - 0.8 - 1.2·x_cp f3​:y=−0.8−1.2⋅xcp​ 的假设是不合理的，不能进化后CP值是个负值吧~~

多元线性模型（多个特征）

  • 在实际应用中，输入特征肯定不止 x c p x_cp xcp​ 这一个。例如，进化前的CP值、物种（Bulbasaur）、血量（HP）、重量（Weight）、高度（Height）等，特征会有很多

    • 所以我们假设 线性模型 Linear model： y = b + ∑ w i x i y = b + \\sum w_ix_i y=b+∑wi​xi​

    • x i x_i xi​：就是各种特征(fetrure) x c p , x h p , x w , x h , ⋅ ⋅ ⋅ x_cp,x_hp,x_w,x_h,··· xcp​,xhp​,xw​,xh​,⋅⋅⋅

    • ω i \\omega_i ωi​：各个特征的权重 ω c p , ω h p , ω w , ω h , ⋅ ⋅ ⋅ \\omega_cp,\\omega_hp,\\omega_w,\\omega_h,··· ωcp​,ωhp​,ωw​,ωh​,⋅⋅⋅

    • b b b：偏移量

注意：接下来的内容需要看清楚是【单个特征】还是【多个特征】的示例

Step2：模型评估-损失函数

【单个特征】: $x_cp $

收集和查看训练数据

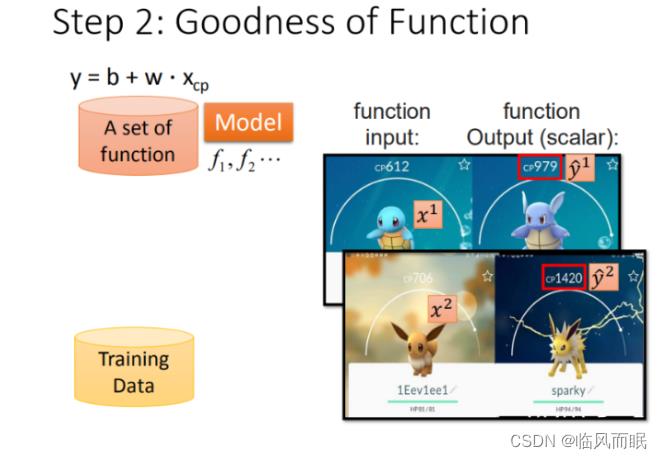
  • 这里定义 x 1 x^1 x1 是进化前的CP值， y ^ 1 \\haty^1 y^​1 进化后的CP值， ^ \\hat ^ 所代表的是真实值

  • 将10组原始数据在二维图中展示，图中的每一个点 $(x_cpn,\\hatyn) $ 对应着进化前的CP值 和 进化后的CP值

如何判断众多模型的好坏

  • 有了这些真实的数据，那我们怎么衡量模型的好坏呢？从数学的角度来讲，我们使用距离。求【进化后的CP值】与【模型预测的CP值】差，来判定模型的好坏。也就是使用损失函数（Loss function） 来衡量模型的好坏，统计10组原始数据 $\\left ( \\haty^n - f(x_cp^n) \\right )^2 $ 的和，和越小模型越好。如下图所示：

L ( f ) = ∑ n = 1 10 ( y ^ n − f ( x c p n ) ) 2 , 将 [ f ( x ) = y ] , [ y = b + w ⋅ x c p ] 代 入 = ∑ n = 1 10 ( y ^ n − ( b + w ⋅ x c p ) ) 2 \\beginaligned L(f)&=\\sum\\limits_n=1^10 (\\haty^n-f(x_cp^n))^2,将[f(x)=y],[y=b+w·x_cp]代入 \\\\&=\\sum\\limits_n=1^10(\\haty^n-(b+w·x_cp))^2\\endaligned L(f)​=n=1∑10​(y^​n−f(xcpn​))2,将[f(x)=y],[y=b+w⋅xcp​]代入=n=1∑10​(y^​n−(b+w⋅xcp​))2​

  • 最终定义 损失函数 Loss function：

    L ( w , b ) = ∑ n = 1 10 ( y ^ n − ( b + w ⋅ x c p ) ) 2 L(w,b)= \\sum_n=1^10\\left ( \\haty^n - (b + w·x_cp) \\right )^2 L(w,b)=n=1∑10​(y^​n−(b+w⋅xcp​))2

  • 图中每一个点代表着一个模型对应的 w w w 和 b b b

Step 3：最佳模型 - 梯度下降

  • 目标：筛选最优模型（参数 ω ， b \\omega，b ω，b）