动手实践丨基于ModelAtrs使用A2C算法制作登月器着陆小游戏

Posted 2022-12-13 华为云开发者联盟

摘要：在本案例中，我们将展示如何基于A2C算法，训练一个LunarLander小游戏。

本文分享自华为云社区《使用A2C算法控制登月器着陆》，作者：HWCloudAI 。

LunarLander是一款控制类的小游戏，也是强化学习中常用的例子。游戏任务为控制登月器着陆，玩家通过操作登月器的主引擎和副引擎，控制登月器降落。登月器平稳着陆会得到相应的奖励积分，如果精准降落在着陆平台上会有额外的奖励积分；相反地如果登月器坠毁会扣除积分。

A2C全称为Advantage Actor-Critic，在本案例中，我们将展示如何基于A2C算法，训练一个LunarLander小游戏。

整体流程：基于gym创建LunarLander环境->构建A2C算法->训练->推理->可视化效果

A2C算法的基本结构

A2C是openAI在实现baseline过程中提出的，是一种结合了Value-based (比如 Q learning) 和 Policy-based (比如 Policy Gradients) 的强化学习算法。

Actor目的是学习策略函数π(θ)以得到尽量高的回报。 Critic目的是对当前策略的值函数进行估计，来评价。

• Policy Gradients

Policy Gradient算法的整个过程可以看作先通过策略π(θ)让agent与环境进行互动，计算每一步所能得到的奖励，并以此得到一局游戏的奖励作为累积奖励G，然后通过调整策略π，使得G最大化。所以使用了梯度提升的方法来更新网络参数θ，利用更新后的策略再采集数据，再更新，如此循环，达到优化策略的目的。

• Actor Critic

agent在于环境互动过程中产生的G值本身是一个随机变量，可以通过Q函数去估计G的期望值，来增加稳定性。即Actor-Critic算法在PG策略的更新过程中使用Q函数来代替了G，同时构建了Critic网络来计算Q函数，此时Actor相关参数的梯度为：

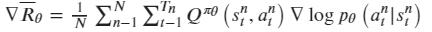
而Critic的损失函数使用Q估计和Q实际值差的平方损失来表示：

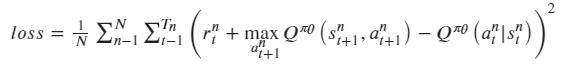
• A2C算法

A2C在AC算法的基础上使用状态价值函数给Q值增加了基线V，使反馈可以为正或者为负，因此Actor的策略梯变为：

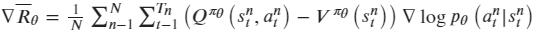
同时Critic网络的损失函数使用实际状态价值和估计状态价值的平方损失来表示：

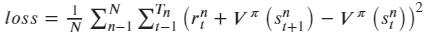
LunarLander-v2游戏环境简介

LunarLander-v2，是基于gym和box2d提供的游戏环境。游戏任务为玩家通过操作登月器的喷气主引擎和副引擎来控制登月器降落。

gym:开源强化学习python库，提供了算法和环境交互的标准API，以及符合该API的标准环境集。

box2d:gym提供的一种环境集合

注意事项

1. 本案例运行环境为 TensorFlow-1.13.1，且需使用 GPU 运行，请查看《ModelAtrs JupyterLab 硬件规格使用指南》了解切换硬件规格的方法；
2. 如果您是第一次使用 JupyterLab，请查看《ModelAtrs JupyterLab使用指导》了解使用方法；
3. 如果您在使用 JupyterLab 过程中碰到报错，请参考《ModelAtrs JupyterLab常见问题解决办法》尝试解决问题。

实验步骤

1. 程序初始化

第1步：安装基础依赖

要确保所有依赖都安装成功后，再执行之后的代码。如果某些模块因为网络原因导致安装失败，直接重试一次即可。

!pip install gym
!conda install swig -y
!pip install box2d-py
!pip install gym[box2d]

第2步：导入相关的库

import os
import gym
import numpy as np
import tensorflow as tf
import pandas as pd

2. 参数设置¶

本案例设置的 游戏最大局数 MAX_EPISODE = 100，保存模型的局数 SAVE_EPISODES = 20，以便快速跑通代码。

你也可以调大 MAX_EPISODE 和 SAVE_EPISODES 的值，如1000和100，可以达到较好的训练效果，训练耗时约20分钟。

MAX_EPISODE = 100 # 游戏最大局数
DISPLAY_REWARD_THRESHOLD = 100 # 开启可视化的reward阈值
SAVE_REWARD_THRESHOLD = 100 # 保存模型的reward阈值
MAX_EP_STEPS = 2000 # 每局最大步长
TEST_EPISODE = 10 # 测试局
RENDER = False # 是否启用可视化（耗时）
GAMMA = 0.9 # TD error中reward衰减系数
RUNNING_REWARD_DECAY=0.95 # running reward 衰减系数
LR_A = 0.001 # Actor网络的学习率
LR_C = 0.01 # Critic网络学习率
NUM_UNITS = 20 # FC层神经元个数
SEED = 1 # 种子数，减小随机性
SAVE_EPISODES = 20 # 保存模型的局数
model_dir = './models' # 模型保存路径

3. 游戏环境创建

def create_env():
    env = gym.make('LunarLander-v2')
 # 减少随机性
 env.seed(SEED)
    env = env.unwrapped
 num_features = env.observation_space.shape[0]
 num_actions = env.action_space.n
 return env, num_features, num_actions

4. Actor-Critic网络构建¶

class Actor:
 """
    Actor网络
    Parameters
    ----------
 sess : tensorflow.Session()
 n_features : int
 特征维度
 n_actions : int
 动作空间大小
 lr : float
 学习率大小
    """
 def __init__(self, sess, n_features, n_actions, lr=0.001):
 self.sess = sess
 # 状态空间
 self.s = tf.placeholder(tf.float32, [1, n_features], "state")
 # 动作空间
 self.a = tf.placeholder(tf.int32, None, "action")
 # TD_error
 self.td_error = tf.placeholder(tf.float32, None, "td_error")
 # actor网络为两层全连接层，输出为动作概率
 with tf.variable_scope('Actor'):
            l1 = tf.layers.dense(
                inputs=self.s,
                units=NUM_UNITS,
                activation=tf.nn.relu,
 kernel_initializer=tf.random_normal_initializer(0., .1),
 bias_initializer=tf.constant_initializer(0.1),
                name='l1'
 )
 self.acts_prob = tf.layers.dense(
                inputs=l1,
                units=n_actions,
                activation=tf.nn.softmax,
 kernel_initializer=tf.random_normal_initializer(0., .1),
 bias_initializer=tf.constant_initializer(0.1),
                name='acts_prob'
 )
 with tf.variable_scope('exp_v'):
 log_prob = tf.log(self.acts_prob[0, self.a])
 # 损失函数
 self.exp_v = tf.reduce_mean(log_prob * self.td_error)
 with tf.variable_scope('train'):
 # minimize(-exp_v) = maximize(exp_v)
 self.train_op = tf.train.AdamOptimizer(lr).minimize(-self.exp_v)
 def learn(self, s, a, td):
        s = s[np.newaxis, :]
 feed_dict = self.s: s, self.a: a, self.td_error: td
        _, exp_v = self.sess.run([self.train_op, self.exp_v], feed_dict)
 return exp_v
 # 生成动作
 def choose_action(self, s):
        s = s[np.newaxis, :]
        probs = self.sess.run(self.acts_prob, self.s: s) 
 return np.random.choice(np.arange(probs.shape[1]), p=probs.ravel())
class Critic:
 """
    Critic网络
    Parameters
    ----------
 sess : tensorflow.Session()
 n_features : int
 特征维度
 lr : float
 学习率大小
    """
 def __init__(self, sess, n_features, lr=0.01):
 self.sess = sess
 # 状态空间
 self.s = tf.placeholder(tf.float32, [1, n_features], "state")
 # value值 
 self.v_ = tf.placeholder(tf.float32, [1, 1], "v_next")
 # 奖励 
 self.r = tf.placeholder(tf.float32, None, 'r')
 # critic网络为两层全连接层，输出为value值
 with tf.variable_scope('Critic'):
            l1 = tf.layers.dense(
                inputs=self.s,
 # number of hidden units
                units=NUM_UNITS,
                activation=tf.nn.relu, 
 kernel_initializer=tf.random_normal_initializer(0., .1), 
 bias_initializer=tf.constant_initializer(0.1), 
                name='l1'
 )
 self.v = tf.layers.dense(
                inputs=l1,
 # output units
                units=1,
                activation=None,
 kernel_initializer=tf.random_normal_initializer(0., .1), 
 bias_initializer=tf.constant_initializer(0.1), 
                name='V'
 )
 with tf.variable_scope('squared_TD_error'):
 self.td_error = self.r + GAMMA * self.v_ - self.v
 # TD_error = (r+gamma*V_next) - V_eval
 self.loss = tf.square(self.td_error)
 with tf.variable_scope('train'):
 self.train_op = tf.train.AdamOptimizer(lr).minimize(self.loss)
 def learn(self, s, r, s_):
        s, s_ = s[np.newaxis, :], s_[np.newaxis, :]
        v_ = self.sess.run(self.v, self.s: s_)
 td_error, _ = self.sess.run([self.td_error, self.train_op],
 self.s: s, self.v_: v_, self.r: r)
 return td_error

5. 创建训练函数

def model_train():
    env, num_features, num_actions = create_env()
    render = RENDER
 sess = tf.Session()
    actor = Actor(sess, n_features=num_features, n_actions=num_actions, lr=LR_A)
    critic = Critic(sess, n_features=num_features, lr=LR_C)
 sess.run(tf.global_variables_initializer())
    saver = tf.train.Saver()
 for i_episode in range(MAX_EPISODE+1):
 cur_state = env.reset()
 cur_step = 0
 track_r = []
 while True:
 # notebook暂不支持该游戏的可视化
 # if RENDER:
 # env.render()
            action = actor.choose_action(cur_state)
 next_state, reward, done, info = env.step(action)
 track_r.append(reward)
 # gradient = grad[reward + gamma * V(next_state) - V(cur_state)]
 td_error = critic.learn(cur_state, reward,
 next_state)
 # true_gradient = grad[logPi(cur_state,action) * td_error]
 actor.learn(cur_state, action, td_error) 
 cur_state = next_state
 cur_step += 1
 if done or cur_step >= MAX_EP_STEPS:
 ep_rs_sum = sum(track_r)
 if 'running_reward' not in locals():
 running_reward = ep_rs_sum
 else:
 running_reward = running_reward * RUNNING_REWARD_DECAY + ep_rs_sum * (1-RUNNING_REWARD_DECAY)
 # 判断是否达到可视化阈值
 # if running_reward > DISPLAY_REWARD_THRESHOLD:
 #     render = True
 print("episode:", i_episode, "  reward:", int(running_reward), "  steps:", cur_step)
 break
 if i_episode > 0 and i_episode % SAVE_EPISODES == 0:
 if not os.path.exists(model_dir):
 os.mkdir(model_dir)
 ckpt_path = os.path.join(model_dir, '_model.ckpt'.format(i_episode))
 saver.save(sess, ckpt_path)

6. 开始训练

训练一个episode大约需1.2秒

print('MAX_EPISODE:', MAX_EPISODE)
model_train()
# reset graph
tf.reset_default_graph()

7.使用模型推理

由于本游戏内核可视化依赖于OpenGL，需要桌面化操作系统的窗口显示，但当前环境暂不支持弹窗，因此无法可视化，您可将代码下载到本地，取消 env.render() 这行代码的注释，查看可视化效果。

def model_test():
    env, num_features, num_actions = create_env()
 sess = tf.Session()
    actor = Actor(sess, n_features=num_features, n_actions=num_actions, lr=LR_A)
 sess.run(tf.global_variables_initializer())
    saver = tf.train.Saver()
 saver.restore(sess, tf.train.latest_checkpoint(model_dir))
 for i_episode in range(TEST_EPISODE):
 cur_state = env.reset()
 cur_step = 0
 track_r = []
 while True:
 # 可视化
 # env.render()
            action = actor.choose_action(cur_state)
 next_state, reward, done, info = env.step(action)
 track_r.append(reward)
 cur_state = next_state
 cur_step += 1
 if done or cur_step >= MAX_EP_STEPS:
 ep_rs_sum = sum(track_r)
 print("episode:", i_episode, "  reward:", int(ep_rs_sum), "  steps:", cur_step)
 break
model_test()
episode: 0   reward: -31   steps: 196
episode: 1   reward: -99   steps: 308
episode: 2   reward: -273   steps: 533
episode: 3   reward: -5   steps: 232
episode: 4   reward: -178   steps: 353
episode: 5   reward: -174   steps: 222
episode: 6   reward: -309   steps: 377
episode: 7   reward: 24   steps: 293
episode: 8   reward: -121   steps: 423
episode: 9   reward: -194   steps: 286

8.可视化效果

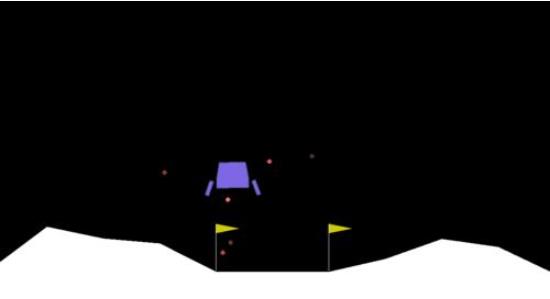
下面的视频为训练1000 episode模型的推理效果，该视频演示了在三个不同的地形情况下，登月器都可以安全着陆

https://modelarts-labs-bj4-v2.obs.cn-north-4.myhuaweicloud.com/course/modelarts/reinforcement_learning/a2c_lunarlander/A2C_lunarlander.mp4

点击关注，第一时间了解华为云新鲜技术~