图 学习笔记（11.21）

Posted 2022-12-13 未定_

最近数据结构和离散数学都学习了有关图的知识，自己学习算法也对图有了更加深入的了解，下面做一下汇总，便于复习翻看。(思路是自己理解写的，代码非原创)

---

图

• 一、图的概念
• 二、图的存储
• • 1.邻接矩阵
  • 2.邻接表
  • 3.链式前向星
• 三、最小生成树
• • 1.prim算法
  • 2.kruskal算法
• 四、最短路径
• • 1.Dijkstra算法
  • 2.Floyd算法
  • 3.Bellman-Ford算法
  • 4.SPFA算法
• 五、拓扑排序
• • 1.基于BFS的拓扑排序
  • • “无前驱”顶点优先
    • “无后继”顶点优先
  • 2.基于DFS的拓扑排序

---

一、图的概念

戳一戳->

二、图的存储

先补充两种图的遍历方式：


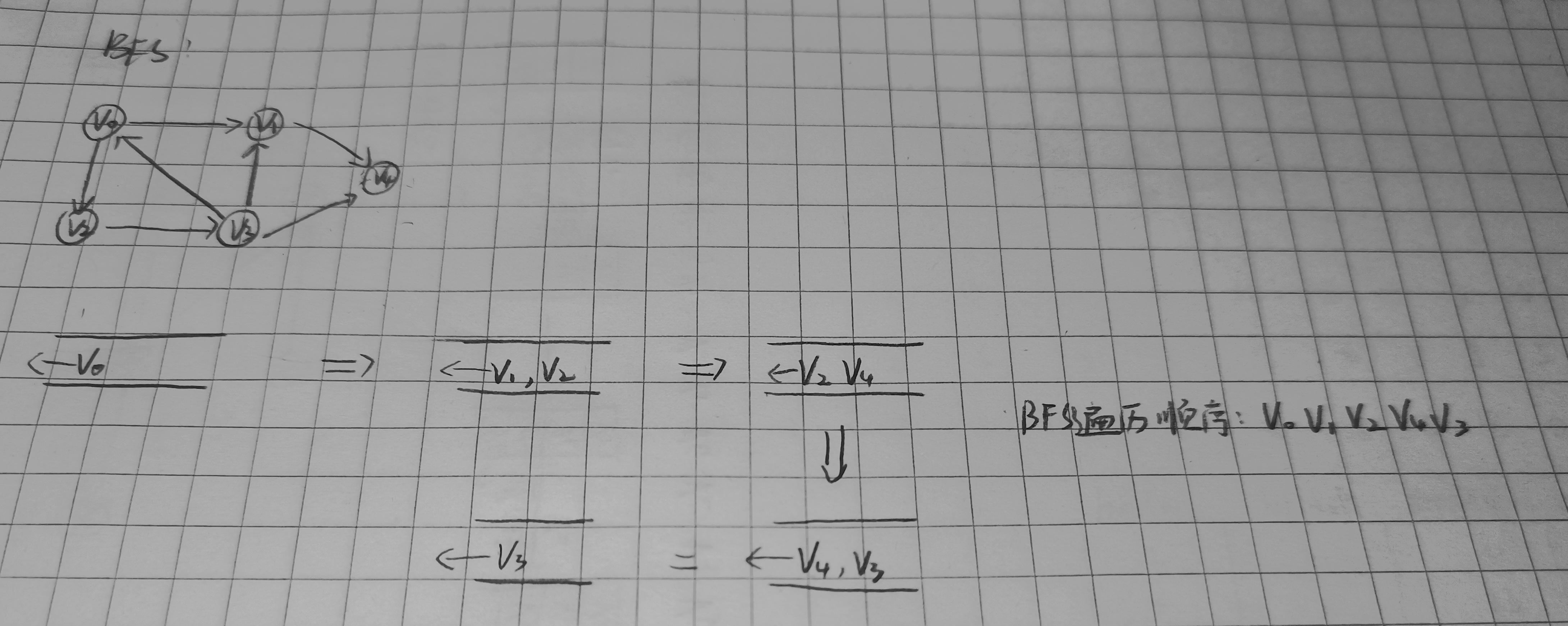
图的深度优先遍历类似于树的前序遍历，它所用到的数据结构是栈；图的广度优先遍历类似于树的
层序遍历，它所用到的数据结构是队列。

对任意一个图，从某顶点出发进行一次深度优先或广度优先遍历，可访问图的所有顶点。
【解答】错。只有连通图从某顶点出发进行一次遍历，可访问图的所有顶点。

1.邻接矩阵

思想：一个一维数组vertex[i]存顶点，一个二维数组edge[i][j]存边。
设图G=(V,E)有n个顶点，则邻接矩阵是一个n*n的方阵：
边无权值时，0表示顶点i和j之间无边，1表示有边：
$$edge[i][j]=\begin{array}{llc}0& & 若(v_i,v_j)\in E或<v_i,v_j>\in E\\ 1& & 否则\end{array}$$
边有权值时，w_ij表示顶点i到j的权值，0表示i=j，∞表示i和j之间无边：
$$edge[i][j]=\{\begin{array}{llc}{w}_{ij}& & 若(v_i,v_j)\in E或<v_i,v_j>\in E\\ 0& & 若i=j\\ \infty & & 否则\end{array}$$
无向图的邻接矩阵是对称矩阵，即edge[i][j]=edge[j][i]，有向图则不符合这个特点。邻接矩阵的主对角线为0，无向图中顶点i的度为第i行/列中非零元素的个数，有向图中顶点i的出度为第i行元素之和，入度为第i列元素之和。
注意：edge[i][j]中i和j代表顶点的顺序取决于vertex[i]中存储的顺序，如：vertex[4]=v₀,v₃,v₁,v₂，则edge[2][1]对应的边是(v₁,v₃)而不是(v₂,v₁)。
时间和空间复杂度O(n²)

边数等于邻接矩阵中非零元素个数的总和除以 2。

const int MaxSize=10;
int visited[MaxSize];
class Mgraph

public:
    Mgraph(int a[],int n,int e);//构造函数，建立n个顶点e条边的图
    ~Mgraph() 
    void DFSTraverse(int v);//深度优先遍历图
    void BFSTraverse(int v);//广度优先遍历图
private:
    int vertex[MaxSize];
    int edge[MaxSize][MaxSize];
    int vertexNum,edgeNum;//顶点数与边数
;
Mgraph::Mgraph(int a[],int n,int e)

    int i,j,k;
    vertexNum=n;
    edgeNum=e;
    for(i=0; i<vertexNum; i++)
        vertex[i]=a[i];//顶点数组赋值
    for(i=0; i<vertexNum; i++)
        for(j=0; j<vertexNum; j++)
            edge[i][j]=0;//边数组初始化
    for(k=0; k<edgeNum; k++) //给边赋值
    
        cin>>i>>j;
        edge[i][j]=1;
        edge[j][i]=1;//无向图，若想变成有向图，只需要删除本句
    

void Mgraph::DFSTraverse(int v)

    cout<<vertex[v];//访问顶点
    visited[v]=1;//置顶点被访问过
    for(int j=0; j<vertexNum; j++)
    
        if(edge[v][j]==1&&visited[j]==0)
            DFSTraverse(j);
    

void Mgraph::BFSTraverse(int v)

    int w,j,Q[MaxSize];
    int front=-1,rear=-1;
    cout<<vertex[v];//访问顶点
    visited[v]=1;//置顶点被访问过
    Q[++rear]=v;
    while(front!=rear)
    
        w=Q[++front];//队头元素出队
        for(j=0; j<vertexNum; j++)
        
            if(edge[w][j]==1&&visited[j]==0)
            
                cout<<vertex[j];
                visited[j]=1;
                Q[++rear]=j;
            
        
    

2.邻接表

顺序存储与链式存储相结合的表示图的一种方法。
思想：图的每个顶点v_i，将所有邻接于v_i的顶点链成一个单链表，称为顶点v_i的边表（有向图则称为出边表）
所有边表的头指针和存储顶点信息的一维数组构成了顶点表。如下图：

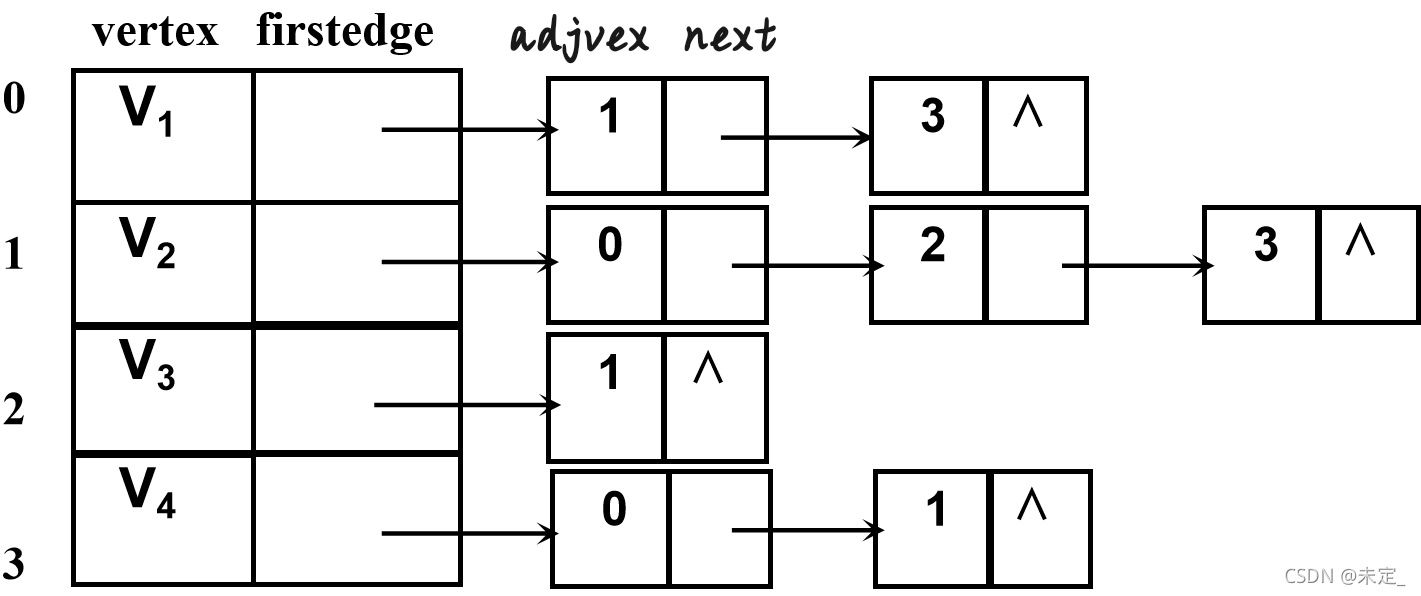
如果边有权值的话只需要在边表结构体里加一个变量info表示权值即可。

无向图中顶点i的边表中结点的个数为顶点i的度。
有向图中顶点 i 的出边表中结点的个数为顶点 i 的出度；各顶点的出边表中以顶点 i 为
终点的结点个数为顶点 i 的入度。

边数等于边表中的结点个数之和除以 2。

在无向图的邻接表中，顶点表有 n 个结点，边表有 2e 个结点，共有 n+2e 个结点，其空间复杂度
为Ｏ(n+2e)=Ｏ(n+e)。
时间和空间复杂度O(n+e)

const int MaxSize = 10;
struct EdgeNode//边表结点结构体

    int adjvex;//该顶点的邻接点在顶点表中的下标
    EdgeNode *next;
;
struct VertexNode//顶点表结点结构体

    int vertex;//存放顶点信息
    EdgeNode *firstEdge;//指向边表的第一个结点
;
int visited[MaxSize];
class ALGraph

public:
    ALGraph(int a[], int n, int e); //构造函数，建立n个顶点e条边的图
    ~ALGraph();
    void DFSTraverse(int v); //深度优先遍历图
    void BFSTraverse(int v); //广度优先遍历图
private:
    VertexNode adjlist[MaxSize]; //存放顶点表的数组
    int vertexNum,edgeNum;//顶点数和边数
;
ALGraph::ALGraph(int a[],int n,int e)

    int i,j,k;
    EdgeNode *s=NULL;
    vertexNum=n;
    edgeNum=e;
    for(i=0;i<vertexNum;i++)//初始化顶点表
    
        adjlist[i].vertex=a[i];
        adjlist[i].firstEdge=NULL;
    
    for(k=0;k<edgeNum;k++)
    
        cin>>i>>j;
        s=new EdgeNode;
        s->adjvex=j;
        s->next=adjlist[i].firstEdge;
        adjlist[i].firstEdge=s;//头插法
    

ALGraph::~ALGraph()

    EdgeNode *p=NULL,*q=NULL;
    for(int i=0;i<vertexNum;i++)
    
        p=q=adjlist[i].firstEdge;
        while(p!=NULL)
        
            p=p->next;
            delete q;
            q=p;
        
    

void ALGraph::DFSTraverse(int v)

    int j;
    EdgeNode *p=NULL;
    cout<<adjlist[v].vertex;
    visited[v]=1;
    p=adjlist[v].firstEdge; //工作指针p指向顶点v的边表
    while(p!=NULL)
    
        j=p->adjvex;
        if(visited[j]==0)
            DFSTraverse(j);
        p=p->next;
    

void ALGraph::BFSTraverse(int v)

    int w,j,Q[MaxSize];
    int front=-1,rear=-1;
    EdgeNode *p=NULL;
    cout<<adjlist[v].vertex;
    visited[v]=1;
    Q[++rear]=v;
    while(front!=rear)
    
        w=Q[++front];
        p=adjlist[w].firstEdge;
        while(p!=NULL)
        
            j=p->adjvex;
            if(visited[j]==0)
            
                cout<<adjlist[j].vertex;
                visited[j]=1;
                Q[++rear]=j;
            
            p=p->next;
        
    

vector实现邻接表

const int MaxSize = 10;
struct edge//边

    int from,to,w;//起点，终点，权值
    edge(int a,int b,int c)//对边赋值
    
        from=a;
        to=b;
        w=c;
    
;
vector<edge>e[MaxSize];//e[i]存第i个结点连接的所有边。
for(int i=1;i<=n;i++)//初始化
    e[i].clear();
e[a].push_back(edge(a,b,c));//存边
for(int i=0;i<e[u].size();i++)//检索结点u的所有邻居

    ...

3.链式前向星

例题

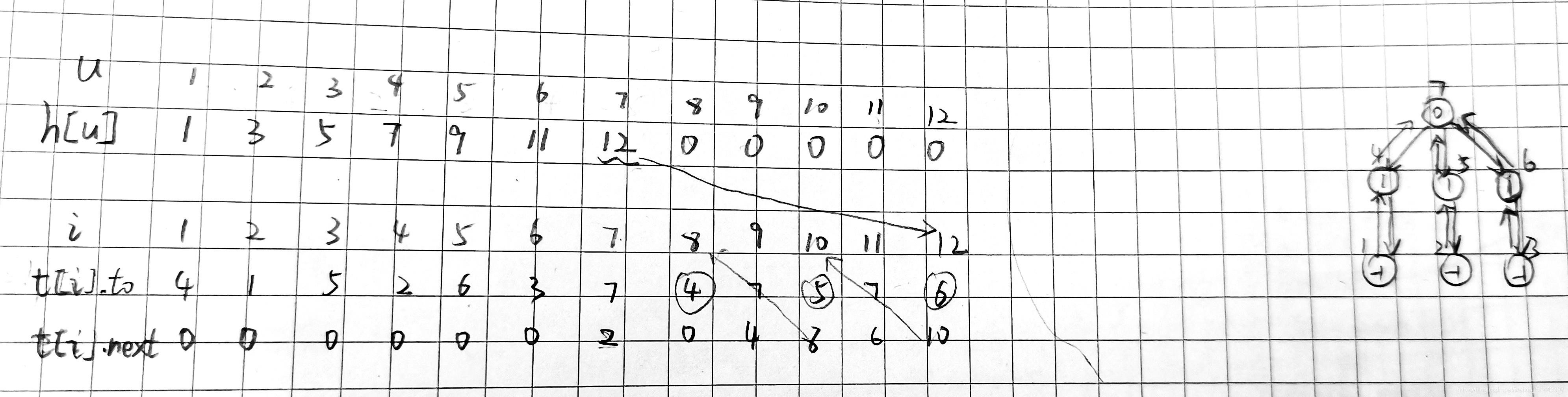
链式前向星存图如下：u表示结点，h[u]用来定位u的第一条边，t[i].to存u的邻居结点，t[i].next定位u的下一个邻居结点。例如：u=7时，h[u]=12，即结点7的第一条边连接的邻居结点存在i=12这个位置，t[12].to=6，表示结点7的第一个邻居是结点6，t[12].next=10,即结点7的第二条边连接的邻居结点存在i=10这个位置里，t[10].to=5，即结点7的第二个邻居结点是5，依次类推，直到t[i].next=0时停止。

const int N=16000;
struct n

    int to,next, w;
t[2*N];
int h[2*N],p=1;
void add(int u,int v,int w)

    t[p].to=v;
    t[p].w=w;
    t[p].next=h[u];
    h[u]=p++;

//遍历结点i的所有邻居
for(int  i=h[u];i;i=t[i].next)
...

其他存储方式：十字链表适合存储有向图，邻接多重表适合存储无向图。

三、最小生成树

连通图的生成树： 包含图所有顶点的极小连通子图
（注意：极小连通子图只存在于连通图中）
生成树的代价： 生成树上各边的权值之和称为生成树的代价。
图的生成树唯一性不能确定，n 个顶点的生成树有 n-1条边。

连通分量是无向图的极大连通子图，其中极大的含义是将依附于连通分量中顶点的所有边都加上，
所以，连通分量中可能存在回路。

最小生成树： 生成树中代价最小的。

对于含有 n 个顶点 e 条边的连通图，利用 Prim 算法求最小生成树的时间复杂度为O(n²)，利用 Kruskal算法求最小生成树的时间复杂度为O(elog₂e)。因为Prim 算法采用邻接矩阵做存储结构，适合于求稠密图的最小生成树；Kruskal 算法采用边集数组做存储结构，适合于求稀疏图的最小生成树。

1.prim算法

此方法对点进行贪心操作，设所有结点集合为V，再另设一个集合U用来存最小生