隐马尔可夫模型（HMM）

Posted 2022-12-13 Joe-Han

1. 背景知识

1.1随机过程

随机过程是随机变量的集合，其在随机变量的基础上引入时间的概念（可简单理解为随机变量关于时间的函数）。例如，$x_1(t),x_2(t),x_3(t),x_4(t)$ 都是时间的函数，我们将其称为样本函数，样本函数的集合便是一个随即过程。

其定义如下：设：$(Ω, F , P )$为一概率空间，集合$T$为一指标集合。如果对于所有$t ∈ T$，均有一随机变量$ξ_t (ω)$定义于概率空间$(Ω, F , P )$，则集合$\\beginBmatrix ξ_t (ω)|t ∈ T \\endBmatrix$为一随机过程。

1.2 马尔可夫性质

马尔可夫性质是概率论中的一个概念：当一个随机过程在给定现在状态及所有过去状态的情况下，其未来状态的条件概率分布仅依赖于当前状态，简而言之，随即过程中某状态的发生只取決它上一个时刻的状态，那么此随机过程即具有马尔可夫性质。数学上，如果$X（t）,t>0$为一个随机过程，则马尔可夫性质的定义如下：

• $Pr[X(t+h)=y|X(s)=x(s),s \\leqslant t] = Pr[X(t+h)=y|X(t)=x(t)], \\forall h >0$

一般来说，具备马尔可夫性质的随机过程是不具备记忆特质的。在这个系统中，现在的条件概率和过去及未来的状态都是独立且不相关的，具备马尔可夫性质的过程通常称为马尔可夫过程。

1.3 马尔可夫链

具备离散状态的马尔可夫过程，通常被称为马尔可夫链 。该过程中，在给定当前知识或信息的情况下，只有当前的状态用来预测将来，过去（即历史状态）对于预测未来（即当前之后的状态）是无关的。在马尔可夫链的每一步。系统根据概率分布，可以从一个状态变到另一个状态，也可以保持当前状态。状态的改变称为“迁移”，与不同的状态改变相关的概率称为“状态迁移概率”。马尔可夫链的典型例子包括：随即游走，PageRank算法。
下图给出了一个在两个状态间进行迁移的马尔可夫链模型示意图：

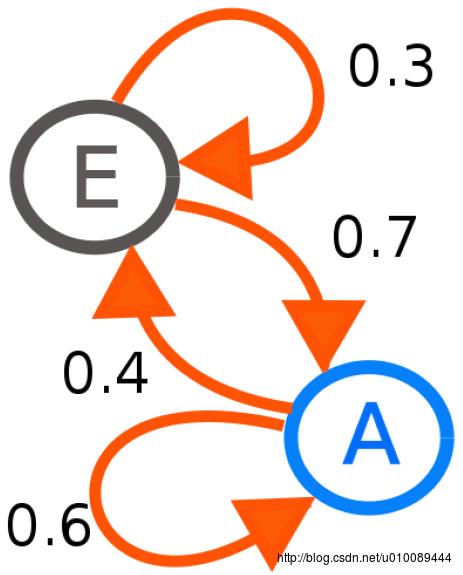
其数学定义如下：马尔可夫链是随机变量$X_1 , X_2 , X_3 , . . .$的一个数列。这些变量的范围，即它们所有可能取值的集合被称为“状态空间”，而$X_n$的值则是在时间n的状态。如果$X_｛n+1｝$对于过去状态的条件概率分布仅是$X_n$的一个函数，则：

• $P(X_n+1 = x | X_0,X_1,X_2,...,X_n) = P(X_n+1 = x | X_n)$

这里$x$为过程中的某个状态。上面这个等式也可看作马尔可夫性质的定义。

1.4 模式的形成

确定性模式：
考虑一套交通信号灯，灯的颜色变化序列依次是“红色→红色→黄色→绿色→黄色→红色”，如下图所示。

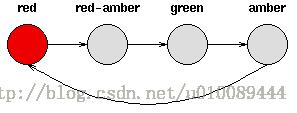
其中，每个状态都唯一地依赖于前一个状态。因此，如果当前交通灯为绿色，那么随后的交通灯颜色将只能是黄色，也就是说，该系统是确定性的。

非确定性模式：
马尔可夫链就是一种非确定性模式，状态之间的迁移不是确定的。下图给出了一阶天气状态变迁图，其中包含三个状态（晴天、雨天、多云），通过今天的天气状态可预测明天某天气状态出现的概率。

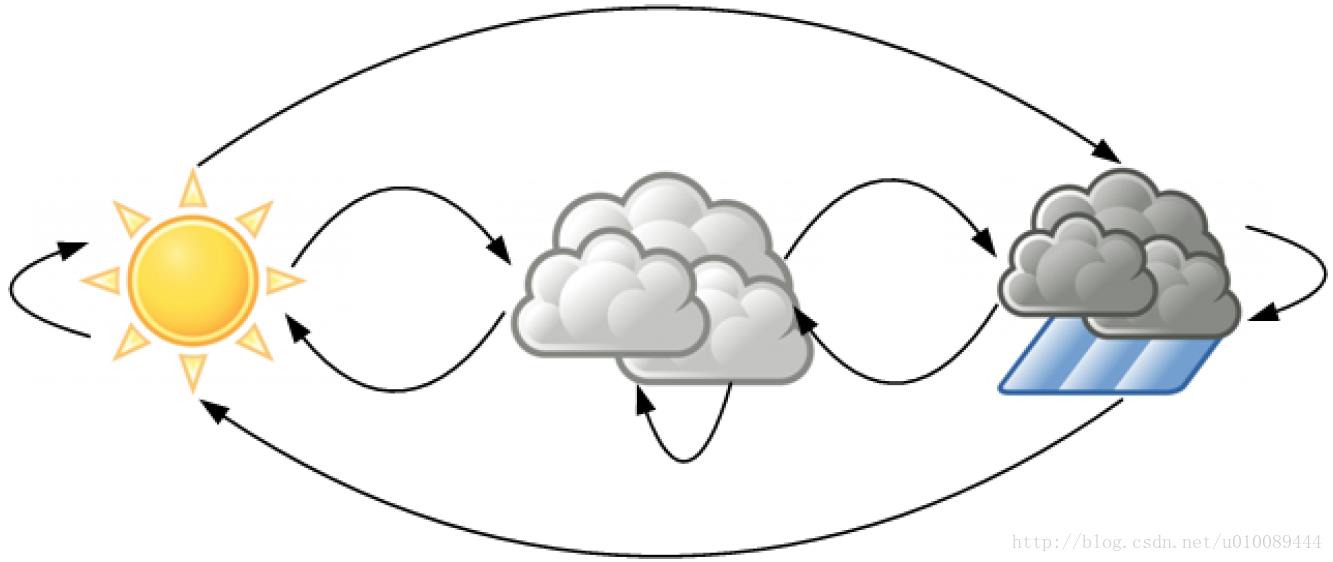
对于$M$个状态的一阶马尔可夫过程，共有$M^2$个状态转移，因为其中的每一个状态都可能是当前状态下一步迁移的目标，我们为每一个状态迁移事件关联一个概率值，称为状态迁移概率。下面的状态转移矩阵显示的是天气例子中可能的状态迁移概率。

可见，如果今天是晴天，那么明天是晴天的概率为0.5，多云的概率为0.375，下雨的概率为0.125。该过程假设概率值不随时间发生变化。

2. 隐马尔可夫模型

首先用参考资料中一个简单的例子来阐述：假设我手里有三个不同的骰子。第一个骰子是我们平常见的骰子（称这个骰子为D6），6个面，每个面（1，2，3，4，5，6）出现的概率是1/6。第二个骰子是个四面体（称这个骰子为D4），每个面（1，2，3，4）出现的概率是1/4。第三个骰子有八个面（称这个骰子为D8），每个面（1，2，3，4，5，6，7，8）出现的概率是1/8。

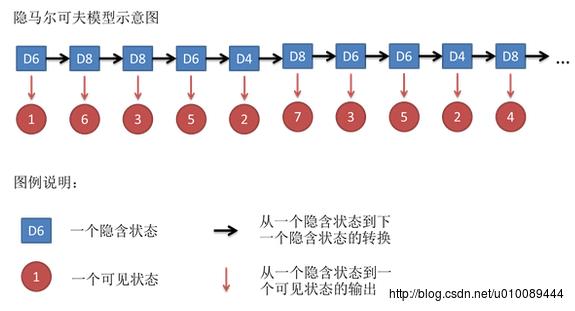
假设我们开始掷骰子，我们先从三个骰子里挑一个，挑到每一个骰子的概率都是1/3。然后我们掷骰子，得到一个数字，1，2，3，4，5，6，7，8中的一个。不停的重复上述过程，我们会得到一串数字，每个数字都是1，2，3，4，5，6，7，8中的一个。例如我们可能得到这么一串数字（掷骰子10次）：1 6 3 5 2 7 3 5 2 4。这串数字叫做可见状态链。但是在隐马尔可夫模型中，我们不仅仅有这么一串可见状态链，还有一串隐含状态链。在这个例子里，这串隐含状态链就是你用的骰子的序列。比如，隐含状态链有可能是：D6 D8 D8 D6 D4 D8 D6 D6 D4 D8。

一般来说，HMM中说到的马尔可夫链其实是指隐含状态链，因为隐含状态（骰子）之间存在转换概率（transition probability）。在我们这个例子里，D6的下一个状态是D4，D6，D8的概率都是1/3。D4，D8的下一个状态是D4，D6，D8的转换概率也都一样是1/3。这样设定是为了最开始容易说清楚，但是我们其实是可以随意设定转换概率的。比如，我们可以这样定义，D6后面不能接D4，D6后面是D6的概率是0.9，是D8的概率是0.1。这样就是一个新的HMM。

同样的，尽管可见状态之间没有转换概率，但是隐含状态和可见状态之间有一个概率叫做输出概率（emission probability）。就我们的例子来说，六面骰（D6）产生1的输出概率是1/6。产生2，3，4，5，6的概率也都是1/6。我们同样可以对输出概率进行其他定义。比如，我有一个被赌场动过手脚的六面骰子，掷出来是1的概率更大，是1/2，掷出来是2，3，4，5，6的概率是1/10。

2.1马尔可夫过程的局限性

回到天气的例子，实际情况中，观察者无法直接获取天气状况的观测值，但他们手中有一些海藻，民谚告诉我们，海藻的状态或许与天气的状态有密切的关系。由此我们得到了两种状态：可观测状态（海藻的干湿程度：dry，dryish，damp，soggy），和隐含状态（天气状况：sunny，cloudy，rainy）。我们希望基于马尔可夫假设和海藻的状态设计出某种算法，从而实现在缺乏天气历史观测数据的情况下，对未来的天气情况进行预测。另一个更实际的例子是语音识别问题，一些语音识别系统的工作原理是将语音所对应的单词视为隐状态，而采集到的声音视为观测状态。

根据海藻的干湿程度的观测值，我们对天气的例子进行重新设计，下图给出了其对应的隐马尔可夫模型：

隐藏状态相互之间是关联的，隐藏状态和观察状态之间的链接表示：在当前马尔可夫过程所处的特定隐藏状态下，生成特定观测状态的概率。因此，对每个观测状态而言，在所有隐藏状态下观测到该状态的概率值之和应该为1，即$Pr(Obs|Sunny) + Pr(Obs|Cloudy) + Pr(Obs|Rainy)= 1$。由此，我们也可定义输出矩阵（Emission Matrix），又称为混淆矩阵（Confusion Matrix），该矩阵的元素为：给定隐藏状态，得到某一观测状态的可能性，如下图所示：

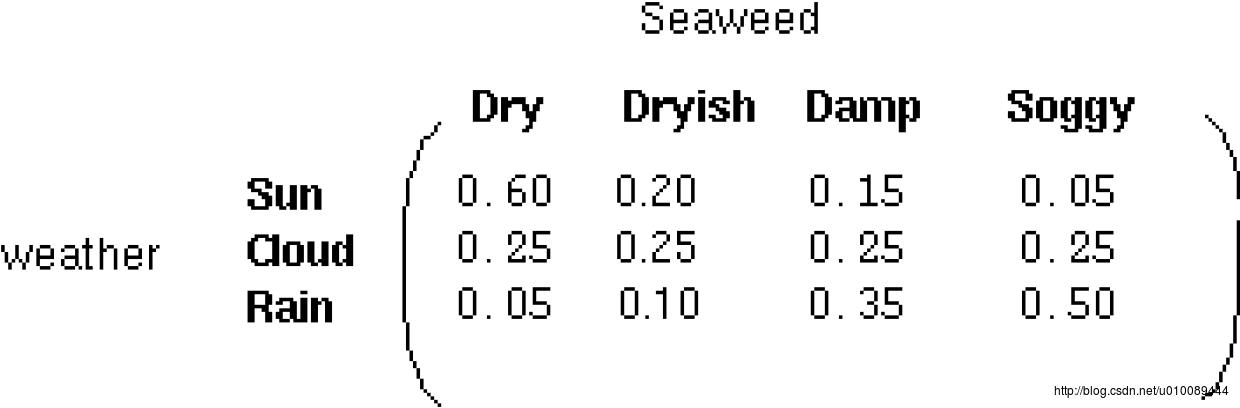
2.2 隐马尔可夫模型定义

隐马尔可夫模型（Hidden Markov Model，HMM）是一个统计模型，它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析，例如模式识别。在一般的马尔可夫模型中，状态对于观察者来说是直接可见的。这样状态的转换概率便是全部的参数。而在隐马尔可夫模型中，状态并不是直接可见的，但受状态影响的某些变量则是可见的。每一个状态在可能输出的符号上都有一个概率分布。因此输出符号的序列能够透露出状态序列的一些信息。

一个隐马尔可夫过程是一个三元组$（\\Pi ,A,B）$: