杨辉三角的解法

Posted 2022-12-12 beordie.cloud

杨辉三角的解题方法

题目：给定一个非负索引 rowIndex，返回「杨辉三角」的第 rowIndex 行。在「杨辉三角」中，每个数是它左上方和右上方的数的和。

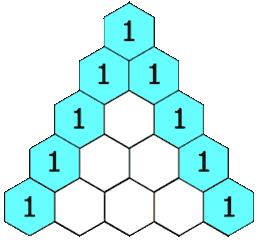
解法一

 按照杨辉三角的定义，将每一层的数据都进行计算保存，然后返回最后一层的数据据即可，需要第 N 层就需要一个 N 维的二维数组。其中 第零层 和 第一层 是比较特殊的，需要进行单独的定义，其余层按照规则进行生成。

class Solution 
    public List<Integer> getRow(int rowIndex) 
        List<List<Integer>> ret = new ArrayList();
        if(rowIndex >= 0) 
            List<Integer> ans = new ArrayList();
            ans.add(1);
            ret.add(ans);
        
        if(rowIndex >= 1) 
            List<Integer> ans = new ArrayList();
            ans.add(1);
            ans.add(1);
            ret.add(ans);
        
        for(int i = 2; i <= rowIndex; i++) 
            List<Integer> temp = ret.get(i - 1);
            List<Integer> ans = new ArrayList();
            ans.add(1);
            for(int j = 0; j + 1 < temp.size(); j++) 
                ans.add(temp.get(j) + temp.get(j + 1));
            
            ans.add(1);
            ret.add(ans);
        
        return ret.get(rowIndex);
    

解法二

 解法一每层都重新开辟空间来进行存储，浪费了大量的内存空间。观察整个计算的流程，其实只用到了上一层的数据和下一层的存储空间，也就是只需要两层的空间即可完成最终数据的计算。也就是可以设计一个滚动的两层空间来进行计算存储，区分上一层和当前的计算层，上一层用 减一模二 来代替下标，当前计算层直接 模二 。

 一维数组的大小的话直接设置为输出层的长度，也就是 rowIndex + 1 。

class Solution 
    public List<Integer> getRow(int rowIndex) 
        int[][] ret = new int[2][rowIndex + 1];
        ret[0][0] = 1;
        for(int i = 1; i <= rowIndex; i++) 
            int preIndex = (i - 1) % 2, index = i % 2;
            ret[index][0] = 1;
            for(int j = 1; j <= i; j++) 
                ret[index][j] = ret[preIndex][j - 1] + ret[preIndex][j];
            
        
        return Arrays.stream(ret[rowIndex % 2]).boxed().collect(Collectors.toList());
    

解法三

 再次观察整个图形的成型状况，可以将递推规则换一下思路，在每一层的前面添加一个 1 ，作为新增数据，需要变动的数据范围是除掉前后端点的两个值，更新当前的位置数据为加上下一个位置的值的和，这样只需要一个动态数组即可完成，也可以使用一个定长 rowIndex 数组从后面开始遍历。

class Solution 
    public List<Integer> getRow(int rowIndex) 
        LinkedList<Integer> ret = new LinkedList();
        if(rowIndex >= 0) ret.add(1);
        if(rowIndex >= 1) ret.add(1);
        for(int i = 2; i <= rowIndex; i++) 
            ret.addFirst(1);
            for(int j = 1; j < ret.size() - 1; j++) 
                ret.set(j, ret.get(j) + ret.get(j + 1));
            
        
        return ret;