二分查找——一网打尽所有细节！

Posted 2022-12-11 rotk2015

1. 二分查找，典中典的算法，为了便于说明，先给出测试样例：

   public static void main(String[] args) 
       int[] a = new int[]0,1,4,4,4,4,5;
       int index = search(a,4);
       System.out.println(index);
   
   

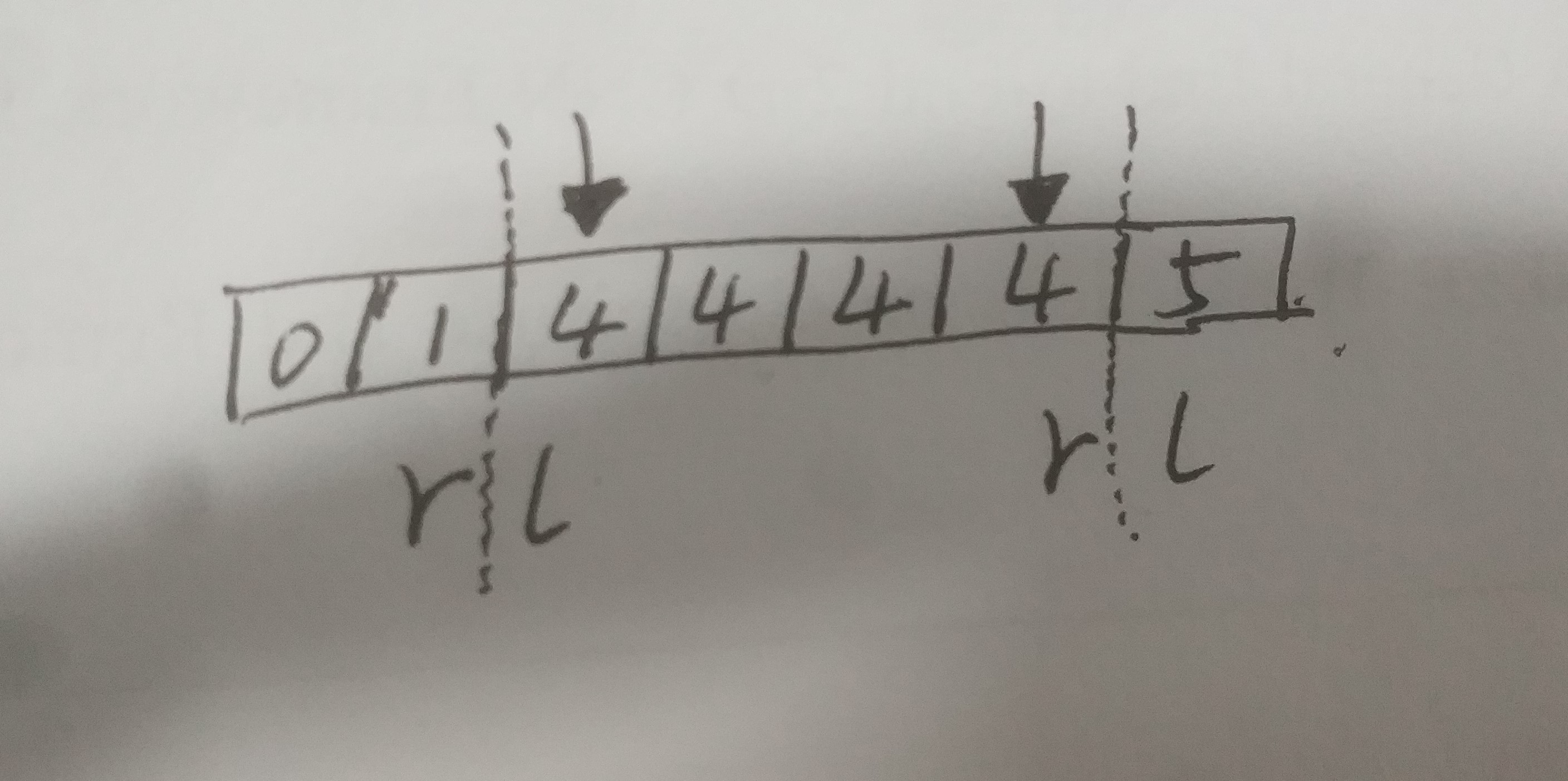
2. 对于元素 4，我们约定如下概念：左下界为1，下界为2，上界为5，右上界为6。

3. 查找下界的代码如下，这里采用了左闭右闭的写法：

   public static int search(int[] arr, int n)
       int l = 0, r = arr.length - 1;
       int mid;
       while(l <= r)
            mid = l + ((r-l)>>1);
           if(arr[mid] < n)
               l = mid + 1;
           else
               r = mid - 1;
       
       return l;
   
   

   需要注意的点：由于按左闭右闭初始化 l、r，因此循环控制条件应是 <= ，即，退出循环时，r 紧挨着 l 位于其左边（一定要仔细体会这句话，这是这种写法的关键），故函数返回值需要按要求决定是 l 或 r。

   此外，我们约定，当前元素为 arr[mid]，目标元素为 形参 n。

4. 

5. 对于二分查找，目前还未讨论的就剩下边界（l 和 r）的移动方式，以及当前元素等于目标元素时的处理方式了。

6. 仔细观察 4 中的图，对于查找下界这种情况而言，左边界 l 最终指向的可能还是目标元素，但右边界 r，它可是要向左跳过所有目标元素的边界啊！因此，若当前元素等于目标元素，我们无法动左边界 l，只能（也是必须）将右边界 r 向左移动1格（即 r=mid-1）。此外，若想查找左下界，只需返回值由 l 改为 r 即可。

7. 同理，对于查找上界这种情况而言，右边界 r 最终指向的可能还是目标元素，但左边界 l，要向右跳过所有目标元素。故，此时若当前元素等于目标元素，我们无法动右边界 r，只能（也是必须）将左边界 l 向右移动1格（即 l=mid+1）。此时，仅需将 if 判断条件里的 < 改为 <=，函数返回值改为 r 即可。对于查找右上界，易知返回 l。

8. 若目标元素不存在（这也是为什么在上文中要说可能），那么无论 if 判断条件里是 < 还是 <=，都不影响结果，此时，示意图中的两条虚线会重合，影响结果的只是函数返回值。