数控技术 - 直线插补 - 逐点比较法

Posted 2022-12-11 L建豪 忄YH

数控技术-直线插补 - 逐点比较法

前言：还有5天要考《数控技术》了，开始（复习）预习时发现，考点之一是直线插补。这个知识点不是我上个学期的课程设计——运动控制卡的主要功能之一吗。我当时对直线插补的理解还是很简单的：一边两点取中间打折，使线段更加平滑。现在看了理论实现后发现，可以说不是一个东西了，所以甚是感觉有趣。

排除掉要应付大学考试，直线插补这个知识点还是很主要的。特地写篇笔记记录，防止以后忘记。

• 推荐视频：《逐点比较法-478-机床数控系统综合设计-远程教育|夜大|面授|函授|家里蹲大学|宅在家|在家宅_哔哩哔哩_bilibili》北京理工大学老师讲解，up主应该是转载或代传。

1.解释

• 逐点比较法，顾名思义，逐个点比较。每次进给都会得到一个点，然后再和目标线段比较误差。根据误差决定下一次进给的方向，循环反复。
• 该方法有个重要定义：只适用于两轴决定的平面，每次进给都只能沿轴方向，必须且只能选一个轴方向。

数学定义很重要，嗯……

• 下面直接看效果图，图源自网络 。实践时，XY轴就是电机控制，每次移动一定单位量。

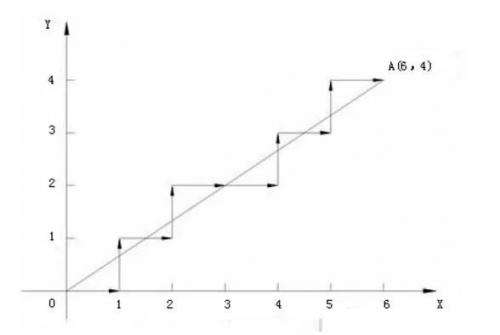
2.过程步骤

• 根据视频教程的总结，可访分为5步：①得出偏差函数；②偏差判别；③坐标进给；④新的偏差计算；⑤终点判别，如果没到就重复②，循环反复；

（0）符号

• 为下面的内容做些规定，用符号代替名词，方便阅读。

1. 原点 O；

$$(x_s,y_s)$$

2. 终点 E ；

$$(x_e,y_e)$$

3. 中间点 P；（ij表示各轴进给的次数）

$$(x_i,y_j)$$

（1）公式由来

• 因为进给是单位量，所以得到的中间点P会出现3种情况：在线段上方，在线段中，在线段下方。
• 逐点比较法的重点是 比较偏差 ，为了方便，定义用斜率比较偏差。

下面公式例子 部分 只列举一种情况，排版原因不穷举了。

• 用线段OP的斜率与OE比较：斜率大，在线段上方；斜率 相等 ，在线段中；斜率小，在线段下方。

$$\frac{y_j}{x_i}>\frac{y_e}{x_e}$$

• 数学式子要漂亮，为了方便计算，化简成与零作比较。

$$y_i\ast x_e-y_e\ast x_i>0$$

• 这个式子就定义为偏差函数，决定了进给方向。

$$F=x_e\ast y_j-x_i\ast y_e>0$$

• 结合第一象限的图，点P位于线段下方时，进给就要 向上 ，靠近线段；位于线段上方时，进给就要 向前 ，靠近线段。即分别沿y轴正方向，x轴正方向进给。同时规定，在线段中时，也属于线段上方，沿x轴进给。

$$(+\Delta x)$$

• 计算新的偏差函数，然后整理化简可得，新的偏差就等于，上一个偏差减去点E的y轴坐标，或上一个偏差加上点E的x轴坐标。

$$\begin{gathered} F_1=x_e\ast y_j-(x_i+1)\ast y_e=(x_e\ast y_j-x_i\ast y_e)-y_e=F-y_e \\ {F}_1=x_e\ast (y_j+1)-x_i\ast y_e=(x_e\ast y_j-x_i\ast y_e)+x_e=F+x_e \end{gathered}$$

• 到这里就很明朗了，我只需计算初始的偏差函数，然后每次新的偏差函数根据终点E坐标和进给方向计算。无须在意中间点P的坐标。巧妙啊！

$$\begin{gathered} F_1=F-y_e \\ {F}_1=F+x_e \end{gathered}$$

• 关于终点的判别，有2种方法：总步长法、总坐标法。原理都一样，其实得到轨迹图后分开xy轴，会发现就是在走 三角形 。比如走到点(x_s,y_e)再走到点(x_e,y_e)，所以，其实只要总步数够了一定能到达终点。

$$N=|x_e|+|y_e|$$

• 又或者，只要三角形的最长边已经走完了，也代表已经走到终点了。

3.例题

最后还是要做个题目练练手，不能转头就忘记了。

题目：加工第一象限直线OE，起点为坐标原点，终点坐标为E（6，3），试用逐点比较法对该段直线进行插补，并画出插补轨迹。

1. 偏差函数

$$F=x_e\ast y_i-x_i\ast y_e=6\ast 0-0\ast 3=0$$

2. 偏差判别

$$F=0$$

3. 坐标进给

$$(+\Delta x)$$

4. 偏差计算

F 1 = F − y e = − 3 F_1 = F - y_e = -3 以上是关于数控技术 - 直线插补 - 逐点比较法的主要内容，如果未能解决你的问题，请参考以下文章

数控技术 - 直线插补 - 逐点比较法

菜鸟学四轴控制器之2:逐点比较法

Android开发-根据起点终点实现直线逐点绘制动画-02

Android开发-根据起点终点实现直线逐点绘制动画-01

数控技术 - 直线插补 - 数字积分法（DDA）

数控技术 - 直线插补 - 数字积分法（DDA）