立体视觉入门指南:关键矩阵(本质矩阵,基础矩阵,单应矩阵)
Posted 李迎松~
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了立体视觉入门指南:关键矩阵(本质矩阵,基础矩阵,单应矩阵)相关的知识,希望对你有一定的参考价值。
亲爱的同学们,我们的世界是3D世界,我们的双眼能够观测三维信息,帮助我们感知距离,导航避障,从而翱翔于天地之间。而当今世界是智能化的世界,我们的科学家们探索各种机器智能技术,让机器能够拥有人类的三维感知能力,并希望在速度和精度上超越人类,比如自动驾驶导航中的定位导航,无人机的自动避障,测量仪中的三维扫描等,都是高智机器智能技术在3D视觉上的具体实现。
立体视觉是三维重建领域的重要方向,它模拟人眼结构用双相机模拟双目,以透视投影、三角测量为基础,通过逻辑复杂的同名点搜索算法,恢复场景中的三维信息。它的应用十分之广泛,自动驾驶、导航避障、文物重建、人脸识别等诸多高科技应用都有它关键的身影。
本课程将带大家由浅入深的了解立体视觉的理论与实践知识。我们会从坐标系讲到相机标定,从被动式立体讲到主动式立体,甚至可能从深度恢复讲到网格构建与处理,感兴趣的同学们,来和我一起探索立体视觉的魅力吧!
本课程是电子资源,所以行文并不会有太多条条框框的约束,但会以逻辑清晰、浅显易懂为目标,水平有限,若有不足之处,还请不吝赐教!
个人微信:EthanYs6,加我申请进技术交流群 StereoV3D,一起技术畅聊。
CSDN搜索 :Ethan Li 李迎松,查看网页版课程。
随课代码,将上传至github上,地址:StereoV3DCode:https://github.com/ethan-li-coding/StereoV3DCode
大家好,上一篇立体视觉入门指南(1):坐标系与相机参数中,我们对立体视觉的基础坐标系做了详细的介绍,承接上篇,本篇我们继续来讲基础:关键矩阵。
矩阵运算是立体视觉最常见的数学工具了,在前一篇中,相机的内参和外参也都是以矩阵的形式描述,我认为大家都有了一定的基础,线性代数和矩阵论都有涉猎,万一没有,那只能建议你们补补基础课了。
在双目视觉中,两个图像之间会有公共区域,自然地大家会想到这些公共区域的点是否会存在一些联系,更具体地是它们的坐标是否存在一些约束关系,比如关于它们坐标的关系式是否满足某个条件等式,抑或能否直接将某张图像上的点坐标转换成另一个图像上的点坐标。幸运的是,答案都是肯定的。本篇即为大家介绍双目视觉中三个关键的矩阵:本质矩阵、基础矩阵、单应性矩阵,它们可以建立两个视图公共点之间的坐标联系,或者完成公共点之间的坐标转换。它们就像立体视觉双视图之间的桥梁,让彼此紧密相连,形成一个整体,才算有了立体视觉系统的概念。
大家想必会发现,在上一篇中所介绍的坐标系知识,都是针对于单个相机而言,那么双目该如何考虑呢?双目视觉又是如何形成的呢?
首先让我们从人眼出发,我们之所以能够感受周围的立体世界,正是因为人的双眼形成了双目立体,同一个物体在两只眼睛内同时成像,由三角原理可以得到物体的三维空间坐标。
双目立体系统的结构和人眼类似,由两个相机组成,它们的视场相互重叠,重叠区域的场景可以通过寻找在两个相机上各自的成像点,并基于三角测量原理计算空间三维坐标。从硬件上来说,单目到双目只是多了一个相机(广义上来说,同一个相机移动到两个不同的位置也形成双目立体系统,这里以两个相机为角度展开);从系统上来说,要形成一个系统,就需要双相机之间建立一条让两者紧密相连的纽带。上一课我们描述了单相机的几个重要的坐标系,显然,双相机都会有各自的独立坐标系统,而这条纽带就是建立在各自的独立坐标系统之间,而哪还有比以相机中心为原点的三维相机坐标系更适合这个角色的呢?因此,在双目立体系统中,在双相机的相机坐标系之间建立一个旋转和平移转换关系,也就是熟知的外参矩阵 R R R 和 t t t ,直观上来说,它们将空间点在左相机的相机坐标系坐标转换为在右相机的相机坐标系坐标,实质上,它们是描述两个相机的相对位姿关系,让两者紧密相连,互为彼此。如下图为一个典型的双目结构图。
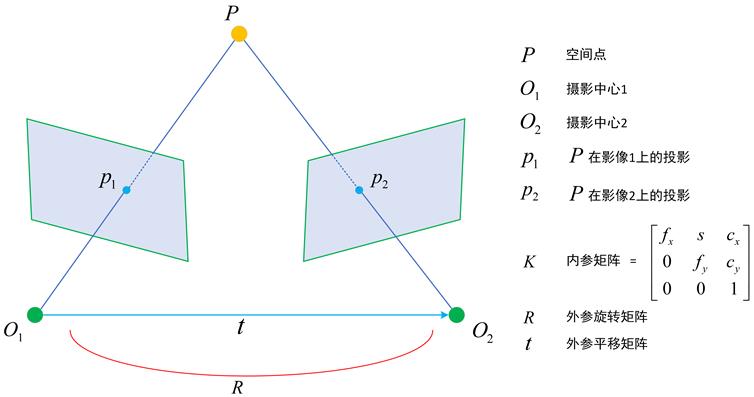
对于
R
R
R和
t
t
t,我们给出纯数学上的描述,假设空间点P在左相机相机坐标系下的坐标为
P
P
P,在右相机相机坐标系下的坐标为
P
′
P'
P′,则满足:
P
′
=
R
∗
P
+
t
P'=R*P+t
P′=R∗P+t
除此之外,还通常会将双目系统的世界坐标系放在左相机的中心,并和左相机坐标系完全重合,从这个角度来说, R , t R,t R,t就相当于是右相机在世界坐标系下的外参,而左相机在世界坐标系的外参则是 I , 0 I,0 I,0( I I I为单位阵)。
以上便是双目立体系统双相机之间的坐标系联系,但不能忽视的是,这些坐标系似乎并不那么直接,在实际应用中,我们最先接触的可不是虚拟在脑海中的坐标系,而是呈现在眼前亦或存储在计算机内存中的图像!图像像素和像素的像点坐标,才是最直观的输入信息。所以,是否存在像素坐标之间的紧密联系呢?答案是有,也便是本篇的内容:关键矩阵,正是描述像素坐标之间的紧密联系。
文章目录
本质矩阵和基础矩阵
设空间点P在左相机坐标系坐标的坐标为
P
P
P,则在右相机坐标系中的坐标为
R
P
+
t
RP + t
RP+t,其在左右相机视图中的投影点分别为
p
1
,
p
2
p_1,p_2
p1,p2。基于相机坐标系到影像坐标系的转换公式,得到如下转换式:
d
1
p
1
=
K
1
P
,
d
2
p
2
=
K
2
(
R
P
+
t
)
d_1p_1=K_1P,d_2p_2=K_2(RP+t)
d1p1=K1P,d2p2=K2(RP+t)
左边的
p
p
p是齐次坐标,如果对空间点也取齐次,即将空间点归一化到
Z
=
1
Z=1
Z=1的平面,
d
d
d 就变成了1,上式变成
p
1
=
K
1
P
,
p
2
=
K
2
(
R
P
+
t
)
p_1=K_1P,p_2=K_2(RP+t)
p1=K1P,p2=K2(RP+t)
该等式在齐次意义上成立,也就是乘以任意非零常数依旧相等。
咱们把
K
K
K拿到等式左边来,则公式变成:
K
1
−
1
p
1
=
P
,
K
2
−
1
p
2
=
R
P
+
t
K_1^-1p_1=P,K_2^-1p_2=RP+t
K1−1p1=P,K2−1p2=RP+t
设
x
1
=
K
1
−
1
p
1
,
x
2
=
K
2
−
1
p
2
x_1=K_1^-1p_1,x_2=K_2^-1p_2
x1=K1−1p1,x2=K2−1p2
可得
x
1
=
P
,
x
2
=
R
P
+
t
=
>
x
2
=
R
x
1
+
t
x_1=P,x_2=RP+t => x_2=Rx_1+t
x1=P,x2=RP+t=>x2=Rx1+t
两边同时叉乘
t
t
t,可得
t
×
x
2
=
t
×
R
x
1
+
t
×
t
t×x_2=t×Rx_1+t×t
t×x2=t×Rx1+t×t
矢量和自己叉乘等于0,因此 t × R x 1 = t × x 2 t×Rx_1=t×x_2 t×Rx1=t×x2,
再两边同时左乘
x
2
T
x_2^T
x2T,得
x
2
T
t
×
R
x
1
=
x
2
T
t
×
x
2
x_2^Tt×Rx_1=x_2^Tt×x_2
x2Tt×Rx1=x2Tt×x2
等式右边显然是等于0的,可得
x
2
T
t
×
R
x
1
=
0
x_2^Tt×Rx_1=0
x2Tt×Rx1=0
叉乘可以等价于用反对称矩阵来点乘,
t
t
t 的反对称矩阵表示为
t
t
t^,上式变成
x
2
T
t
∧
R
x
1
=
0
x_2^Tt^∧Rx_1=0
x2Tt∧Rx1=0
该式描述了像平面坐标
x
1
,
x
以上是关于立体视觉入门指南:关键矩阵(本质矩阵,基础矩阵,单应矩阵)的主要内容,如果未能解决你的问题,请参考以下文章