Codeforces Round #771 (Div. 2)（ABCDE）

Posted 2022-12-10 斗奋力努

Codeforces Round #771 (Div. 2)（ABCDE）

A. Reverse

题意：给一个长度为n的排序，可以翻转一次，使得字典序最小
思路：从前到后遍历，位置$i!=a[i]$,则翻转区间左端点i，右端点为值i所在位置

#include<bits/stdc++.h>
using namespace std;
const int N=505;
int n,a[N];

void solve()
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    int l=-1,r=-1;
    for(int i=1;i<=n;i++)
        if(a[i]==i) continue;
        else l=i;break;
    
    if(l==-1)
        for(int i=1;i<=n;i++) printf("%d ",i);
        puts("");
        return;
    
    if(l!=-1)
        for(int i=l+1;i<=n;i++)
            if(a[i]==l)r=i;break;
        
    
    for(int i=1;i<l;i++) printf("%d ",a[i]);
    for(int i=r;i>=l;i--) printf("%d ",a[i]);
    for(int i=r+1;i<=n;i++) printf("%d ",a[i]);
    puts("");


int main()
    int t;scanf("%d",&t);
    while(t--) solve();

B. Odd Swap Sort
题意：当两个$(a[i]+a[i+1])$时，可以交换两个值的位置，问最后是否可以使得序列为不降序列
思路：发现只能奇数和偶数交换，那么将奇数和偶数分开，初始奇数和偶数都为不降序列就yes，否则no

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,a[N];

void solve()
    vector<int>odd,even,odd1,even1;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
        if(a[i]%2==1) odd.push_back(a[i]);
        else even.push_back(a[i]);
    
    odd1=odd;even1=even;
    sort(odd.begin(),odd.end());
    sort(even.begin(),even.end());
    for(int i=0;i<odd.size();i++)
        if(odd[i]==odd1[i]) continue;
        else puts("NO");return;
    
    for(int i=0;i<even.size();i++)
        if(even[i]==even1[i]) continue;
        else puts("NO");return;
    
    puts("YES");


int main()
    int t;scanf("%d",&t);
    while(t--) solve();

C. Inversion Graph

题意：给长度为n的一种排列，每个逆序对可以连一根线，问最后有多少连通块
思路：从后往前，如果当前位置$i==a[i]$,那么就单独构成一个连通块，否则说明在左边(前面)区间$[1,i-1]$有一个位置$l$的数值为i。对于中间区间$[l,i]$。分类讨论，如果比$l$小，则更新$l$,如果比$l$大，则说明可以直接构成逆序对合成一个连通块，最后得到答案。

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,a[N];

void solve()
    int sum=0;
    map<int,int>mp;
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]),mp[a[i]]=i;
    for(int i=n;i>=1;)
        sum++;
        if(a[i]==i) i--;
        else
            int l=a[i],pos=i;
            while(pos>=l)
                if(pos==l)
                    if(a[pos]>l) i=pos-1;break;
                    else l=a[pos];
                
                else
                    if(a[pos]>=l) pos--;
                    else l=a[pos];
                
            
        
    
    printf("%d\\n",sum);


int main()
    int t;scanf("%d",&t);
    while(t--) solve();

D. Big Brush
题意：将一个nm的矩阵用22的矩阵染色，是否可以染色想要颜色，可以输出次数和染色方案，不可以输出-1
思路：倒过来想，每次去看哪些点可以染色，如果已经染成目标颜色，就将颜色清空变成"万能色",如果对未到达目标颜色的点$(i,j)$进行染色，当且仅当其负责的2*2矩阵中有”万能色“，或有颜色与之相同。最后还剩下颜色点就表示无法完成染色输出-1

#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int n,m,a[N][N];
bool vis[N][N];
int dx[]=-1,-1,-1,0,0,1,1,1;
int dy[]=-1,0,1,-1,1,-1,0,1;
struct nodeint x,y,col;;
vector<node>ans;

int merge(int &x,int y)
    if(x==y)return 1;
    if(x==0||y==0) x=x+y;return 1;
    return 0;


void cek(int x,int y)
    if(x<1||x>=n||y<1||y>=m) return;
    if(vis[x][y]) return;
    int color=a[x][y];
    if(!merge(color,a[x+1][y])) return;
    if(!merge(color,a[x][y+1])) return;
    if(!merge(color,a[x+1][y+1])) return;
    vis[x][y]=true;
    if(color) ans.push_back(x,y,color);
    a[x][y]=a[x+1][y]=a[x][y+1]=a[x+1][y+1]=0;
    for(int i=0;i<8;i++) cek(x+dx[i],y+dy[i]);


int main()
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            scanf("%d",&a[i][j]);
        
    
    for(int i=1;i<n;i++)
        for(int j=1;j<m;j++)
            cek(i,j);
        
    
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            if(a[i][j])
                puts("-1");
                return 0;
            
        
    
    int len=ans.size();
    printf("%d\\n",len);
    for(int i=len-1;i>=0;i--) printf("%d %d %d\\n",ans[i].x,ans[i].y,ans[i].col);
    return 0;

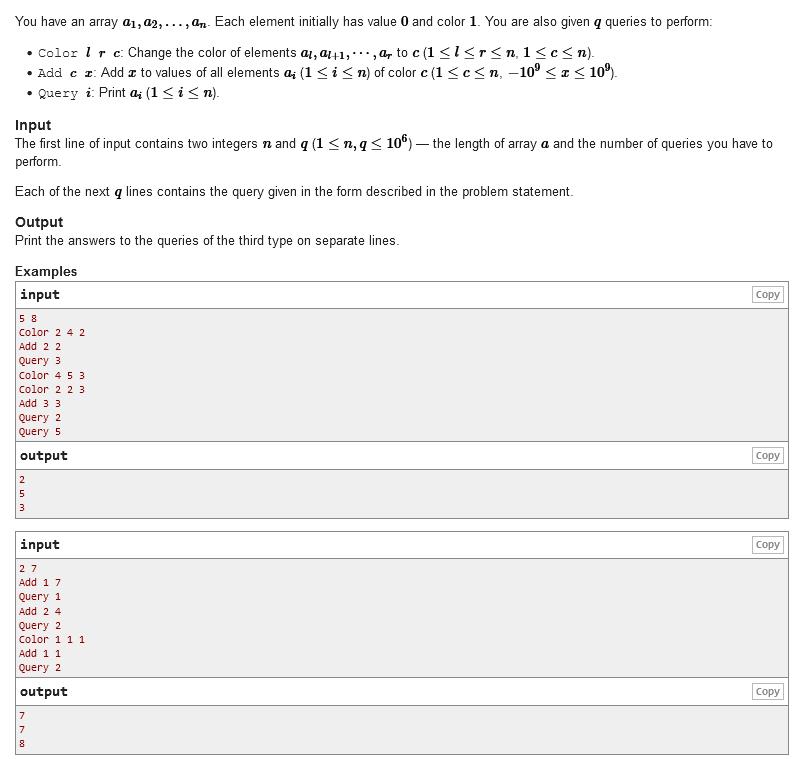
E. Colorful Operations
题意：
长度为n的序列，初始每个位置val=0,color=1
Color l,r,c: 区间[l,r]的颜色改成c
Add c x:所有颜色为c的位置val+=x
Query i:输出i位置的val
思路：
set记录每个区间的左端点，r[i]代表i所在区间的右端点，col[i]为i当前颜色，val[i]为颜色i的价值
tr[i]=val[i]-val[j] 每次改变颜色都先减去当前要变为颜色的当前值，最后算的时候加上当前颜色值就行了
同时用树状数组来记录单点的值

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=1e6+5;
ll n,q,val[N],color[N],R[N],tr[N];
set<ll>L;

ll lowbit(ll x)return x&(-x);

void insert(ll x,ll v)
    while(x<N)
        tr[x]+=v;
        x+=lowbit(x);
    


void seg(ll l,ll r,ll v)
    insert(l,v);
    insert(r+1,-v);


void Color(ll l,ll r,ll c)
    while(1)
        auto it=L.lower_bound(l);
        if(*it>r) break; //当前下一个区间与修改区间无交集
        if(R[*it]>r)//当前下一个区间左端点在修改区间内，右端点在修改区间外
            seg(*it,r,val[color[*it]]);
            R[r+1]=R[*it];
            color[r+1]=color[*it];
            L.erase(*it);
            L.insert(r+1);
        
        else//修改区间包含当前区间
            seg(*it,R[*it],val[color[*it]]);
            L.erase(*it);
        
    
    L.insert(l);
    R[l]=r;
    color[l]=c;
    seg(l,r,-val[c]);

    auto it=prev(L以上是关于Codeforces Round #771 (Div. 2)（ABCDE）的主要内容，如果未能解决你的问题，请参考以下文章
 
 Codeforces Round #771 (Div. 2)（ABCDE）
 Codeforces Round #771 (Div. 2)（ABCDE）
 Codeforces Round #771 (Div. 2) A~E
 Codeforces Round #771 (Div. 2) A~E
 Codeforces Round #771 (Div. 2) A~E
 Codeforces Round #436 E. Fire（背包dp+输出路径）