冒泡排序与快速排序

Posted 2022-12-08 Shemesz

两种交换排序算法

• 一、冒泡排序
• • 1. 代码展示
  • 2. 代码优化
  • 3. 时空分析
• 二、快速排序
• • 1. 代码展示
  • 2. 代码优化
  • 3.时空分析

  

交换排序

的基本思想是： 两两比较待排序记录的关键字，一旦发现两个记录不满足次序要求时，则进行交换，直到整个序列满足要求位置。在这里首先介绍基于简单交换思想实现的排序——冒泡排序，然后再此基础上进行改进的排序方法——快速排序。

一、冒泡排序

  冒泡排序（Bubble Sort） 一种最简单的交换排序方法，他通过比较两两比较相邻记录的关键字，如果发生逆序，则进行交换，从而使关键字小的记录如气泡般上浮，或者使关键字大的记录如石块一样逐渐下沉。

很形象的说明，两两比较，小的上浮，大的下沉，下面通过代码来观察一下具体实现吧！

1. 代码展示

#include <stdio.h>

#define ARR_LEN 255 /*数组长度上限*/
#define elemType int /*元素类型*/

/* 冒泡排序 */
/* 1. 从当前元素起，向后依次比较每一对相邻元素，若逆序则交换 */
/* 2. 对所有元素均重复以上步骤，直至最后一个元素 */
/* elemType arr[]: 排序目标数组; int len: 元素个数 */
void bubbleSort(elemType arr[], int len) 
    elemType temp;
    int i, j;
    int BJ=0, JH=0;      /*观察一下比较了多少次，交换了多少次*/
    for (i = 0; i < len - 1; i++) /* 外循环为排序趟数，len个数进行len-1趟 */
    
        for (j = 0; j < len - 1 - i; j++)/* 内循环为每趟比较的次数，第j趟比较len-1-i次 */
         
            BJ++;
            if (arr[j] > arr[j + 1]) /* 相邻元素比较，若逆序则交换（升序为左大于右，降序反之） */
            
                JH++;

                temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            
        
    
    printf("总共比较了%d次，总共交换了%d次\\n", BJ, JH);


int main(void) 
    elemType arr[ARR_LEN] =  3,5,1,-7,4,9,-6,8,10,4 ;
    int len = 10;
    int i;

    bubbleSort(arr, len);
    for (i = 0; i < len; i++)
        printf("%d\\t", arr[i]);
    putchar('\\n');

    return 0;

注意：冒泡排序就是把N个数进行N-1轮排序；升序排序中，大的数往下沉，小的往上浮；降序排序中，小的下沉，大的上浮

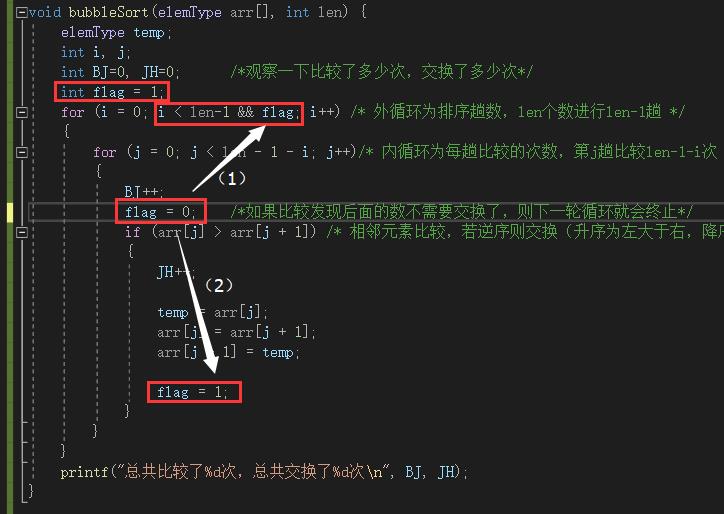
2. 代码优化

在代码运行过程当中会出现排序（N-1轮）未结束，但是序列已经不需要再排序，已经是排好序的状态了，但代码还是要按照流程走完比较余下序列的比较，这样计算机只是在做无用功而已，那么如何优化呢？直接上代码

定义 flag = 1

• （1）若在比较循环中 flag=0 标志位通过比较不需要进入交换语句当中，则 flag=0不符合外层循环条件，循环终止排序结束；
• （2）若通过比较发现需要交换，则在交换语句中继续通过flag=1的语句进入下一次循环的判断当中，直到排序结束

未优化之前45次，优化后35次

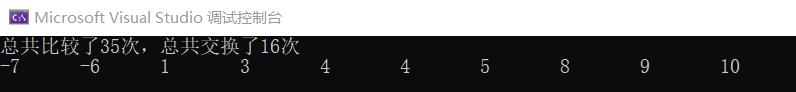
3. 时空分析

• 时间复杂度 O(n^2)
• 空间复杂度 O(1)
• 稳定排序

---

二、快速排序

  快速排序（Quick Sort） 是由冒泡排序改进而得的。在待排序的N个记录中，任意选取一个记录 （通常都为第一个）作为中枢轴（pivotkey）。经过一趟排序后，把所有关键字小于pivotkey的记录交换到左边（前面），把所有大于pivotkey的记录换到右边（后面），结果将排序分成两个子序列，最后将选中的pivotkey放到分界处的位置，然后分别对左、右子表重复上述过程，知道每个子表只有一个记录时排序完成。

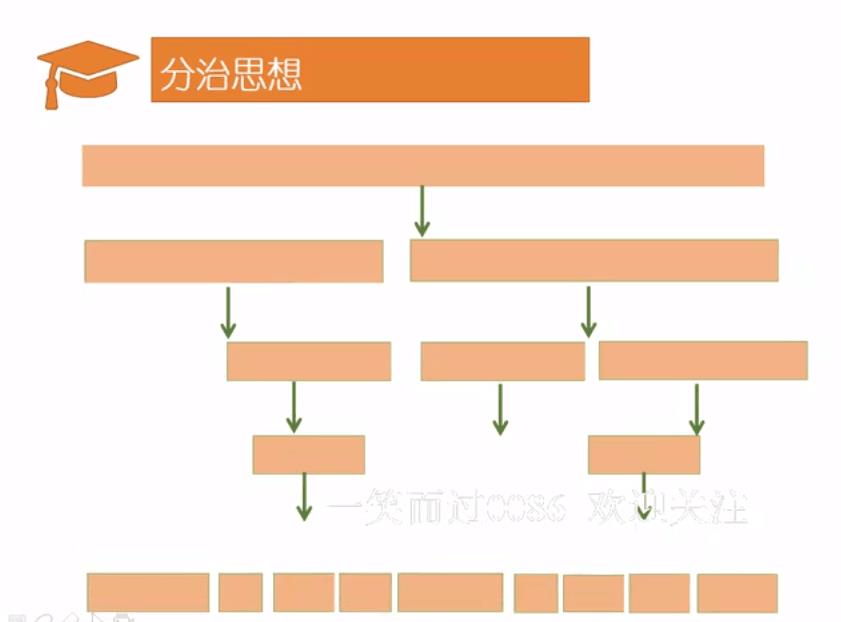
简单来说：

• 采用分治思想处理问题：将问题一直细化，知道解决能解决为止（后面通过展示即可理解）
  
• 通过递归函数实现快排：
  

原理展示： 原序数组（L：左下标 | R：右下标）

• 1）选第一个数为pivotkey
  
• 2）R指向的数与pivotb比较 ，发现小于pivot，则赋值给L的位置
  
  
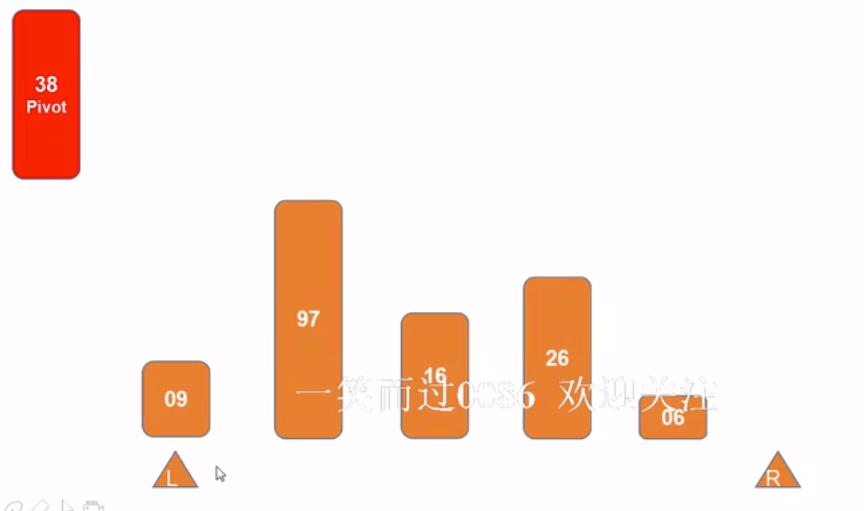
• 3）L右移，又开始比较，比pivot大，赋值给R的位置
  
  
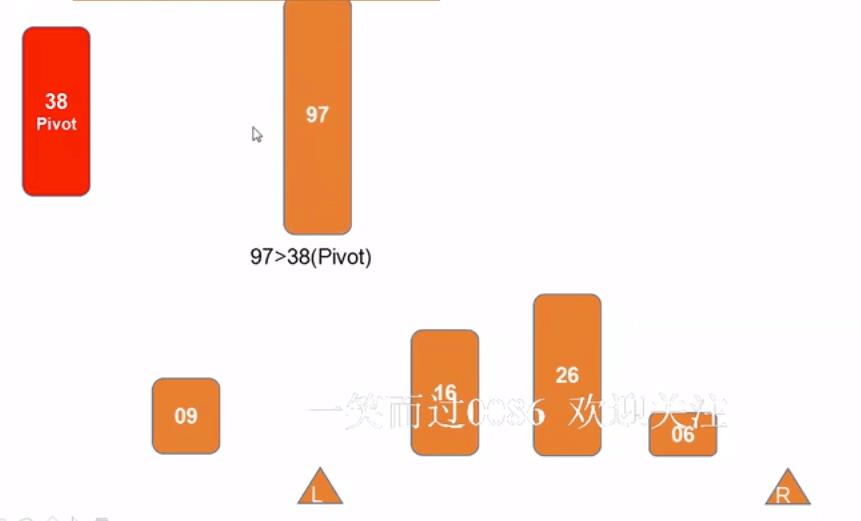
• 4）R开始左移，进行比较，比pivo小，赋值给L所在位置
  
  
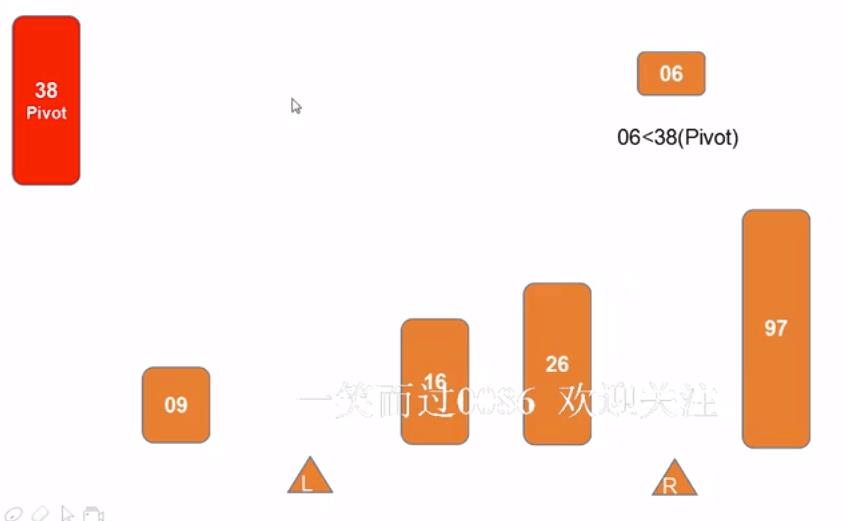
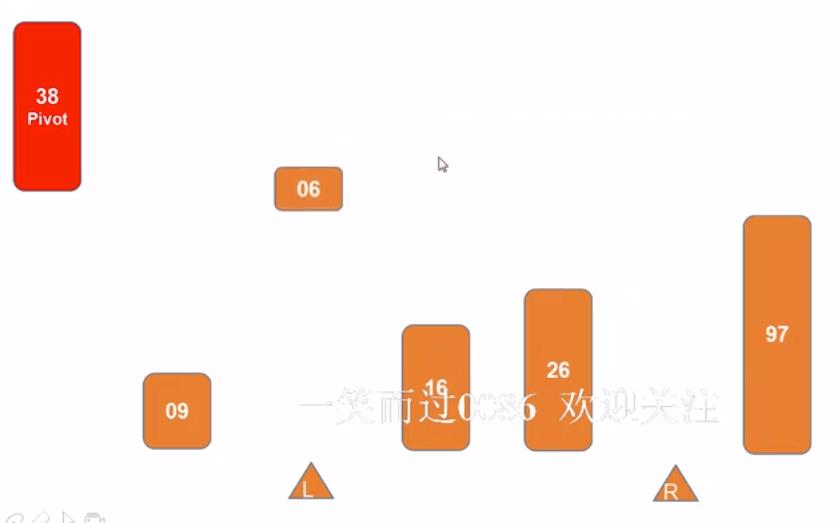
• 5）当L和R重合的时候，即pivot的位置确定，就是第一次排序结束，分出来两个子序列，右子序列只剩一个元素说明排序完成，左子序列继续重复以上步骤继续排序，直到所有子序列都只剩一个元素说明排序完成
  
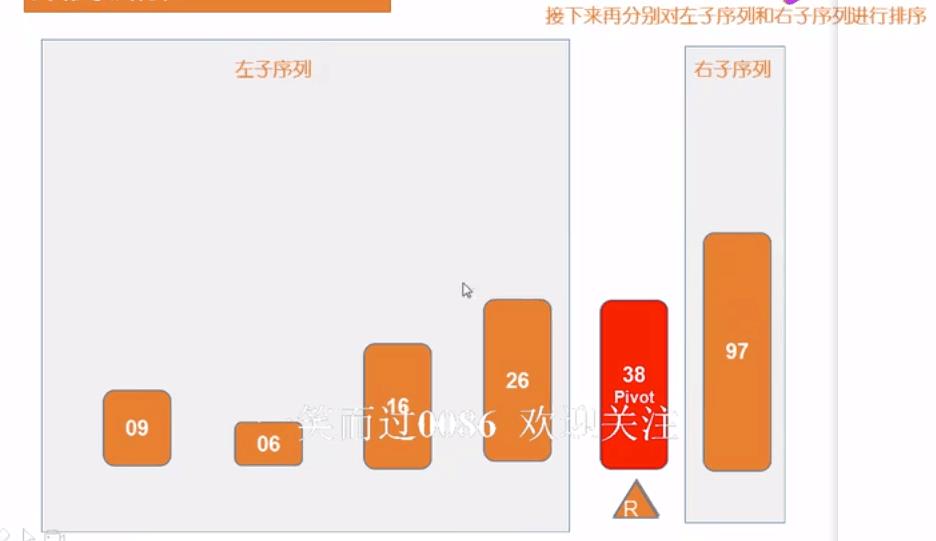
• 6）左子序列继续重复以上步骤排序（递归调用）
  
  
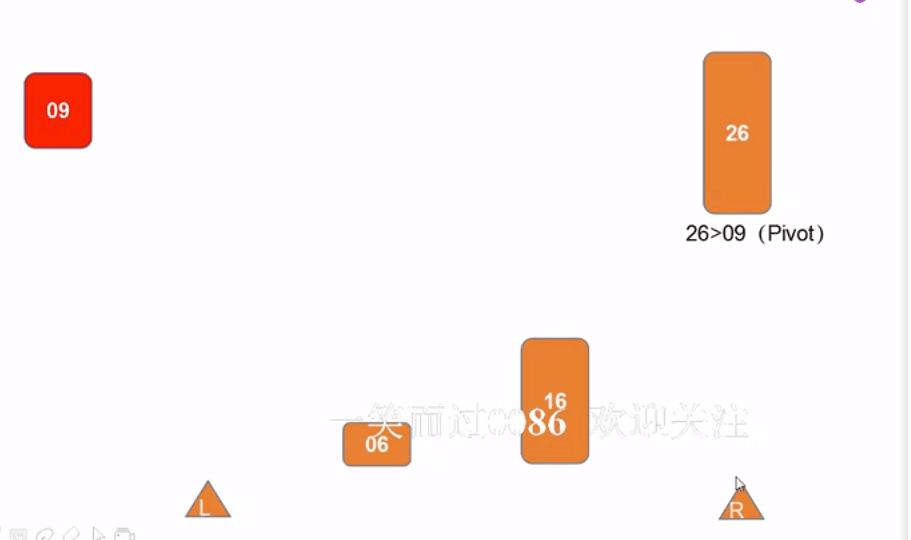
• 7）直到又只剩一个元素
  
• 8）重复直达每个子序列都只剩一个说明排序完成
  
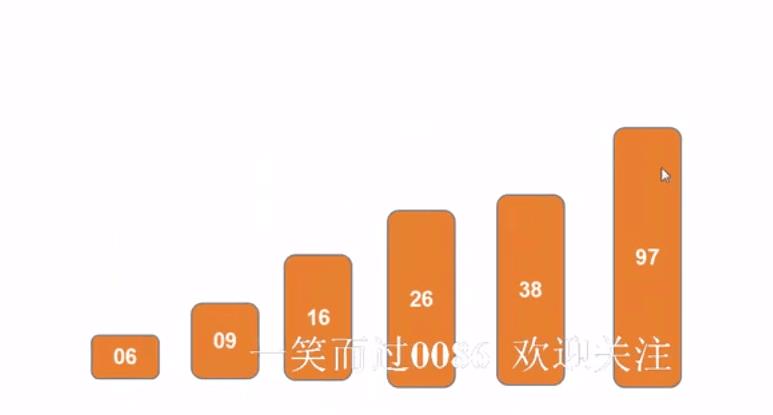
  这样应该就能感受到快排的精妙指出了吧，通过递归来实现分治思想无线细化，下面就用代码来展示一下！

1. 代码展示

#include <iostream>
using namespace std;

#define BUF_SIZE 8


void print(int arr[], int len)  //打印函数

    for (int i = 0; i < len; i++)
    
        cout << arr[i] << "  ";
    

    cout << endl;


void QuickSort(int arr[], int low, int high)

    if (low < high)
    
        int i = low;
        int j = high;
        int pivot = arr[low];

        while (i < j)
        
            while (i < j && arr[j] >= pivot) //找到比pivot小的数；
            
                j--; //high左移，继续寻找比pivot小的数
            
            if (i < j)
            
                arr[i++] = arr[j];  //找到比pivot小的数，将值赋值给左边，并让low右移
            

            while (i < j && arr[i] < pivot) //找到比pivot大的数；
            
                i++;  //low右移，继续寻找比pivot大的数
            
            if (i < j)
            
                arr[j--] = arr[i];  //找到比pivot大的数，将值赋值给右边，并让high左移
            
        

        arr[i] = pivot; //相遇后，将支点的值赋予此；

        QuickSort(arr, low, i - 1);     //左子序继续递归调用排序，i将序列分为两半，左边最大肯定是i-1个数；
        QuickSort(arr, i + 1, high);    //右子序继续递归调用排序，i将序列分为两半，右边最小肯定是i+1个数；
    



int main()

    int arr[BUF_SIZE] =  0 ;

    cout << "请任意输入8个整型数字：" << endl;

    for (int i = 0; i < BUF_SIZE; i++)
    
        cin >> arr[i];
    

    cout << "在使用快速排序前数组顺序：" << endl;

    print(arr, BUF_SIZE);

    QuickSort(arr, 0, BUF_SIZE - 1);

    cout << "排序后，数组的顺序是" << endl;

    print(arr, BUF_SIZE);

    return 0;

打印结果：

2. 代码优化

优化递归操作
什么是尾递归呢？如果一个函数中递归形式的调用出现是在函数末尾，我们称这个递归函数是尾递归的。
当编译器检测到一个函数使用尾递归的时候，他就覆盖当前的活跃记录，而不是在栈中去创建一个新的。编译器可以做到这一点，因为递归调用是当前活跃期内最后一条待执行的语句，于是当这个调用返回的时候栈帧中并没有其他事可做，因此也就没有保存栈帧的必要了。通过覆盖当前的栈帧而不是在之上重新添加一个，这样所使用的栈空间就大大缩减了，这使得运行效率会变得更高。
因此，只要有可能我们就需要将递归函数写成尾递归的形式。

3.时空分析

• 时间复杂度：O(nlog₂n)
• 空间复杂度：O(log₂n)
• 不稳定排序
  下篇博客介绍三种插入排序：点击 直接插入排序、折半插入排序、希尔排序