算法中数学相关知识-倍数约数完全数质数最小公倍数

Posted 2022-12-08 Jocelin47

1、倍数

大数除以小数,能整除没有余数,那么,大数就是小数的倍数,小数就是大数的因数

#include <iostream>

using namespace std;

int main()

    int a, b;
    cin >> a >> b;

    if (a % b == 0 || b % a == 0) 
        cout << "是倍数" << endl;
    else 
        cout << "不是倍数" << endl;

    return 0;

2、约数

2.1 输出一个数的所有约数

一个数的所有约数

#include <iostream>

using namespace std;

int main()

    int n;
    cin >> n;
    for (int i = 1; i <= n; i ++ )
        if (n % i == 0)
            cout << i << endl;

    return 0;

2.2 如何求一个数的所有约数个数

根据算数基本定理，N = P1 ^a1 * P2 ^a2 * … Pk ^ak （P1,P2…Pk都是质数）（求每个数的最小质因子，以及将N分解程上述形式得到每个Pk以及出现的次数ak保存到数组）

N的约数个数为（a1 + 1）（a2 + 1） …*（ak + 1）

2.3 约数之和公式

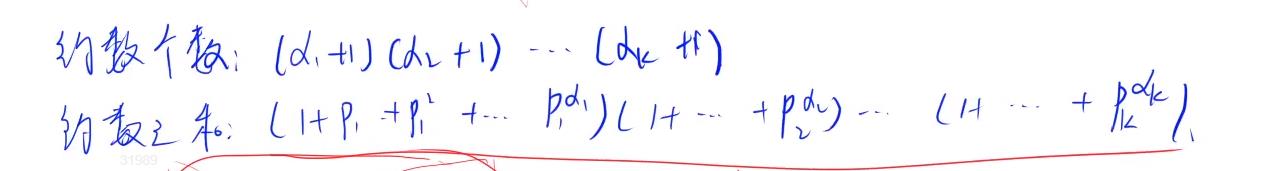
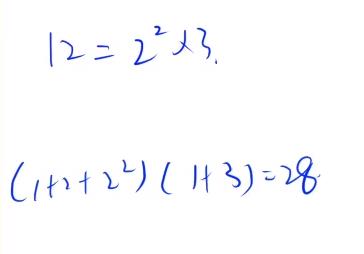
3、完全数

一个整数，除了本身以外的其他所有约数的和如果等于该数，那么我们就称这个整数为完全数。
进行优化，
i < num / i;
前一个约数小于后一个约数，避免整个遍历循环到num-1

#include<iostream>


using namespace std;


bool isPerfect(int num)

    if(num==0)
        return true;
    int res = 0;
    for(int i = 1;i*i <=num;i++) // i < num / i; 前一个约数小于后一个约数就可以了
    
        if(num%i==0)
        
            if( i < num) //约数小于
                res += i ;
            if( num/i < num ) //上面约数对应的另一个约数
                res +=num/i;
        
    
    if( res == num)
        return true;
    else
        return false;


int main()

    int n;
    cin >> n;
    while(n--)
    
        int num;
        cin >> num;
        if(isPerfect(num))
            printf("%d is perfect\\n",num);
        else
            printf("%d is not perfect\\n",num);
    
    return 0;

4、质数

4.1 普通求质数

一个大于1的自然数，如果除了1和它自身外，不能被其他自然数整除则称该数为质数。

#include<iostream>


using namespace std;

int n;

bool isPrime(int num)

    
    for(int i =2; i*i<=num;i++)
    
        if( num % i==0 || i%num==0 ) //判断从2开始到 i < num /i  当前数是否是num倍数，跟完美数一样的思路
            return false;
    
    return true;



int main()

    cin >> n;
    while(n--)
    
        int num;
        scanf("%d",&num);
        
        if(isPrime(num))
            printf("%d is prime\\n",num);
        else
            printf("%d is not prime\\n",num);
        
    
    return 0;

4.2 筛法求质数

const int N = 1000010;
int prime[N],cnt;//prime存我们的质数，cnt是质数的个数、
bool st[N]; //当前有没有被筛过
int minp[N];//存下每个数的最小质因子
int get_primes(int n) // O(n)

	for(int i =0; i <=n ;i++)
	
		if(st[i] == 0)  minp[i] = i,prime[cnt++] = i;
		//从小到大把i倍的质数筛掉,筛掉的一定是合数，且用其最小值因子筛的
		for(int j =0; i * prime[j]  <= n; j++)
		
			st[ i * prime[j] ] = true;
			minp[ i * prime[j] ] = prime[j]; //合数的最小质因子
			//如果prime[j]为i的最小质因子就break;
			if( i % prime[j] == 0)
				break;
		
	

5、最小公倍数

a,b最小公倍数= a*b /gcd(a,b);

#include<iostream>


using namespace std;

int gcd(int a,int b)

    if( b > a)
        return gcd(b,a);
    return b==0?a:gcd(b,a%b);


int lcm(int a, int b)

    return a*b / gcd(a,b);



int main()

    int a,b;
    cin >> a >> b;
    cout << lcm(a,b);
    return 0;