理论： 数论：素数基础

Posted 2022-12-07 sun897949163

素数定义

正整数1只有一个正整数因子， 任意其他的正整数至少有两个正整数因子， 因为它一定可以被1和他本身整除。只有两个正因子的整数称之为素数。

素数的性质

定义2.1： 素数是大于1的正整数， 并且除了1和他本身之外不崩被其他正整数整除， 大于1的非素数称之为合数

素数具有以下的性质：
（1）.a>1是合数， 当且仅当a = bc， 其中 1 < b < a, 1 < c < a;
（2）.合数必有素数因子
（3）.如果d>1 ， p是素数， 且d|p, 则 d= p；
（4）.设p是素数且(p | ab)， 则必有（p|a）或者（p|b）
素数的特性
（1）.存在无穷多个素数。
（2）.每个大于一的正整数都有一个素因子

素数分布

素数有无穷多个， 能估计出小于一个正实数X的素数有多少个并用π（x）来表示，这就是素数定理

定理2.1：
.

注：次公式的极限沿负向趋近于1

推论：令PN是第n个素数， 其中n是正整数， 那么pn~n·ln(n)
定理2.2： 对于任意正整数n, 存在至少n个连续 的正合数

素数猜想

1.勃兰特猜想：

对于给定的正整数n，其中n> 1， 存在一个素数p， 使得n < p < 2n.

2.孪生素数猜想

存在无穷多个形如p, p+2 的素数对

3.哥德巴赫猜想

任何大于2的正偶数可以写成两个素数的和

4.n^2+1猜想

存在无穷多个形如n^2 + 1的素数。

素数测试

素数基本判别法： 如果正整数n是素数， 当且仅当他不能被任何一个小于sqrt（n）的数整除
·

埃拉托色尼筛法

定理2.3： 如果n是一个合数， 那么n一定有一个不超过sqrt（n）的素数因子
推论：如果n是一个合数， 则n必有小于等于sqrt（n）的素数因子

6N+1法

对于任何一个自然数， 总可以表示为如下的形式：
6N, 6N+1, 6N+2, 6N+3, 6N+4, 6N+5;

其中 6N+2, 6N+3, 6N+4, 都不是素数， 只有形如6N+1和6N+5的才有可能数素数， 所以除了2和3之外， 所有的素数都能表示成为6N±1的形式（N为自然数）

有关素数的基本定理

定理2.4： 每个大于1的正整数n，都能以被唯一的写成素数的乘积， 在成绩中的素数因子按照非降序排列。正整数n的分解式
.

**

上式称之为n的标准分解式， 其中

.

由上式我们可以推导出如下的性质：

（1）.

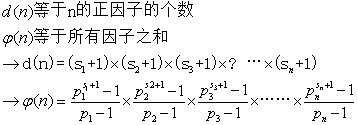
那个问号蜜汁乱入

（2）.

（3）.n!的素数分解中的素数p的幂为
.

梅森素数及其判定

定义2.2： 如果m是一个正整数， 且2^m-1是一个素数， 则m必定是素数， 反之如果m是素数， 则Mm=2^m-1称之为第m个梅森数。

梅森数可能是素数也可能是合数

判定方法

卢卡斯-莱默素性测试是非常简单的：如果 P > 2， 2^P-1 是素数当且仅当 S(p-2) = 0，其中，S0 = 4，Sn = (S(n-1)^2 - 2) mod (2^p-1)。例如，证明 27 - 1 是素数的过程如下：

S0 = 4
S1 = (4 * 4 - 2) mod 127 = 14
S2 = (14 * 14 - 2) mod 127 = 67
S3 = (67 * 67 - 2) mod 127 = 42
S4 = (42 * 42 - 2) mod 127 = 111
S5 = (111 * 111 - 2) mod 127 = 0

//判断梅森数Ｍｐ是不是梅森素数
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

long long multi(long long a, long long b, long long m) //a * b % m

    long long ret = 0;
    while(b > 0)
    
        if(b & 1)
            ret = (ret + a) % m;
        b = b >> 1;
        a = (a << 1) % m;
    
    return ret;


int main (void)

    long long sum = 1, date[66], temp;
    int n, p;
    date[1] = 4;
    scanf("%d", &n);
    while(n--)
    
        sum = 1;
        scanf("%d", &p);
        sum  = (1 << p) - 1;
        for(int i = 2; i <= p - 1; i++)
        
            temp = multi(date[i - 1], date[i - 1], sum);
            date[i] = (temp - 2) % sum;
        
        if(p == 2)
            printf("yes\\n");
        else
        
            if(date[p - 1] == 0)
                printf("yes\\n");
            else
                printf("no\\n");
        
    
    return 0;

Miller素数测试法：
随机算法 不会证明， 具体可以看这里， 还有这里

#include<time.h>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define time 12

using namespace std;

long long random(long long n)

    return (long long)((double) rand() / RAND_MAX * n + 0.5);


long long multi(long long a, long long b, long long m) // a * b % m

    long long ret = 0;
    while (b > 0)//将乘法转化为加法
    
        if(b & 1)
            ret = (ret + a) % m;
        b = b >> 1;
        a = (a << 1) % m;
    
    return ret;


long long quick_mod(long long a, long long b, long long m)// a ^ b % m

    long long ans = 1;
    a %= m;
    while(b)
    
        if(b & 1)
        
            ans = multi(ans, a, m);
            b--;
        
        b /= 2;
        a = multi(a, a, m);
    
    return ans;


bool witness(long long a, long long n)

    long long m = n - 1;
    int j = 0;
    while(!(m & 1))
    
        j++;
        m = m >> 1;
    
    long long x = quick_mod(a, m, n);
    if(x == 1 || x == n - 1)
    
        return false;
    
    while(j--)
    
        x = x * x % n;
        if(x == n - 1)
            return false;
    
    return true;



bool miller_rabin(long long n)

    if (n < 2)
        return false;
    if (n == 2)
        return true;
    if (!(n & 1))
        return false;
    for (int i = 1; i <= time; i++)
    
        long long a = random(n - 2) + 1;
        if(witness(a, n))
            return false;
    
    return true;


int main (void)

    int ncase, p;
    long long n;
    scanf("%d", &ncase);
    while(ncase--)
    
        scanf("%d", &p);
        n = ((long long ) 1 << p) - 1;
        if(miller_rabin(n))
            printf("yes\\n");
        else
            printf("no\\n");
    
    return 0;