dijkstra算法学习

Posted 2020-11-19 nathan2young

dijkstra算法学习

一、最短路径

单源最短路径：计算源点到其他各顶点的最短路径的长度

全局最短路径：图中任意两点的最短路径

Dijkstra、Bellman-Ford、SPFA求单源最短路径

Floyed可以求全局最短路径，但是效率比较低

SPFA算法是Bellman-Ford算法的队列优化

Dijkstra算法不能求带负权边的最短路径，而SPFA算法、Bellman-Ford算法、Floyd-Warshall可以求带负权边的最短路径。

Bellman-Ford算法的核心代码只有4行，Floyd-Warshall算法的核心代码只有5行。

深度优先遍历可以求一个点到另一个点的最短路径的长度

二、dijkstra算法图解

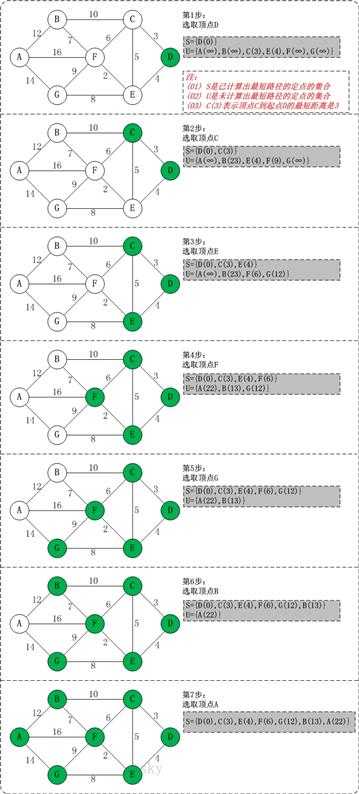
三、算法步骤

1.初始化，选择好初始点，设总共有vexnum个节点，则总共要将vexnum-1个节点放入s中

for(i = 1;i<G.vexnum;i++)

2.遍历U，找出其中最短路径的点，并作记录（放入S中）

    // 遍历G.vexnum-1次；每次找出一个顶点的最短路径。
    for (i = 1; i < G.vexnum; i++)
    {
        // 寻找当前最小的路径；
        // 即，在未获取最短路径的顶点中，找到离vs最近的顶点(k)。
        min = INF;
        for (j = 0; j < G.vexnum; j++)
        {
            if (flag[j]==0 && dist[j]<min)
            {
                min = dist[j];
                k = j;
            }
        }
        // 标记"顶点k"为已经获取到最短路径
        flag[k] = 1;

3.更新剩余U中节点的距离：设步骤2中加入的节点为k，最短距离为min，则if（k的邻居到k的距离+min）<dist(D,k的邻居)，则更新dist（D，k的邻居）

        // 修正当前最短路径和前驱顶点
        // 即，当已经"顶点k的最短路径"之后，更新"未获取最短路径的顶点的最短路径和前驱顶点"。
        for (j = 0; j < G.vexnum; j++)
        {
            tmp = (G.matrix[k][j]==INF ? INF : (min + G.matrix[k][j])); // 防止溢出
            if (flag[j] == 0 && (tmp  < dist[j]) )
            {
                dist[j] = tmp;
                prev[j] = k;
            }
        }
    }

四、完整代码

/*
 * Dijkstra最短路径。
 * 即，统计图(G)中"顶点vs"到其它各个顶点的最短路径。
 *
 * 参数说明：
 *        G -- 图
 *       vs -- 起始顶点(start vertex)。即计算"顶点vs"到其它顶点的最短路径。
 *     prev -- 前驱顶点数组。即，prev[i]的值是"顶点vs"到"顶点i"的最短路径所经历的全部顶点中，位于"顶点i"之前的那个顶点。
 *     dist -- 长度数组。即，dist[i]是"顶点vs"到"顶点i"的最短路径的长度。
 */
void dijkstra(Graph G, int vs, int prev[], int dist[])
{
    int i,j,k;
    int min;
    int tmp;
    int flag[MAX];      // flag[i]=1表示"顶点vs"到"顶点i"的最短路径已成功获取。

    // 初始化
    for (i = 0; i < G.vexnum; i++)
    {
        flag[i] = 0;              // 顶点i的最短路径还没获取到。
        prev[i] = 0;              // 顶点i的前驱顶点为0。
        dist[i] = G.matrix[vs][i];// 顶点i的最短路径为"顶点vs"到"顶点i"的权。
    }

    // 对"顶点vs"自身进行初始化
    flag[vs] = 1;
    dist[vs] = 0;

    // 遍历G.vexnum-1次；每次找出一个顶点的最短路径。
    for (i = 1; i < G.vexnum; i++)
    {
        // 寻找当前最小的路径；
        // 即，在未获取最短路径的顶点中，找到离vs最近的顶点(k)。
        min = INF;
        for (j = 0; j < G.vexnum; j++)
        {
            if (flag[j]==0 && dist[j]<min)
            {
                min = dist[j];
                k = j;
            }
        }
        // 标记"顶点k"为已经获取到最短路径
        flag[k] = 1;

        // 修正当前最短路径和前驱顶点
        // 即，当已经"顶点k的最短路径"之后，更新"未获取最短路径的顶点的最短路径和前驱顶点"。
        for (j = 0; j < G.vexnum; j++)
        {
            tmp = (G.matrix[k][j]==INF ? INF : (min + G.matrix[k][j])); // 防止溢出
            if (flag[j] == 0 && (tmp  < dist[j]) )
            {
                dist[j] = tmp;
                prev[j] = k;
            }
        }
    }

    // 打印dijkstra最短路径的结果
    printf("dijkstra(%c): 
", G.vexs[vs]);
    for (i = 0; i < G.vexnum; i++)
        printf("  shortest(%c, %c)=%d
", G.vexs[vs], G.vexs[i], dist[i]);
}

参考资料：http://www.cnblogs.com/skywang12345/p/3711512.html