2014ACM/ICPC亚洲区鞍山赛区现场赛题解报告
Posted queuelovestack
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了2014ACM/ICPC亚洲区鞍山赛区现场赛题解报告相关的知识，希望对你有一定的参考价值。
此文章可以使用目录功能哟↑(点击上方[+])
练习了一下前年鞍山赛区的区域赛题,感觉整个人状态都不对,各种低级错误频出,诸如数组开小了,中间结果爆int了等等,看来还是得多练...
链接→2014ACM/ICPC亚洲区鞍山赛区现场赛——题目重现
Problem 1002 Chat
Accept: 0 Submit: 0
Time Limit: 2000/1000 MS (Java/Others) Memory Limit : 262144/262144 K (Java/Others)
Problem Description
As everyone knows, DRD has no girlfriends. But as everyone also knows, DRD’s friend ATM’s friend CLJ has many potential girlfriends. One evidence is CLJ’s chatting record.
CLJ chats with many girls all the time. Sometimes he begins a new conversation and sometimes he ends a conversation. Sometimes he chats with the girl whose window is on the top.
You can imagine CLJ’s windows as a queue. The first girl in the queue is the top girl if no one is “always on top ”.
Since CLJ is so popular, he begins to assign a unique positive integer as priority for every girl. The higher priority a girl has, the more CLJ likes her. For example, GYZ has priority 109, and JZP has priority 108 while Sister Soup has priority 1, and Face Face has priority 2.
As a famous programmer, CLJ leads a group to implement his own WM(window manager). The WM will log CLJ’s operations. Now you are supposed to implement the log system. The general logging format is “Operation #X: LOGMSG.”, where X is the number of the operation and LOGMSG is the logging message.
There are several kinds of operations CLJ may use:
1.Add u: CLJ opens a new window whose priority is u, and the new window will be the last window in the window queue. This operation will always be successful except the only case in which there is already a window with priority u. If it is successful, LOGMSG will be “success”. Otherwise LOGMSG will be “same priority”.
2.Close u: CLJ closes a window whose priority is u. If there exists such a window, the operation will be successful and LOGMSG will be “close u with c”, where u is the priority and c is the number of words CLJ has spoken to this window. Otherwise, LOGMSG will be “invalid priority”. Note that ANY window can be closed.
3.Chat w: CLJ chats with the top window, and he speaks w words. The top window is the first window in the queue, or the “always on top” window (as described below) instead if there exists. If no window is in the queue, LOGMSG will be “empty”, otherwise the operation can be successful and LOGMSG will be “success”.
4.Rotate x: CLJ performs one or more Alt-Tabs to move the x-th window to the first one in the queue. For example, if there are 4 windows in the queue, whose priorities are 1, 3, 5, 7 respectively and CLJ performs “Rotate 3”, then the window’s priorities in the queue will become 5, 1, 3, 7. Note that if CLJ wants to move the first window to the head, this operation is still considered “successful”. If x is out of range (smaller than 1 or larger than the size of the queue), LOGMSG will be “out of range”. Otherwise LOGMSG should be “success”.
5.Prior: CLJ finds out the girl with the maximum priority and then moves the window to the head of the queue. Note that if the girl with the maximum priority is already the first window, this operation is considered successful as well. If the window queue is empty, this operation will fail and LOGMSG must be “empty”. If it is successful, LOGMSG must be “success”.
6.Choose u: CLJ chooses the girl with priority u and moves the window to the head of the queue.This operation is considered successful if and only if the window with priority u exists. LOGMSG for the successful cases should be “success” and for the other cases should be “invalid priority”.
7.Top u: CLJ makes the window of the girl with priority u always on top. Always on top is a special state, which means whoever the first girl in the queue is, the top one must be u if u is always on top. As you can see, two girls cannot be always on top at the same time, so if one girl is always on top while CLJ wants another always on top, the first will be not always on top any more, except the two girls are the same one. Anyone can be always on top. LOGMSG is the same as that of the Choose operation.
8.Untop: CLJ cancels the “always on top” state of the girl who is always on top. That is, the girl who is always on top now is not in this special state any more. This operation will fail unless there is one girl always on top. If it fails, LOGMSG should be “no such person”, otherwise should be “success”.
As a gentleman, CLJ will say goodbye to every active window he has ever spoken to at last, “active” here means the window has not been closed so far. The logging format is “Bye u: c” where u is the priority and c is the number of words he has ever spoken to this window. He will always say good bye to the current top girl if he has spoken to her before he closes it.
Input
The first line contains an integer T (T ≤ 10), denoting the number of the test cases.
For each test case, the first line contains an integer n(0 < n ≤ 5000), representing the number of operations. Then follow n operations, one in a line. All the parameters are positive integers below 10^9.
Output
Output all the logging contents.
Sample Input
1
18
Prior
Add 1
Chat 1
Add 2
Chat 2
Top 2
Chat 3
Untop
Chat 4
Choose 2
Chat 5
Rotate 2
Chat 4
Close 2
Add 3
Prior
Chat 2
Close 1
Sample Output
Operation #1: empty.
Operation #2: success.
Operation #3: success.
Operation #4: success.
Operation #5: success.
Operation #6: success.
Operation #7: success.
Operation #8: success.
Operation #9: success.
Operation #10: success.
Operation #11: success.
Operation #12: success.
Operation #13: success.
Operation #14: close 2 with 8.
Operation #15: success.
Operation #16: success.
Operation #17: success.
Operation #18: close 1 with 11.
Bye 3: 2
Hint
This problem description does not relate to any real person in THU.
Problem Idea
解题思路:
【题意】
对窗口队列进行8种操作(对应的要输出反馈信息):
①Add u:往窗口队列末尾加入一个优先级为u的窗口,若窗口队列中已经存在优先级为u的窗口,反馈信息为"same priority",且不进行该操作;否则,反馈信息为"success"
②Close u:将窗口队列中优先级为u的窗口关闭,若窗口队列中不存在优先级为u的窗口,反馈信息为"invalid priority",且不进行该项操作;否则,反馈信息为"close u with c",其中,u表示关闭窗口的优先级,c表示CLJ在该窗口说的词数(word)
③Chat w:CLJ在top window内说了w个词(word),top window = “always on top” window(优先)/the first window in the queue,即若存在"置顶窗口",则top window为置顶窗口,否则为窗口队列中的第一个窗口,当窗口队列为空时,不进行该操作,且反馈信息为"empty";否则反馈信息为"success"
④Rotate x:将窗口队列中的第x个窗口移动到窗口队列的最前面,当x小于1或大于窗口队列中的窗口数时,反馈信息为"out of range",且不进行该操作;否则反馈信息为"success"
⑤Prior:将窗口队列中优先级最高的窗口移动到窗口队列的最前面,显然,当窗口队列为空时,该操作无效,反馈信息为"empty";否则反馈信息为"success"
⑥Choose u:将窗口队列中优先级为u的窗口移动到窗口队列的最前面,当窗口队列中不存在优先级为u的窗口时,该操作无效,反馈信息为"invalid priority";否则反馈信息为"success"
⑦Top u:将窗口队列中优先级为u的窗口标记为"置顶"窗口,但在窗口队列中的位置不变,当窗口队列中不存在优先级为u的窗口时,该操作无效,反馈信息为"invalid priority";否则反馈信息为"success"
⑧Untop:取消"置顶"窗口的"置顶"状态,若当前没有窗口被"置顶",则该操作无效,反馈信息为"no such person";否则反馈信息为"success"
最终,CLJ要跟那些说过话的且还未被关闭的窗口say goodbye,若存在"置顶"窗口,优先say goodbye,其余按照窗口队列顺序即可
【类型】
巨型模拟题(巨型,只是因为太麻烦,操作超级多)
【分析】
此题用什么方法都好,只要细节考虑清楚就可以,毕竟人家本来就没有打算在时限上卡你
需注意的细节有:
⑴say goodbye要先对 always on top 的人说
⑵对没有说过话的不要说 goodbye
⑶一个窗口中说过的词数可能会爆int
⑷always on top只是一种状态,它不会改变一个窗口在窗口队列中的位置
⑸关闭窗口时,若关闭的是"always on top"窗口,要记得将"是否存在置顶窗口"的标记清空
暂时就这么几点,欢迎补充
【时间复杂度&&优化】
O(n^2)
题目链接→HDU 5071 Chat
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<list>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 5005;
const int M = 100005;
const int inf = 1000000007;
const int mod = 1000000007;
map<int,int> m;
list<int> l;
int p,top;
__int64 ans[N];
void Add(int u)
if(m[u])
puts("same priority.");
return ;
puts("success.");
m[u]=p++;
l.push_back(u);
void Close(int u)
if(!m[u])
puts("invalid priority.");
return ;
printf("close %d with %I64d.\\n",u,ans[m[u]]);
m[u]=0;
l.remove(u);
if(top==u)
top=0;
void Chat(int w)
if(l.empty())
puts("empty.");
return ;
puts("success.");
if(top)
ans[m[top]]+=w;
else
ans[m[l.front()]]+=w;
void Rotate(int x)
if(x<1||x>l.size())
puts("out of range.");
return ;
puts("success.");
list<int>::iterator it;
int i;
for(i=1,it=l.begin();it!=l.end()&&i<x;it++,i++);
//printf("%d\\n",*it);
int tmp=*it;
l.erase(it);
l.push_front(tmp);
void Prior()
if(l.empty())
puts("empty.");
return ;
int i,x,Max=0;
list<int>::iterator it;
for(i=1,it=l.begin();it!=l.end();it++,i++)
if(*it>Max)
Max=*it,x=i;
Rotate(x);
void Choose(int u)
if(!m[u])
puts("invalid priority.");
return ;
int x;
list<int>::iterator it;
for(x=1,it=l.begin();it!=l.end();it++,x++)
if(*it==u)
break;
Rotate(x);
void Top(int u)
if(!m[u])
puts("invalid priority.");
return ;
puts("success.");
top=u;
void Untop()
if(!top)
puts("no such person.");
return ;
puts("success.");
top=0;
char s[10];
int main()
int t,n,i,u,w,x;
scanf("%d",&t);
while(t--)
p=1;top=0;
m.clear();
l.clear();
memset(ans,0,sizeof(ans));
scanf("%d",&n);
for(i=1;i<=n;i++)
printf("Operation #%d: ",i);
scanf("%s",s);
if(!strcmp(s,"Add"))
scanf("%d",&u);
Add(u);
else if(!strcmp(s,"Close"))
scanf("%d",&u);
Close(u);
else if(!strcmp(s,"Chat"))
scanf("%d",&w);
Chat(w);
else if(!strcmp(s,"Rotate"))
scanf("%d",&x);
Rotate(x);
else if(!strcmp(s,"Prior"))
Prior();
else if(!strcmp(s,"Choose"))
scanf("%d",&u);
Choose(u);
else if(!strcmp(s,"Top"))
scanf("%d",&u);
Top(u);
else if(!strcmp(s,"Untop"))
Untop();
if(top&&ans[m[top]])
printf("Bye %d: %I64d\\n",top,ans[m[top]]);
list<int>::iterator it;
for(it=l.begin();it!=l.end();it++)
if(*it!=top&&ans[m[*it]])
printf("Bye %d: %I64d\\n",*it,ans[m[*it]]);
return 0;
Problem 1004 Galaxy
Accept: 0 Submit: 0
Time Limit: 2000/1000 MS (Java/Others) Memory Limit : 262144/262144 K (Java/Others)
Special Judge
Problem Description
Good news for us: to release the financial pressure, the government started selling galaxies and we can buy them from now on! The first one who bought a galaxy was Tianming Yun and he gave it to Xin Cheng as a present.
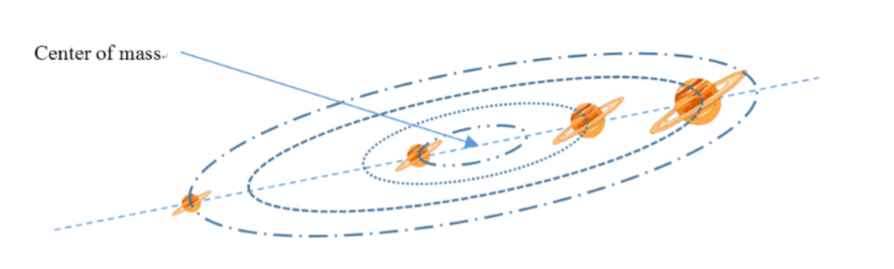
To be fashionable, DRD also bought himself a galaxy. He named it Rho Galaxy. There are n stars in Rho Galaxy, and they have the same weight, namely one unit weight, and a negligible volume. They initially lie in a line rotating around their center of mass.
Everything runs well except one thing. DRD thinks that the galaxy rotates too slow. As we know, to increase the angular speed with the same angular momentum, we have to decrease the moment of inertia.
The moment of inertia I of a set of n stars can be calculated with the formula
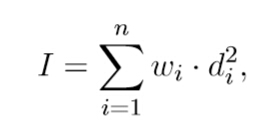
where wi is the weight of star i, di is the distance form star i to the mass of center.
As DRD’s friend, ATM, who bought M78 Galaxy, wants to help him. ATM creates some black holes and white holes so that he can transport stars in a negligible time. After transportation, the n stars will also rotate around their new center of mass. Due to financial pressure, ATM can only transport at most k stars. Since volumes of the stars are negligible, two or more stars can be transported to the same position.
Now, you are supposed to calculate the minimum moment of inertia after transportation.
Input
The first line contains an integer T (T ≤ 10), denoting the number of the test cases.
For each test case, the first line contains two integers, n(1 ≤ n ≤ 50000) and k(0 ≤ k ≤ n), as mentioned above. The next line contains n integers representing the positions of the stars. The absolute values of positions will be no more than 50000.
Output
For each test case, output one real number in one line representing the minimum moment of inertia. Your answer will be considered correct if and only if its absolute or relative error is less than 1e-9.
Sample Input
2
3 2
-1 0 1
4 2
-2 -1 1 2
Sample Output
0
0.5
Problem Idea
解题思路:
【题意】
有n个质量相同(1个单位重量),体积可以忽略的星球(质点),最初在一条直线上,围绕n个点的质心旋转
为了使得惯性矩尽可能小,现在可移动k个星球的位置
问最小的惯性矩I为多少
【类型】
贪心+公式推导->暴力
【分析】
由于每个星球的质量都是1个单位重量,故上述公式中的wi=1
di表示的是每个星球和质心的距离,我们现在知道每个星球的位置,但质心位置还不知道
由n个点的质心计算公式可得质心位置
化简后的惯性矩计算公式
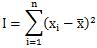
有没有觉得很熟悉╮(╯_╰)╭
跟方差计算公式很像,而方差表示的是点的离散程度,所以要使惯性矩尽可能小,我们必然也需要选取尽可能接近的点
即必定是直线上连续的点
此外,要移动的k个点必然是移动到质心位置,只有这样这k个点对惯性矩的贡献为0
于是,此题就转化成从n个点中选取n-k个点,使得它们的方差*n尽可能小
所以我们将最初的n个点从小到大排序之后,每n-k个点求一次惯性矩,取最小的即可
但是考虑到每n-k个点求一次惯性矩的时间复杂度还是有点大,所以我们要进行一次优化
即必须找到
的惯性矩与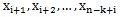
的惯性矩的关系
于是将惯性矩公式继续化简
这样相邻两次惯性矩的计算就有了关联
而我们只需预处理出
和
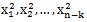即可
特判n==k的情况,这种没有多余星球剩下,故输出0即可
【时间复杂度&&优化】
O(nlogn)
题目链接→HDU 5073 Galaxy
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 50005;
const int M = 100005;
const int inf = 1000000007;
const int mod = 1000000007;
__int64 s[N];
int main()
int t,n,k,i,j;
__int64 f,h;
double ans;
scanf("%d",&t);
while(t--)
f=h=0;
scanf("%d%d",&n,&k);
for(i=1;i<=n;i++)
scanf("%I64d",&s[i]);
if(n==k)
puts("0.0000000000");
continue;
sort(s+1,s+n+1);
for(i=1;i<=n-k;i++)
f+=s[i]*s[i],h+=s[i];
for(j=1,ans=1.0*f-1.0*h*h/(n-k);i<=n;i++,j++)
f=f-s[j]*s[j]+s[i]*s[i];
h=h-s[j]+s[i];
ans=min(ans,1.0*f-1.0*h*h/(n-k));
printf("%.10f\\n",ans);
return 0;
Problem 1005 Hatsune Miku
Accept: 0 Submit: 0
Time Limit: 2000/1000 MS (Java/Others) Memory Limit : 262144/262144 K (Java/Others)
Problem Description
Hatsune Miku is a popular virtual singer. It is very popular in both Japan and China. Basically it is a computer software that allows you to compose a song on your own using the vocal package.
Today you want to compose a song, which is just a sequence of notes. There are only m different notes provided in the package. And you want to make a song with n notes.
Also, you know that there is a system to evaluate the beautifulness of a song. For each two consecutive notes a and b, if b comes after a, then the beautifulness for these two notes is evaluated as score(a, b).
So the total beautifulness for a song consisting of notes a1, a2, . . . , an, is simply the sum of score(ai, ai+1) for 1 ≤ i ≤ n - 1.
Now, you find that at some positions, the notes have to be some specific ones, but at other positions you can decide what notes to use. You want to maximize your song’s beautifulness. What is the maximum beautifulness you can achieve?
Input
The first line contains an integer T (T ≤ 10), denoting the number of the test cases.
For each test case, the first line contains two integers n(1 ≤ n ≤ 100) and m(1 ≤ m ≤ 50) as mentioned above. Then m lines follow, each of them consisting of m space-separated integers, the j-th integer in the i-th line for score(i, j)( 0 ≤ score(i, j) ≤ 100). The next line contains n integers, a1, a2, . . . , an (-1 ≤ ai ≤ m, ai ≠ 0), where positive integers stand for the notes you cannot change, while negative integers are what you can replace with arbitrary notes. The notes are named from 1 to m.
Output
For each test case, output the answer in one line.
Sample Input
2
5 3
83 86 77
15 93 35
86 92 49
3 3 3 1 2
10 5
36 11 68 67 29
82 30 62 23 67
35 29 2 22 58
69 67 93 56 11
42 29 73 21 19
-1 -1 5 -1 4 -1 -1 -1 4 -1
Sample Output
270
625
Problem Idea
解题思路:
【题意】
有m种音符,对于任意两个连续音符a和b,假如b在a后,那么这两个音符的魅力值为score(a,b)
现有一个音符序列,已经知道某些位置的音符,要求补全整个音符序列后的魅力值最大
问魅力值为多少
【类型】
动态规划(DP)
【分析】
显然,此题局部最优并不能保证整体最优(例如我们已经知道某个位置的音符,但并不能确定它前一个音符一定是哪个,因为你虽然做到此处最优,但整体并不一定是最优的),故贪心是不可取的
所以我们从动态规划入手
令dp[i][j]表示对于第i个音符,以音符j结尾的音符序列的最大魅力值
那么转移方程为
①当位置i和位置i-1的音符s[i],s[i-1]已知时
这种情况下,因为音符已经固定,所以直接计算即可,dp[i][s[i]]=dp[i-1][s[i-1]]+score(s[i-1],s[i])
②当位置i的音符s[i]已知,位置i-1的音符s[i-1]未知时
s[i-1]可能是m种音符里的任意一种,故dp[i][s[i]]=maxdp[i-1][k]+score(k,s[i]),k∈[1,m]
③当位置i的音符s[i]未知,位置i-1的音符s[i-1]已知时
s[i]可能是m种音符里的任意一种,故dp[i][k]=maxdp[i-1][s[i-1]]+score(s[i-1],k),k∈[1,m]
④当位置i和位置i-1的音符s[i],s[i-1]未知时
s[i]和s[i-1]均可能是m种音符里的任意一种,能构成m*m种搭配,dp[i][k]=maxdp[i-1][j]+score(j,k),j,k∈[1,m]
最终只要挑出最大的dp[n][]即可
【时间复杂度&&优化】
O(N*M*M)
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 55;
const int M = 100005;
const int inf = 1000000007;
const int mod = 1000000007;
int s[N][N],a[2*N],dp[2*N][N];
int main()
int t,n,m,i,j,k,Max;
scanf("%d",&t);
while(t--)
memset(dp,0,sizeof(dp));
scanf("%d%d",&n,&m);
for(i=1;i<=m;i++)
for(j=1;j<=m;j++)
scanf("%d",&s[i][j]);
for(i=1;i<=n;i++)
scanf("%d",&a[i]);
for(i=2;i<=n;i++)
if(a[i]!=-1)
if(a[i-1]!=-1)
dp[i][a[i]]=dp[i-1][a[i-1]]+s[a[i-1]][a[i]];
else
for(j=1;j<=m;j++)
dp[i][a[i]]=max(dp[i][a[i]],dp[i-1][j]+s[j][a[i]]);
else
if(a[i-1]!=-1)
for(j=1;j<=m;j++)
dp[i][j]=max(dp[i][j],dp[i-1][a[i-1]]+s[a[i-1]][j]);
else
for(j=1;j<=m;j++)
for(k=1;k<=m;k++)
dp[i][k]=max(dp[i][k],dp[i-1][j]+s[j][k]);
/*Max=0;
for(j=1;j<=m;j++)
Max=max(Max,dp[i][j]);
printf("%d\\n",Max);*/
Max=0;
for(i=1;i<=m;i++)
Max=max(Max,dp[n][i]);
printf("%d\\n",Max);
return 0;
Problem 1009 Osu!
Accept: 0 Submit: 0
Time Limit: 2000/1000 MS (Java/Others) Memory Limit : 262144/262144 K (Java/Others)
Special Judge
Problem Description
Osu! is a very popular music game. Basically, it is a game about clicking. Some points will appear on the screen at some time, and you have to click them at a correct time.
Now, you want to write an algorithm to estimate how diffecult a game is.
To simplify the things, in a game consisting of N points, point i will occur at time ti at place (xi, yi), and you should click it exactly at ti at (xi, yi). That means you should move your cursor from point i to point i+1. This movement is called a jump, and the difficulty of a jump is just the distance between point i and point i+1 divided by the time between ti and ti+1. And the difficulty of a game is simply the difficulty of the most difficult jump in the game.
Now, given a description of a game, please calculate its difficulty.
Input
The first line contains an integer T (T ≤ 10), denoting the number of the test cases.
For each test case, the first line contains an integer N (2 ≤ N ≤ 1000) denoting the number of the points in the game. Then N lines follow, the i-th line consisting of 3 space-separated integers, ti(0 ≤ ti < ti+1 ≤ 10^6), xi, and yi (0 ≤ xi, yi ≤ 10^6) as mentioned above.
Output
For each test case, output the answer in one line.
Your answer will be considered correct if and only if its absolute or relative error is less than 1e-9.
Sample Input
2
5
2 1 9
3 7 2
5 9 0
6 6 3
7 6 0
10
11 35 67
23 2 29
29 58 22
30 67 69
36 56 93
62 42 11
67 73 29
68 19 21
72 37 84
82 24 98
Sample Output
9.2195444573
54.5893762558
Hint
In memory of the best osu! player ever Cookiezi.
Problem Idea
解题思路:
【题意】
一个游戏
在ti秒时,需点击屏幕(xi,yi)位置
游戏的难度定义:max任意相邻两次点击的距离/时间间隔
即
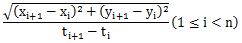
【类型】
暴力
【分析】
此题没有什么悬念,暴力就可以了
唯一需要注意的一点是,如果一开始坐标是用int型来定义的话,求距离时别因为爆int而出错就可以了
【时间复杂度&&优化】
O(N)
题目链接→HDU 5078 Osu!
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 1005;
const int M = 100005;
const int inf = 1000000007;
const int mod = 1000000007;
struct node
int t,x,y;
s[N];
double distant(node a,node b)
return sqrt(1.0*(a.x-b.x)*(a.x-b.x)+1.0*(a.y-b.y)*(a.y-b.y));
int main()
int t,n,i;
double Max;
scanf("%d",&t);
while(t--)
Max=0;
scanf("%d",&n);
for(i=0;i<n;i++)
scanf("%d%d%d",&s[i].t,&s[i].x,&s[i].y);
if(i)
Max=max(Max,distant(s[i],s[i-1])/(s[i].t-s[i-1].t));
printf("%.10f\\n",Max);
return 0;
以上是关于2014ACM/ICPC亚洲区鞍山赛区现场赛题解报告的主要内容，如果未能解决你的问题，请参考以下文章