Homography 知多少？

Posted 2022-12-05 白巧克力亦唯心

该博客内容发表在泡泡机器人公众号上，请尊重泡泡机器人公众号的版权声明

在ORB-SLAM初始化的时候，作者提到，如果场景是平面，或者近似平面，或者低视差时，我们能应用单应性矩阵(homography)，这三种情形在我应用SVO的过程中颇有同感，打破了我对$H$矩阵的固有映像，即只能用于平面或近似平面。但是我不知道如何去具体分析这里面的误差，比如不共面的情况时，应用$H$矩阵将一个图像坐标从图像1投影到图像2时，它会落在图像哪个位置？和实际位置的误差该怎么计算？误差会有多大？和哪些因素有关？另外，为何相机只做纯旋转运动时，不管平面还是非平面，$H$矩阵都能应用？等等，一些列问题，让我感觉对homography了解很粗浅。

先简单回顾我脑海里的$H$矩阵，让大家有点代入感，原谅我的啰嗦，进入正文以后就会尽量言简意赅。在没做视觉SLAM以前，通过opencv大概知道：利用两个图像中至少四个特征点能够求解一个单应性矩阵(homography matrix)，然后用这个单应性矩阵$H$能够将图像1中的某个坐标$(u,v)$变换到图像2中对应的位置$(u^{\prime },v^{\prime })$。然而，那时忽略了两个图像能够计算$H$的前提条件。在学SLAM过程中，知道$H$矩阵的推导是来自于相机在不同位姿拍摄同一个三维平面，所以使用opencv计算单应性矩阵$H$的时候前提是两个图像对应区域必须是同一平面。

最近，刘浩敏师兄的RKSLAM里面用了多$H$矩阵来提高鲁棒性，以及加上开头的那些疑问让我有迫切进一步学习$H$矩阵的想法。本文将包括三部分：$H$的由来，$H$矩阵的扩展：相机的纯旋转和非共面情形，由$H$矩阵到6点法估计本征矩阵$E$。

$H$矩阵的由来

假设相机在两个不同位姿处拍摄一个平面，该平面在frame 1中的法向量为$N$，到frame 1原点距离为$d$，具体如下图所示

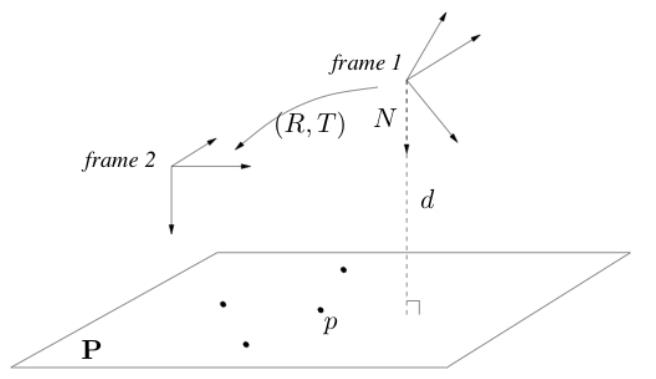
于是，坐标系1中的点可以用下式转换到坐标系2中：$${\mathbf{X}}_2=R{\mathbf{X}}_1+\mathbf{T}$$注意，大写粗体$\mathbf{X}$表示的是三维空间点。同时，由于三维点${\mathbf{X}}_1$所在平面上，由简单的直角三角形，可知该点沿着法线方向的投影距离应等于$d$：$${\mathbf{N}}^T{\mathbf{X}}_1=n_{1}X+n_{2}Y+n_{3}Z=d$$或者$$\frac{1}{d}{\mathbf{N}}^T{\mathbf{X}}_1=1\forall {\mathbf{X}}_1\in P$$结合起来我们能够得到：$${\mathbf{X}}_2=R{\mathbf{X}}_1+\mathbf{T}\frac{1}{d}{\mathbf{N}}^T{\mathbf{X}}_1=H{\mathbf{X}}_1$$所以我们就得到了平面单应性矩阵$$H=R+\mathbf{T}\frac{1}{d}{\mathbf{N}}^T,H\in {\mathbb{R}}^{3\times 3}$$回忆之前提到过本征矩阵${\mathbf{x}}_2^{T}E{\mathbf{x}}_1={\mathbf{x}}_2^T\hat{T}R{\mathbf{x}}_1=0$，它只是把点对应到一条极线，而单应性矩阵约束更强，是点到点的一一对应。

注意，本征矩阵约束公式是对于归一化图像平面坐标$\mathbf{x}=(x,y,1{)}^T$而言的，而上述推导的$H$是对三维空间点的。从3d到2d, 只需要将3d点向归一化图像平面$z=1$上投影。三维空间点到归一化图像平面只是对坐标缩放了$z$，有：$${\lambda }_1{\mathbf{x}}_1={\mathbf{X}}_1,{\lambda }_2{\mathbf{x}}_2={\mathbf{X}}_2\to {\lambda }_2{\mathbf{x}}_2=H{\lambda }_1{\mathbf{x}}_1$$从这里我们可以发现，从归一化图像平面坐标${\mathbf{x}}_2$到$H{\mathbf{x}}_1$之间还存在一个尺度因子，因此我们利用两个图像对应的坐标对能恢复$H$，但从该$H$中无法将平移$\mathbf{T}$和$d$分离出来，就导致了尺度的不确定性。而利用$H$，我们能得到${\mathbf{x}}_2\sim H{\mathbf{x}}_1$，注意虽然这里是用的相似符号，但是我们还是能得到图像坐标的一一对应，计算出$\mathbf{x}=H{\mathbf{x}}_1$以后，将$\mathbf{x}$的坐标都除以${\mathbf{x}}_z$进行坐标归一化，就能得到${\mathbf{x}}_2$。

H矩阵的扩展：相机的纯旋转和非共面情形

先看纯旋转情形，三维坐标关系如下：$${\mathbf{X}}_2=R{\mathbf{X}}_1$$对应的有 H = R + T 1 d N T , T =