排序算法（21.12）

Posted 2022-12-05 未定_

排序

• 一、基于比较的排序
• • 1.插入排序
  • • 1.1直接插入排序
    • 1.2希尔排序
  • 2.交换排序
  • • 2.1冒泡排序
    • 2.2快速排序
  • 3.选择排序
  • • 3.1简单选择排序
    • 3.2堆排序
  • 4.归并排序
  • • 二路归并排序
• 二、不基于比较的排序
• • 1.桶式排序
  • 2.基数排序
• 三、各排序算法的比较
• • 1.比较表
  • 2.分类

一、基于比较的排序

1.插入排序

无序记录-插入->有序序列

1.1直接插入排序

基本思想：

依次将待排序列中的每一个记录插入到已经排好的序列中，直到全部排好

例：12、30、25、9、18

void insertSort(int r[],int n)

    int j=0;
    for(int i=2;i<=n;i++)
    
        r[0]=r[i];
        j=i-1;
        while(r[j]>r[0])
        
            r[j+1]=r[j];
            j--;
        
        r[j+1]=r[0];
    

性能分析：

·最好的情况：初始序列是正序
比较次数：n-1
移动次数：2(n-1) (从第二项开始每一趟待排记录移到r[0]再移回来)
时间复杂度:O(n)
辅助空间:O(1)

·最坏的情况：初始序列为逆序
比较次数:${\sum }_{i=2}^{n}i$=$\frac{(n+2)(n-1)}{2}$
移动次数：${\sum }_{i=2}^{n}i+1$=$\frac{(n+4)(n-1)}{2}$
时间复杂度:O(n²)
辅助空间:O(1)

·平均情况：
比较次数：${\sum }_{i=2}^n\frac{i}{2}$=$\frac{(n+2)(n-1)}{4}$
移动次数：${\sum }_{i=2}^n\frac{i+1}{2}$=$\frac{(n+4)(n-1)}{4}$
时间复杂度:O(n²)
辅助空间:O(1)
适用于待排序记录基本有序或待排序记录个数较小的情况，是一种稳定排序算法。

基本有序： 如1，2，8，4，5，6，7，3，9，大部分数开始就在该在的位置上。（接近正序）
局部有序： 如6，7，8，9，1，2，3，4，5，局部有序不能提高直接插入排序算法的时间性能。

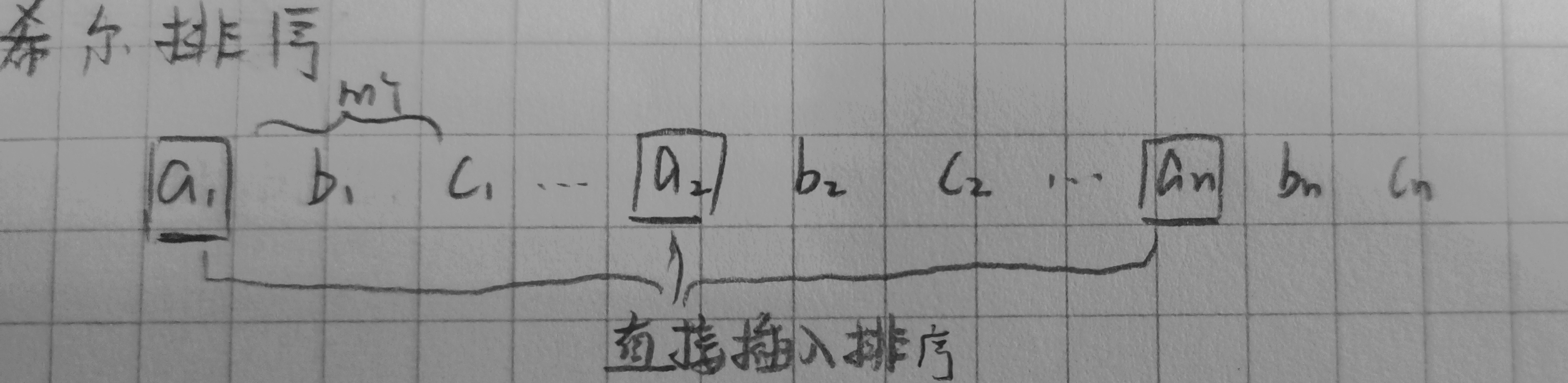
1.2希尔排序

是对直接插入排序算法的优化。

基本思想：

将整个待排记录分割成若干个子序列，子序列内分别进行直接插入排序，带整个序列记录基本有序时，对全体进行直接插入排序。（一般需要多趟）
·每趟分割组数d/2(初始d=n）

例：59、20、17、36、98、14、23、83、13、28

void ShellSort(int r[],int n)

    for(int d=n/2;d>=1;d=d/2)
    
        for(int i=d+1;i<=n;i++)
        
            r[0]=r[i];
            int j=i-d;
            while(j>0&&r[j]>r[0])
            
                r[j+d]=r[j];
                j=j-d;
            
            r[j+d]=r[0];
        
    

性能分析：
·希尔排序的趟数：
1：n/2
2：n/4
3：n/8
……
k：n/2^k
所以$\frac{n}{2^k}$>=1

希尔排序算法的时间性能是所取增量的函数，目前尚未找到最好的增量序列。
平均时间复杂度:O(nlog ₂n)~O(n²)
当n在某个特定范围内：最好的时间复杂度:O(n^1.3 ) 。最坏的时间复杂度：O(n²)
辅助空间:O(1)

是一种不稳定排序算法。

2.交换排序

r_i <—反序则交换—> r_j

2.1冒泡排序

基本思想：

两两比较相邻记录的关键码，如果反序则交换，直到没有反序的记录为止。

传统的冒泡排序：

for(j=0; j<n-1; j++)
   for(i=j+1; i<n; i++)
            if(a[j]>a[i])
            
                temp=a[j];
                a[j]=a[i];
                a[i]=temp;
            

传统的冒泡排序需要扫描n-1趟，第 i 趟至少把 i 个大数排到最后（升序排），为了使排序更优化，让已位于最终位置的大数不参与下一趟排序，需要考虑以下几点：
(1) 在一趟起泡排序中，若有多个记录位于最终位置，应如何记载？
(2) 如何确定起泡排序的范围，使得已经位于最终位置的记录不参与下一趟排序？
(3)如何判别起泡排序的结束？
解决：(1) 设变量exchange记载记录交换的位置，一趟排序后，exchange记载的一趟排序中记录的最后一次交换的位置，exchange位置之后的记录都有序。
(2) 设bound表示无序区的最后一个记录，则每趟起泡排序的范围是r[1] ~ r[bound]。在一趟排序后，bound=exchange。
(3) 每趟排序exchange的初值为0，若交换其值大于0。

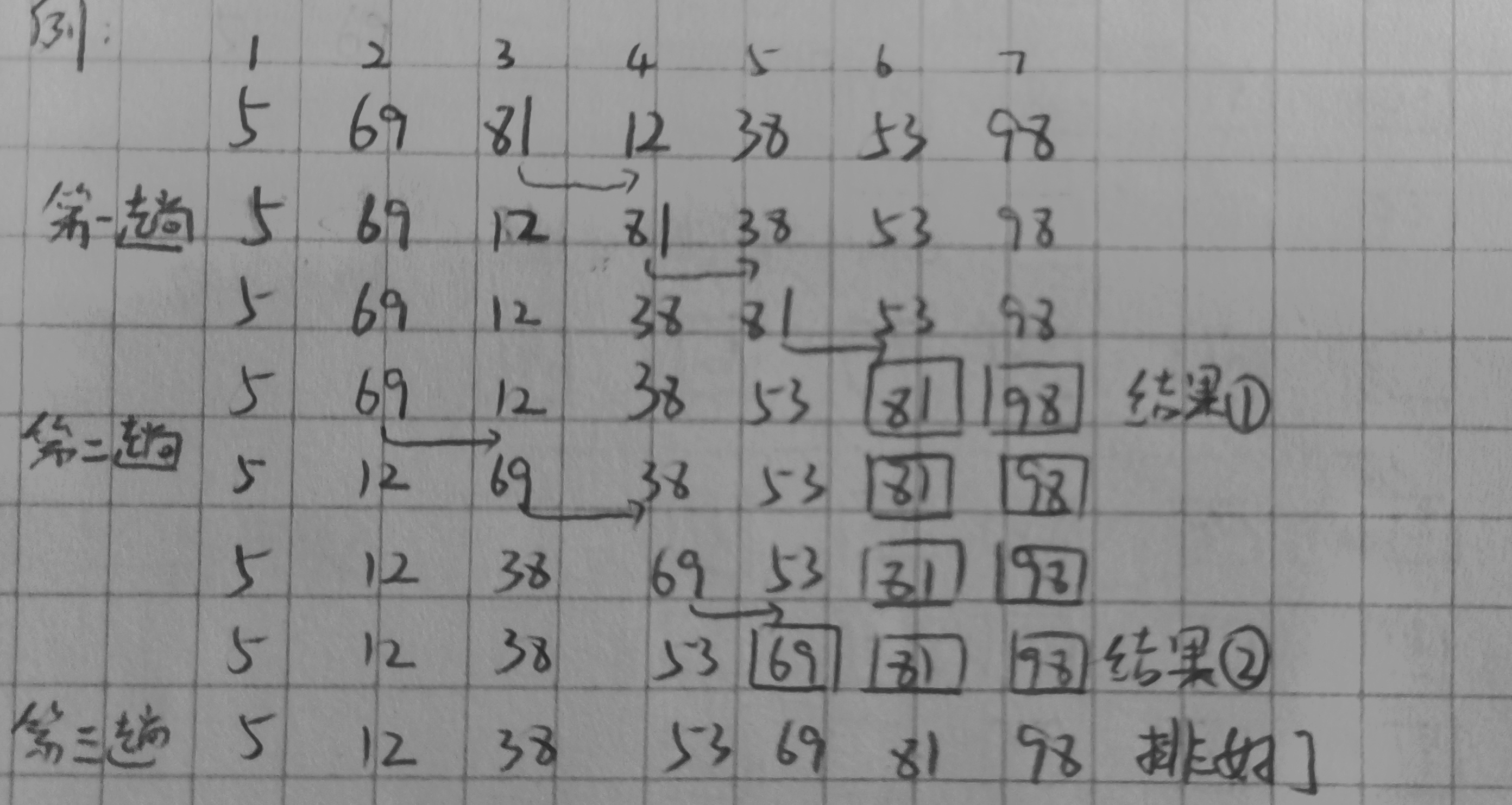
例：5、69、 81、12、38、53、98

void BubbleSort(int r[],int n)

    int exchange=n,bound;
    while(exchange)
    
        bound=exchange;
        exchange=0;
        for(int j=1;j<bound;j++)
        
            if(r[j]>r[j+1])
            
                int t=r[j];
                r[j]=r[j+1];
                r[j+1]=t;
                exchange=j;
            
        
    

性能分析：
·最好的情况：初始序列是正序
比较次数：n-1
移动次数：0
时间复杂度:O(n)
辅助空间:O(1)

·最坏的情况：初始序列为逆序
比较次数:${\sum }_{i=1}^{n-1}(n-i)$=$\frac{n(n-1)}{2}$
移动次数：${\sum }_{i=1}^{n-1}3(n-i)$=$\frac{3n(n-1)}{2}$（比较1次移动3次）
例如：
5-4-3-2-1
4-3-2-1 5
3-2-1 4 5
2-1 3 4 5
1 2 3 4 5
时间复杂度:O(n²)
辅助空间:O(1)
·平均情况：
时间复杂度:O(n²)
辅助空间:O(1)
每趟至少把一个最大或最小排到序列的末端，是一种稳定排序算法。

2.2快速排序

基本思想：

选轴值，一趟排序将待排序记录分割成两部分，轴值前一部分记录的关键码均小于或等于轴值，轴值后一部分记录的关键码均大于或等于轴值，重复上述方法，直到整个序列有序。

一般选第一个数作为轴值，轴值最好在序列的位置是居中的，如果待排序列是正序或逆序（最坏的情况），比较序列中第一个记录、最后一个记录和中间记录的关键码，取关键码居中的作为轴值并调换到第一个位置。
选取不同轴值的后果：
决定两个子序列的长度，子序列的长度最好相等。

例：38、27、55、50、13、49、65

int Partition(int r[],int first,int end)//一次划分

    int i=first,j=end;
    r[0]=r[i];
    while(i<j)
    
        while(i<j&&r[0]<=r[j])
            j--;
        if(i<j)
        
            r[i]=r[j];
            i++;
        
        while(i<j&&r[i]<=r[0])
            i++;
        if(i<j)
        
            r[j]=r[i];
            j--;
        
    
    r[i]=r[0];
    return i;

void QuickSort(int r[],int first,int end)

    if(first>=end)//一定要大于等于
        return;
    int f=Partition(r,first,end);
    QuickSort(r,first,f-1);
    QuickSort(r,f+1,end);

性能分析：

执行时间取决于递归的深度
·最好的情况：每次划分左右侧子序列的长度都相等。
扫描时间：O(n)
排序时间：O(nlog₂n)

·最坏的情况：初始序列为正序或逆序
比较次数:${\sum }_{i=1}^{n-1}(n-i)$=$\frac{n(n-1)}{2}$=O(n²)
移动次数：小于比较次数
时间复杂度:O(n²)

·平均情况：
时间复杂度:O(nlog₂n)
辅助空间:O(log₂n)~O(n)
是内排序算法中最好的，适用于待排数据量教大的情况，是一种不稳定排序算法。

3.选择排序

有序序列<-加入-选择最小记录
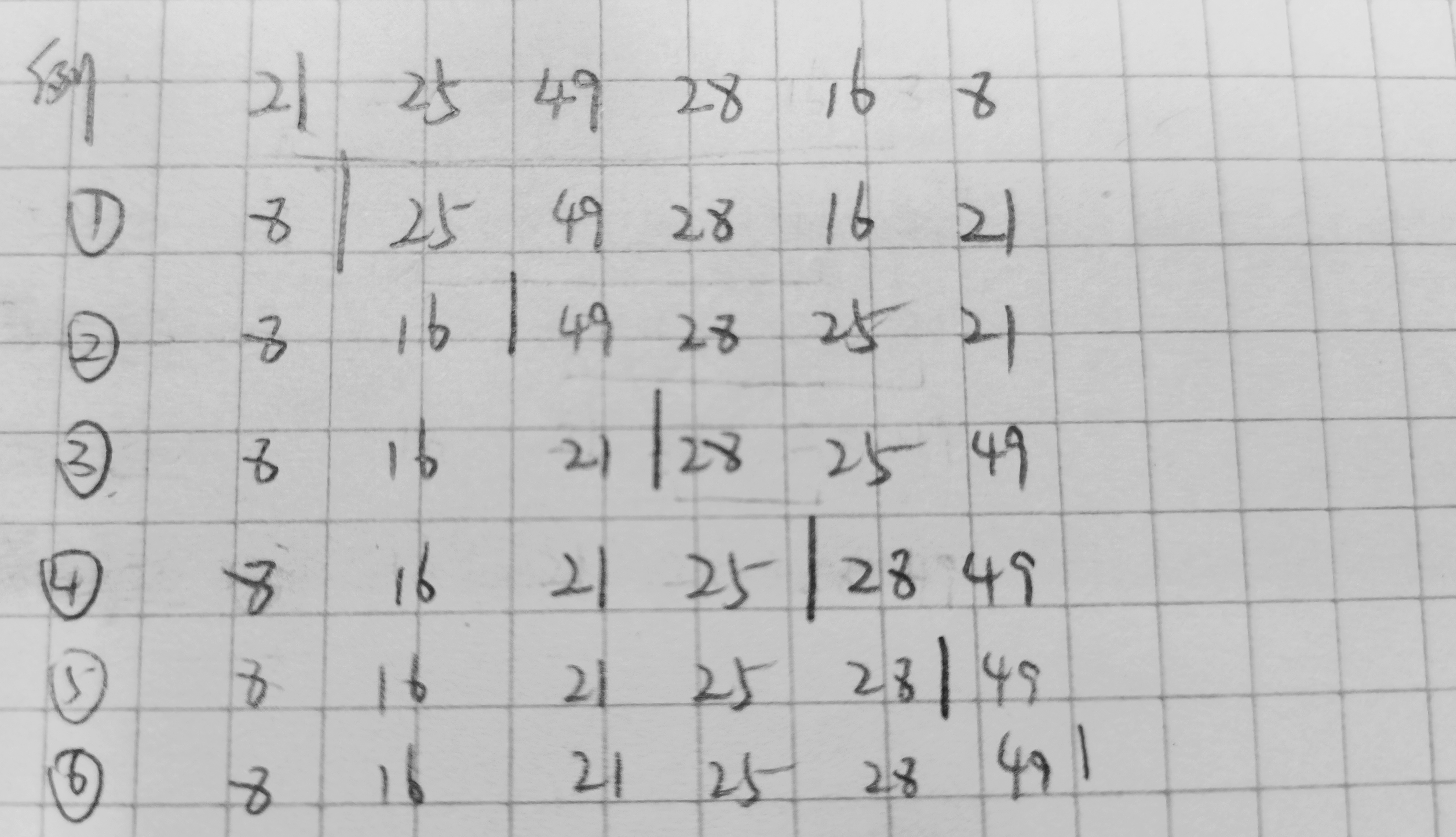
选择排序的工作原理是每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

3.1简单选择排序

基本思想：

int selectSort(int r[],int n)

    for(int i=1; i<n; i++)
    
        int index=i;
        for(int j=i+1; j<=n; j++)
            if(r[j]<r[index])
                index=j;
        if(index!=i)
        
            int t=以上是关于排序算法（21.12）的主要内容，如果未能解决你的问题，请参考以下文章
 
 查找技术（21.12）
 查找技术（21.12）
 查找技术（21.12）
 排序算法——冒泡排序
 排序算法——冒泡排序
 算法采用递归方式实现按升序排序的选择排序算法（C++源码）