2016ACM/ICPC亚洲区沈阳站现场赛题解报告
Posted queuelovestack
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了2016ACM/ICPC亚洲区沈阳站现场赛题解报告相关的知识，希望对你有一定的参考价值。
此文章可以使用目录功能哟↑(点击上方[+])
打了一下沈阳重现,虽说05时限变小了,但是对于我这种水不出题的人来说,根本原因还是自己太弱...
说句题外话,羡慕学魔老师能够靠出题赚钱
Problem 1001 Thickest Burger
Accept: 0 Submit: 0
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Problem Description
ACM ICPC is launching a thick burger. The thickness (or the height) of a piece of club steak is A (1 ≤ A ≤ 100). The thickness (or the height) of a piece of chicken steak is B (1 ≤ B ≤ 100).
The chef allows to add just three pieces of meat into the burger and he does not allow to add three pieces of same type of meat. As a customer and a foodie, you want to know the maximum total thickness of a burger which you can get from the chef. Here we ignore the thickness of breads, vegetables and other seasonings.
Input
The first line is the number of test cases. For each test case, a line contains two positive integers A and B.
Output
For each test case, output a line containing the maximum total thickness of a burger.
Sample Input
10
68 42
1 35
25 70
59 79
65 63
46 6
28 82
92 62
43 96
37 28
Sample Output
178
71
165
217
193
98
192
246
235
102
Hint
Consider the first test case, since 68+68+42 is bigger than 68+42+42 the answer should be
68+68+42 = 178.
Similarly since 1+35+35 is bigger than 1+1+35, the answer of the second test case should be
1+35+35 = 71.
Problem Idea
解题思路:
【题意】
这个题目意思，一开始，我是拒绝的，因为我真的看不懂(╭(╯^╰)╮不要嘲笑我英语差)
所以投机了一波(￣へ￣直接看样例)
题目意思是，牛排层的厚度是A，鸡排层的厚度是B，面包层、蔬菜层及调味料的厚度忽略
现在要做一个汉堡，你可以往里面加三层肉类层(鸡排层或牛排层)
问汉堡总厚度最大为多少，要求三层肉类层不能是同一种类型(即不能三层都是牛排层或三层都是鸡排层)
【类型】
一号签到题
【分析】
由于三层肉类层不能是同一类型
所以最初什么都不考虑，牛排层和鸡排层先各来一层
剩下的那层，哪种类型比较厚，就选哪种
故结果为A+B+max(A,B)
【时间复杂度&&优化】
O(T)
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<list>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 100005;
const int M = 100005;
const int inf = 1000000007;
const int mod = 1000000007;
int main()
int t,A,B;
scanf("%d",&t);
while(t--)
scanf("%d%d",&A,&B);
printf("%d\\n",A+B+max(A,B));
return 0;
Problem 1002 Relative atomic mass
Accept: 0 Submit: 0
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Problem Description
Relative atomic mass is a dimensionless physical quantity, the ratio of the average mass of atoms of an element (from a single given sample or source) to 1/2 of the mass of an atom of carbon-12 (known as the unified atomic mass unit).
You need to calculate the relative atomic mass of a molecule, which consists of one or several atoms. In this problem, you only need to process molecules which contain hydrogen atoms, oxygen atoms, and carbon atoms. These three types of atom are written as ’H’，’O’ and ’C’ repectively. For your information, the relative atomic mass of one hydrogen atom is 1, and the relative atomic mass of one oxygen atom is 16 and the relative atomic mass of one carbon atom is 12. A molecule is demonstrated as a string, of which each letter is for an atom. For example, a molecule ’HOH’ contains two hydrogen atoms and one oxygen atom, therefore its relative atomic mass is 18 = 2 * 1 + 16.
Input
The first line of input contains one integer N(N ≤ 10), the number of molecules. In the next N lines, the i-th line contains a string, describing the i-th molecule. The length of each string would not exceed 10.
Output
For each molecule, output its relative atomic mass.
Sample Input
5
H
C
O
HOH
CHHHCHHOH
Sample Output
1
12
16
18
46
Problem Idea
解题思路:
【题意】
给你一个长度不超过10的字符串表示一种分子
问该分子的相对原子质量为多少
其中，H的相对原子质量为1，C的相对原子质量为12，O的相对原子质量为16
【类型】
二号签到题
【分析】
简单的字符串处理题
字符'H'的贡献为1，字符'C'的贡献为12，字符'O'的贡献为16，遍历一遍
计算整个字符串的贡献和即可
【时间复杂度&&优化】
O(T*strlen(s))
题目链接→HDU 5949 Relative atomic mass
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<list>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 15;
const int M = 100005;
const int inf = 1000000007;
const int mod = 1000000007;
char s[N];
int main()
int n,i,ans;
scanf("%d",&n);
while(n--)
ans=0;
scanf("%s",s);
for(i=0;s[i]!='\\0';i++)
if(s[i]=='H')
ans++;
else if(s[i]=='C')
ans+=12;
else
ans+=16;
printf("%d\\n",ans);
return 0;
Problem 1003 Recursive sequence
Accept: 0 Submit: 0
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Problem Description
Farmer John likes to play mathematics games with his N cows. Recently, they are attracted by recursive sequences. In each turn, the cows would stand in a line, while John writes two positive numbers a and b on a blackboard. And then, the cows would say their identity number one by one. The first cow says the first number a and the second says the second number b. After that, the i-th cow says the sum of twice the (i-2)-th number, the (i-1)-th number, and i^4. Now, you need to write a program to calculate the number of the N-th cow in order to check if John’s cows can make it right.
Input
The first line of input contains an integer t, the number of test cases. t test cases follow.
Each case contains only one line with three numbers N, a and b where N,a,b < 2^31 as described above.
Output
For each test case, output the number of the N-th cow. This number might be very large, so you need to output it modulo 2147493647.
Sample Input
2
3 1 2
4 1 10
Sample Output
85
369
Hint
In the first case, the third number is 85 = 2*1十2十3^4.
In the second case, the third number is 93 = 2*1十1*10十3^4 and the fourth number is
369 = 2 * 10 十 93 十 4^4.
Problem Idea
解题思路:
【题意】
F(1)=a，F(2)=b，F(N)=2F(N-2)+F(N-1)+N^4
给你N,a,b(N,a,b < 2^31)
求F(N)%2147493647
【类型】
推导+矩阵快速幂
【分析】
知道矩阵快速幂的小伙伴应该都比较熟悉这种类型的题了吧
如果递推式是F(N)=2F(N-2)+F(N-1)就方便了许多，基本的矩阵快速幂
但是现在多了一项系数项N^4
矩阵快速幂就不能直接用了，需要做进一步推导
但是小伙伴们也不需要着急，我会一步步解释
矩阵快速幂能否可以使用，取决于任意相邻状态是不是可以通过相同的系数阵得到
例如递推式F(N)=2F(N-2)+F(N-1)，它的任意一项都可以通过前一项右乘系数阵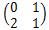
得到
所以此题关键也是要求出对应的系数阵
而系数阵跟相邻两项有关
假设我们现在知道N^4的第i项i^4,那么该如何得到第i+1项(i+1)^4呢?
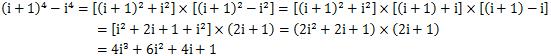
这时，又产生了i^3,i^2,i这些新项需要我们计算
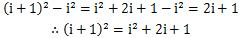
于是，我们可以得到矩阵式
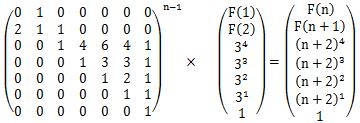
然后套一波矩阵快速幂的模板就可以了
本人比较笨的手动把系数阵输了一遍，当然你可以循环输入，毕竟系数阵下面五行是倒杨辉三角
另外，本题有个坑点就是，2147493647已经超过了int的范围，所以需注意这里不要犯错
【时间复杂度&&优化】
O(logn)
题目链接→HDU 5950 Recursive sequence
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<list>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 7;
const int M = 40;
const int inf = 1000000007;
const __int64 mod = 2147493647;
typedef struct node
__int64 a[N][N];
void Init()
memset(a,0,sizeof(a));
for(int i=0;i<N;i++)
a[i][i]=1;
matrix;
matrix mul(matrix a,matrix b)//矩阵乘法
matrix ans;
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
ans.a[i][j]=0;
for(int k=0;k<N;k++)
ans.a[i][j]+=(a.a[i][k]*b.a[k][j])%mod;
ans.a[i][j]%=mod;
return ans;
matrix pow(matrix a,int n)//求a^n
matrix ans;
ans.Init();
while(n)
if(n%2)
ans=mul(ans,a);
n/=2;
a=mul(a,a);
return ans;
int main()
int t;
__int64 n,a,b;
matrix ans,s;
scanf("%d",&t);
while(t--)
scanf("%I64d%I64d%I64d",&n,&a,&b);
memset(ans.a,0,sizeof(ans.a));
ans.a[0][0]=a%mod;
ans.a[1][0]=b%mod;
ans.a[2][0]=81;
ans.a[3][0]=27;
ans.a[4][0]=9;
ans.a[5][0]=3;
ans.a[6][0]=1;
s.a[0][0]=0;s.a[0][1]=1;s.a[0][2]=0;s.a[0][3]=0;s.a[0][4]=0;s.a[0][5]=0;s.a[0][6]=0;//a
s.a[1][0]=2;s.a[1][1]=1;s.a[1][2]=1;s.a[1][3]=0;s.a[1][4]=0;s.a[1][5]=0;s.a[1][6]=0;//b
s.a[2][0]=0;s.a[2][1]=0;s.a[2][2]=1;s.a[2][3]=4;s.a[2][4]=6;s.a[2][5]=4;s.a[2][6]=1;//i^4
s.a[3][0]=0;s.a[3][1]=0;s.a[3][2]=0;s.a[3][3]=1;s.a[3][4]=3;s.a[3][5]=3;s.a[3][6]=1;//i^3
s.a[4][0]=0;s.a[4][1]=0;s.a[4][2]=0;s.a[4][3]=0;s.a[4][4]=1;s.a[4][5]=2;s.a[4][6]=1;//i^2
s.a[5][0]=0;s.a[5][1]=0;s.a[5][2]=0;s.a[5][3]=0;s.a[5][4]=0;s.a[5][5]=1;s.a[5][6]=1;//i^1
s.a[6][0]=0;s.a[6][1]=0;s.a[6][2]=0;s.a[6][3]=0;s.a[6][4]=0;s.a[6][5]=0;s.a[6][6]=1;//1
ans=mul(pow(s,n-1),ans);
printf("%I64d\\n",ans.a[0][0]);
return 0;
Problem 1005 Counting Cliques
Accept: 0 Submit: 0
Time Limit: 8000/4000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Problem Description
A clique is a complete graph, in which there is an edge between every pair of the vertices. Given a graph with N vertices and M edges, your task is to count the number of cliques with a specific size S in the graph.
Input
The first line is the number of test cases. For each test case, the first line contains 3 integers N,M and S (N ≤ 100,M ≤ 1000,2 ≤ S ≤ 10), each of the following M lines contains 2 integers u and v (1 ≤ u < v ≤ N), which means there is an edge between vertices u and v. It is guaranteed that the maximum degree of the vertices is no larger than 20.
Output
For each test case, output the number of cliques with size S in the graph.
Sample Input
3
4 3 2
1 2
2 3
3 4
5 9 3
1 3
1 4
1 5
2 3
2 4
2 5
3 4
3 5
4 5
6 15 4
1 2
1 3
1 4
1 5
1 6
2 3
2 4
2 5
2 6
3 4
3 5
3 6
4 5
4 6
5 6
Sample Output
3
7
15
Problem Idea
解题思路:
【题意】
现有一个n个结点m条边的无向图
问该图中有多少个由s个点构成的完全子图
保证图中每个结点的度都不会超过20
【类型】
dfs搜索+剪枝
【分析】
从每个点出发，将可能(即与已在完全子图内的结点直接相连)成为完全子图的点加入其中，同时更新这个完全子图中的点数和那些点，直到完全子图中的点数达到s时返回。
【时间复杂度&&优化】
恕本人愚钝,深搜的复杂度真不会算
题目链接→HDU 5952 Counting Cliques
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<list>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 105;
const int M = 1005;
const int inf = 1000000007;
const int mod = 1000000007;
struct edge
int v,to;
e[M];
int s,k,p,h[N],degree[N],point[N];
__int64 ans;
bool g[N][N],vis[N];
void add_edge(int u,int v)
e[p].v=v;
e[p].to=h[u];
h[u]=p++;
void dfs(int u)
if(k==s)//完全子图内的结点数达到s
ans++;
return ;
for(int i=h[u];i+1;i=e[i].to)
int v=e[i].v,j;
if(degree[v]<s-1)//度不够的结点可以直接舍弃
continue;
for(j=0;j<k;j++)//判断该点是否与所有已在完全子图内的结点直接相连
if(!g[v][point[j]])
break;
if(j>=k)
point[k++]=v;//将点v加入完全子图
dfs(v);
point[--k]=0;//将点v从完全子图中去除
int main()
int t,n,m,i,j,u,v;
scanf("%d",&t);
while(t--)
p=0;ans=0;
memset(h,-1,sizeof(h));
memset(g,false,sizeof(g));
memset(degree,0,sizeof(degree));
scanf("%d%d%d",&n,&m,&s);
for(i=0;i<m;i++)
scanf("%d%d",&u,&v);
g[u][v]=g[v][u]=true;
degree[u]++;
degree[v]++;
if(u>v)
swap(u,v);
add_edge(u,v);
for(i=1;i<=n;i++)
if(degree[i]<s-1)//度不够的结点可以直接舍弃
continue;
k=0;
point[k++]=i;//将点i加入完全子图
dfs(i);
printf("%I64d\\n",ans);
return 0;
以上是关于2016ACM/ICPC亚洲区沈阳站现场赛题解报告的主要内容，如果未能解决你的问题，请参考以下文章