LeetCode 0509. 斐波那契数：尝试以四种方式吃透（四种大方法+两种小优化）

Posted 2022-12-04 Tisfy

【LetMeFly】尝试以四种方式吃透：509.斐波那契数（四种大方法+两种小优化）

先说明本题解法：

1. 动态规划（及 原地滚动的优化）
2. 递归（及 记忆化的优化）
3. 矩阵快速幂
4. 通项公式

---

力扣题目链接：https://leetcode.cn/problems/fibonacci-number/

斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1

给定 n ，请计算 F(n) 。

 

示例 1：

输入：n = 2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1

示例 2：

输入：n = 3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2

示例 3：

输入：n = 4
输出：3
解释：F(4) = F(3) + F(2) = 2 + 1 = 3

 

提示：

• 0 <= n <= 30

方法一：动态规划

开辟一个大小为$30$的数组$a$（或开辟大小为$n+1$的数组也可）

初始值$a[0]=0,a[1]=1$

之后从下标$2$开始到$n$为止，使用转移方程$a[n]=a[n-1]+a[n-2]$求解

最终返回a[n]即可

• 时间复杂度$O(n)$
• 空间复杂度$O(C)$，这里$C$是数据中$n$的最大值$30$（也可以只开辟$n+1$的数组，则空间复杂度为$O(n)$）

AC代码

C++

class Solution   // 开辟一整个数组
public:
    int fib(int n) 
        int a[31] = 0, 1;
        for (int i = 2; i <= n; i++)
            a[i] = a[i - 1] + a[i - 2];
        return a[n];
    
;

方法一.2：动态规划 + 原地滚动

不难发现，在计算$a[n]$时，我们只用到了$a[n-1]$和$a[n-2]$，再往前的数据就再也用不到了

因此，我们只需要使用两个额外的空间${}_0$和${}_1$来分别记录$a[n-1]$和a[n-2]$的值，在计算过程中，不断更新$_0$和$_1$的值即可

• 时间复杂度$O(n)$
• 空间复杂度$O(1)$

AC代码

C++

class Solution   // 两个额外变量模拟
public:
    int fib(int n) 
        if (n < 2)
            return n;
        int _0 = 0, _1 = 1;  // 分别代表a[n - 2]和a[n - 1]
        int ans;
        for (int i = 2; i <= n; i++) 
            ans = _0 + _1;
            _0 = _1, _1 = ans;  // Update
        
        return ans;
    
;

方法二：递归

斐波那契数列很容易看出“递归”

题目都说明了，$F(n)=F(n-1)+F(n-2)$，终止条件是$n=0$或$n=1$

那么，我们只需要在非终止条件下无脑递归即可。

• 时间复杂度$O(n^2)$，这个时间复杂度待会儿分析
• 空间复杂度$O(n)$，不论总递归次数为多少，总递归深度为$n$

AC代码

C++

class Solution   // 递归
public:
    int fib(int n) 
        if (n < 2)
            return n;
        return fib(n - 1) + fib(n - 2);
    
;

方法二.2：递归 + 记忆化

方法二在数据量小的前提下能很轻松地计算出结果。

但是为什么方法二的时间复杂度是$O(n^2)$呢？

不难发现，计算$F(5)$时，会调用$F(4)$和$F(3)$，但在计算$F(4)$时，会再调用一次$F(3)$，也就是说$F(3)$不只被调用了一次

例如计算$F(6)$时：

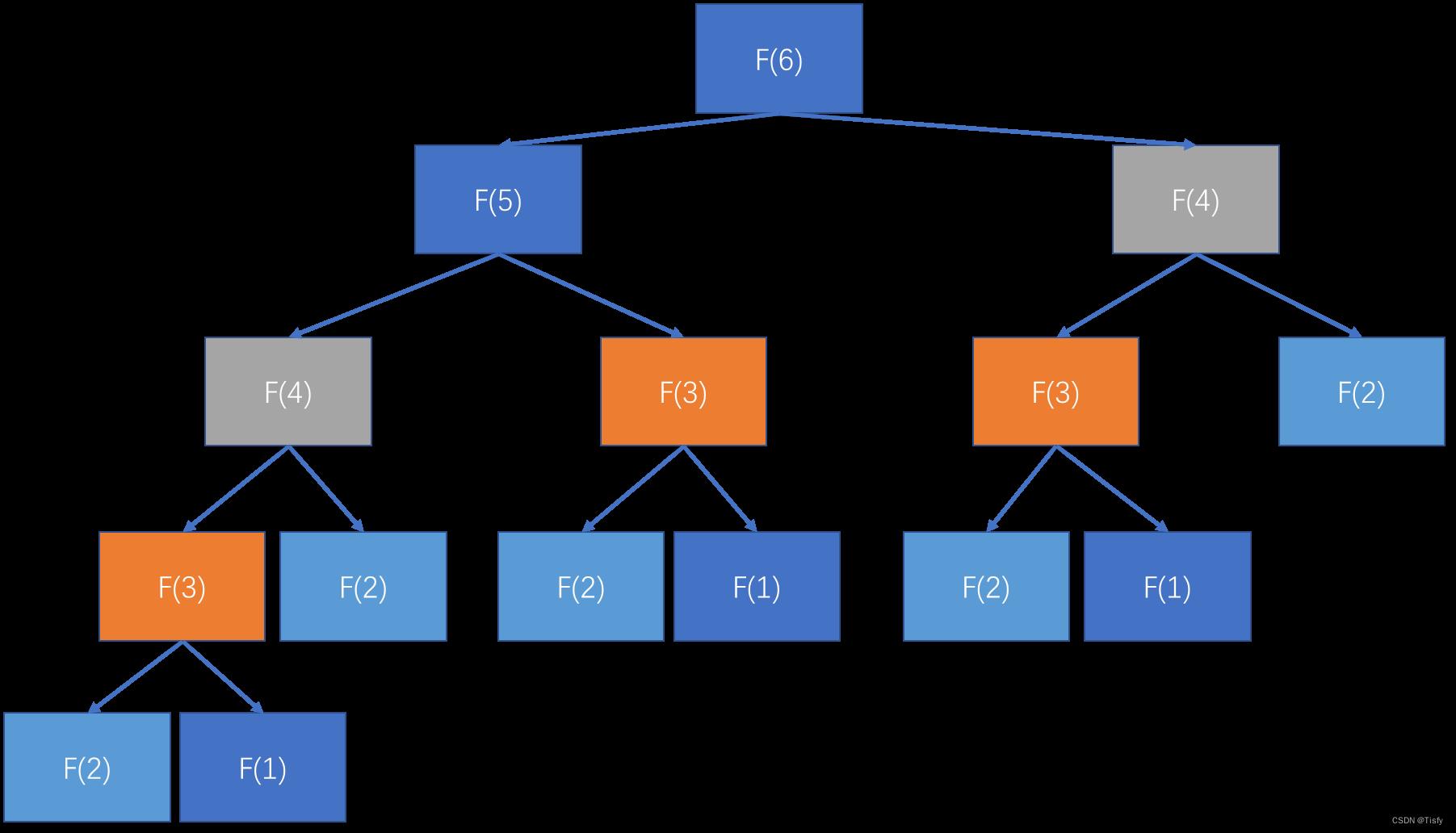
$F(4)$计算了两次，$F(3)$计算了三次，$F(2)$更是计算了五次。

$n$越大，这种重复计算就越明显。

那么，既然算过一遍$F(3)$了，为什么要再算一次呢？

记忆化出现了

我们使用一个哈希表，将计算过的结果记录下来，那么再次调用这个函数时，直接返回之前计算过的结果不就可以了吗？

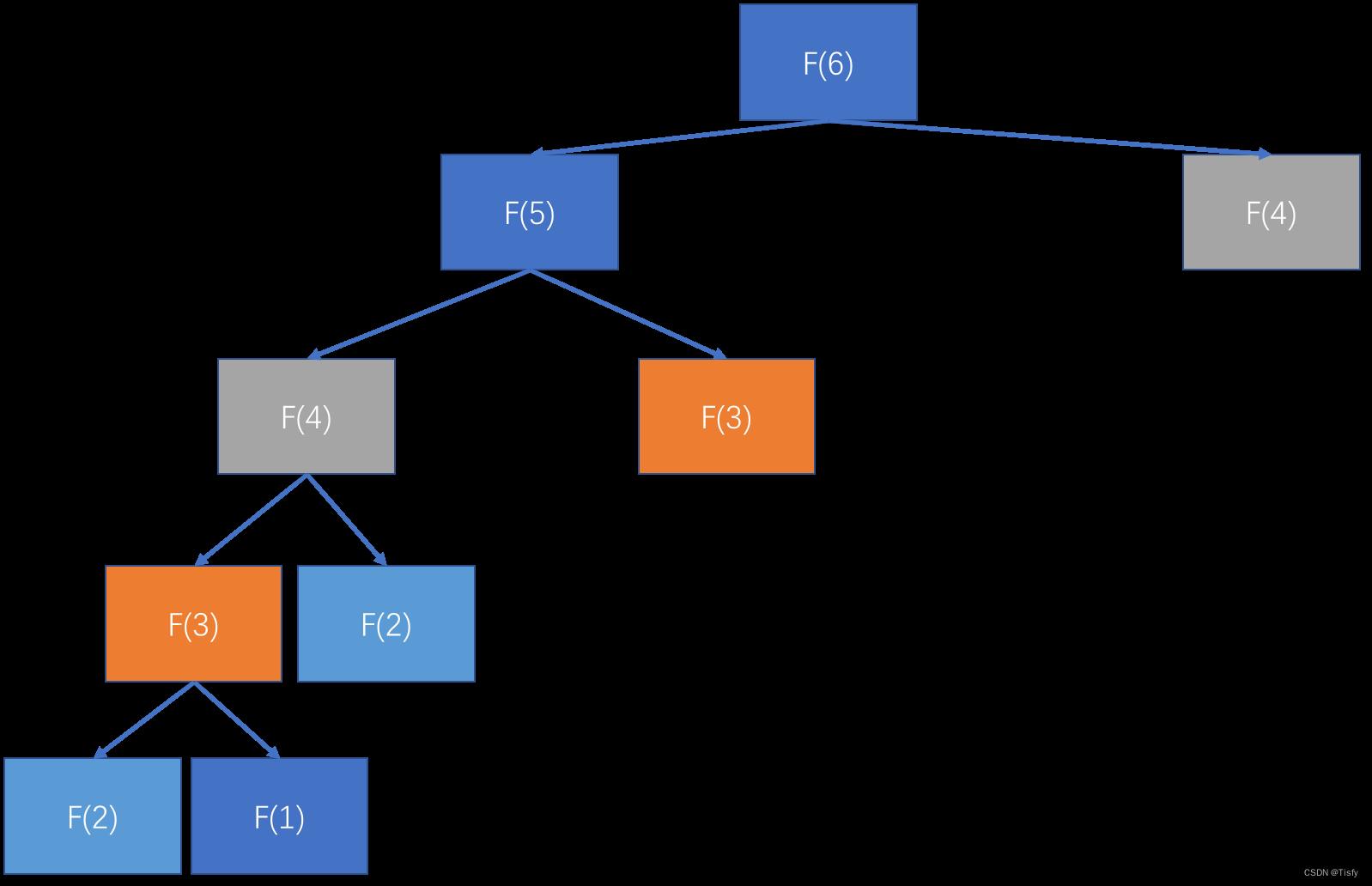
这样就避免了没必要的重复计算。

• 时间复杂度$O(n)$
• 空间复杂度$O(n)$

AC代码

C++

class Solution   // 递归 + 记忆化
private:
    unordered_map<int, int> ma;
public:
    int fib(int n) 
        if (n < 2)
            return n;
        if (ma.count(n))
            return ma[n];
        return ma[n] = fib(n - 1) + fib(n - 2);
    
;

方法三：矩阵快速幂

$$\left[\begin{array}{ll}1& 1\\ 1& 0\end{array}\right]\left[\begin{array}{c}{a}_n\\ a_{n-1}\end{array}\right]=\left[\begin{array}{c}{a}_n+a_{n-1}\\ a_n\end{array}\right]=\left[\begin{array}{c}{a}_{n+1}\\ a_n\end{array}\right]$$

因此

$$\left[\begin{array}{c}{a}_{n+1}\\ a_n\end{array}\right]={\left[\begin{array}{ll}1& 1\\ 1& 0\end{array}\right]}^n\left[\begin{array}{l}{a}_1\\ a_0\end{array}\right]$$

因此可以使用矩阵快速幂求出

[ 1 1