超级简单的机器学习入门

Posted 2022-12-02 叫我胡萝北

超级简单的机器学习入门

文章目录

• 超级简单的机器学习入门
• • 0.写在前面
  • 1.机器学习基本概念
  • 2.机器学习算法的类型
  • • 2.1 监督学习
    • 2.2 无监督学习
    • 2.3 监督学习和无监督学习的对比
    • 2.4 强化学习
  • 3.机器学习的三个基本要素
  • • 3.1 模型
    • 3.2 学习准则
    • • 3.2.1 损失函数
      • 3.2.2 欠拟合和过拟合（包含正则化）
    • 3.3 优化方法
    • • 3.3.1 梯度下降法（重要！）
      • 3.3.2 数据预处理
      • 3.3.3 提前停止
      • 3.3.4 超参数优化
  • 4.线性模型
  • • 4.1 感知器
    • 4.2 Logistic回归
    • 4.3 Softmax回归
    • 4.4 支持向量机
    • • 4.4.1 参数学习
      • 4.4.2 核函数
      • 4.4.3 软间隔
    • 4.5 损失函数对比
  • 5. 写在最后

0.写在前面

本文大多数内容来自《神经网络与深度学习》（邱锡鹏，神经网络与深度学习，机械工业出版社，https://nndl.github.io/, 2020.）周志华-机器学习，也参考了很多其他笔记博客。仅作为学习记录。

1.机器学习基本概念

① 机器学习是什么？

机器学习就是让计算机从数据中进行自动学习，得到某种知识或规律。

② 样本和数据集

​我们可以将一个标记好特征以及标签看作一个样本。

​一组样本构成的集合称为数据集。一般将数据集分为两部分：训练集和测试集。

​训练集中的样本是用来训练模型的，而测试集中的样本是用来检验模型好坏的。

③ 学习与训练

​ 我们通常用一个𝐷 维向量$$\mathbf{x}=[x_1,x_2,\cdots ,x_D{]}^T$$ 表示所有特征构成的向量，称为特征向量，其中每一维表示一个特征。

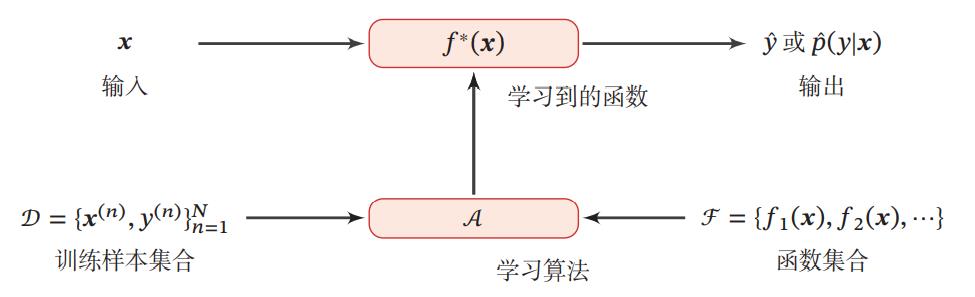
​ 假设训练集 𝒟 由 𝑁 个样本组成，其中每个样本都是独立同分布的，计为：$$\mathcal{D}=({\mathbf{x}}^{(1)},y^{(1)}),({\mathbf{x}}^{(2)},y^{(2)}),\cdots ,({\mathbf{x}}^{(N)},y^{(N)}).$$

​ 我们希望让计算机从一个函数集合$$\mathcal{F}=f_1(\mathbf{x}),f_2(\mathbf{x}),\cdots$$ 中自动寻找一个“最优”的函数𝑓∗(𝒙) 来近似每个样本的特征向量 𝒙 和标签 𝑦 之间的真实映射关系，找到这个最优函数的过程就叫做学习或训练。

以下给出一个学习的基本流程：

​ 通过训练集，不断识别特征，不断建模，最后形成有效的模型，这个过程就叫“机器学习”！

2.机器学习算法的类型

2.1 监督学习

​如果机器学习的目标是建模样本的特征 𝒙 和标签 𝑦 之间的关系，并且训练集中每个样本都有标签，那么这类机器学习称为监督学习。

​根据标签类型的不同，监督学习又可以分为回归问题、分类问题和结构化学习问题。

​ （1） 回归问题中的标签 𝑦 是连续值， 𝑓(𝒙; 𝜃)的输出也是连续值。比如未来几年预测房屋价格的走势，价格是一个连续的值。最后会按照顺序把输出值串接起来，构成一个曲线。

一元线性回归
一元线性回归是最简单，最基础的一种模型，是探究两个变量之间关系的一种统计分析方法。其模型为为：
$$y=ax+b$$其中$x$为自变量，$y$为因变量，$a$和$b$为回归系数
求解方法为最小二乘法
$$\begin{array}{l}a=\frac{{\sum }_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{{\sum }_{i=1}^n{\left(x_i-\bar{x}\right)}^2}\\ b=\bar{y}-a\bar{x}\end{array}$$

多元线性回归
探究一个因变量和多个自变量之间关系的一种统计分析方法​，其模型为：
$$y=a_l{x}_1+a_2{x}_2+\dots +a_n{x}_n+b$$其中$y$为因变量，$x_1,x_2,\dots ,x_n为自变量$，$a_1,a_2,a_3\dots ,a_n,b$ 为回归系数
求解方法类似一元线性回归，使用最小二乘法
利用线性代数的形式，对多元线性回归的误差公式求导为：
$$\begin{array}{rl}\frac{\partial \mathcal{R}(\mathbf{w})}{\partial \mathbf{w}}& =\frac{1}{2}\frac{\partial {\Vert \mathbf{y}-{\mathbf{X}}^{\top }\mathbf{w}\Vert }^2}{\partial \mathbf{w}}\\ & =-\mathbf{X}\left(\mathbf{y}-{\mathbf{X}}^{\top }\mathbf{w}\right)\end{array}$$令 $\frac{\partial }{\partial \mathbf{w}}\mathcal{R}(\mathbf{w})=0$ , 得到最优的参数 ${\mathbf{w}}^{\ast }$ 为： w ∗ = ( X X ⊤ ) − 1

以上是关于超级简单的机器学习入门的主要内容，如果未能解决你的问题，请参考以下文章

机器学习解释对偶的概念及SVM中的对偶算法？(面试回答)

机器学习笔记二十：拉格朗日函数/对偶

机器学习100天（四十一）：041 对偶支持向量机-公式推导

机器学习+优化问题的种类如何优化凸优化非凸优化对偶问题KKT条件

Andrew Ng机器学习笔记+Weka相关算法实现SVM和原始对偶问题

机器学习SVM面试题：简单介绍一下SVM？支持向量机SVM逻辑回归LR决策树DT的直观对比和理论对比，该如何选择？SVM为什么采用间隔最大化？为什么要将求解SVM的原始问题转换为其对偶问题？