生成对抗网络(GAN)简单梳理

Posted 2022-12-02 时光杂货店

作者：xg123321123 - 时光杂货店

出处：http://blog.csdn.net/xg123321123/article/details/78034859

声明：版权所有，转载请联系作者并注明出处

网上已经贴满了关于GAN的博客，写这篇帖子只是梳理下思路，以便以后查阅。
关于生成对抗网络的第一篇论文是Generative Adversarial Networks

0 前言

GAN(Generative Adversarial Nets)是用对抗方法来生成数据的一种模型。和其他机器学习模型相比，GAN引人注目的地方在于给机器学习引入了对抗这一理念。

回溯地球生物的进化路线就会发现，万物都是在不停的和其他事物对抗中成长和发展的。
生成对抗网络就像我们玩格斗游戏一样：学习过程就是不断找其他对手对抗，在对抗中积累经验，提升自己的技能。

GAN 是生成模型的一种，生成模型就是用机器学习去生成我们想要的数据，正规的说法是，获取训练样本并训练一个模型，该模型能按照我们定义的目标数据分布去生成数据。

比如autoencoder自编码器，它的decoding部分其实就是一种生成模型，它是在生成原数据。又比如seq2seq序列到序列模型，其实也是生成另一个我们想要的序列。Neural style transfer的目标其实也是生成图片。

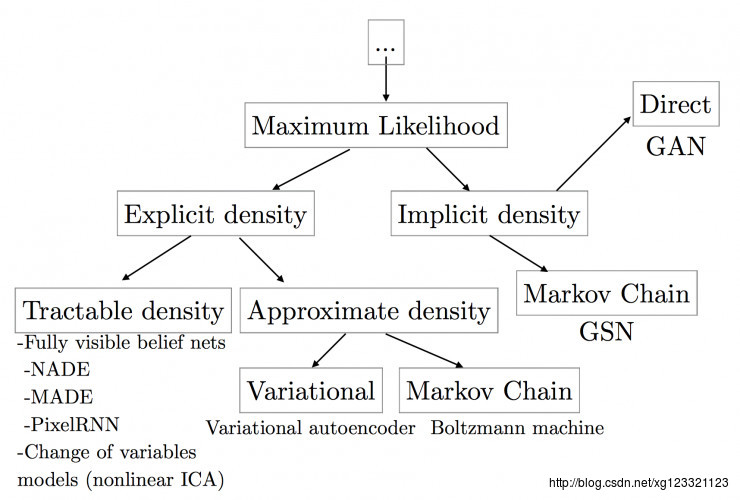
上图涵盖了基本的生成式模型的方法，主要按是否需要定义概率密度函数分为：

• Explicit density models
  这之中又分为tractable explicit models和approximate explicit model，tractable explicit model通常可以直接通过数学方法来建模求解，而approximate explicit model通常无法直接对数据分布进行建模，可以利用数学里的一些近似方法来做数据建模， 通常基于approximate explicit model分为确定性(变分方法：如VAE的lower bound)和随机性的方法(马尔科夫链蒙特卡洛方法, MCMC)。

• Implicit density models
  无需定义明确的概率密度函数，代表方法包括马尔科夫链、生成对抗式网络，该系列方法无需定义数据分布的描述函数。

• GAN能够有效地解决很多生成式方法的缺点，主要包括：

  • 并行产生samples；
  • 生成式函数的限制少，比如无需合适马尔科夫采样的数据分布（Boltzmann machines），生成式函数无需可逆、latent code无需与sample同维度（nonlinear ICA）；
  • 无需马尔科夫链的方法（Boltzmann machines， GSNs）；
  • 相对于VAE的方法，无需variational bound；
  • GAN比其他方法一般来说性能更好。

1 基本思想

GAN 的核心思想源于博弈论的纳什均衡。

设定参与游戏的双方分别为一个生成器(Generator)和一个判别器(Discriminator), 生成器捕捉真实数据样本的潜在分布, 并生成新的数据样本; 判别器是一个二分类器, 判别输入是真实数据还是生成的样本。
为了取得游戏胜利, 这两个游戏参与者需要不断优化, 各自提高自己的生成能力和判别能力, 这个学习优化过程就是寻找二者之间的一个纳什均衡。

GAN是一种二人零和博弈思想(two-player game)，博弈双方的利益之和是一个常数。

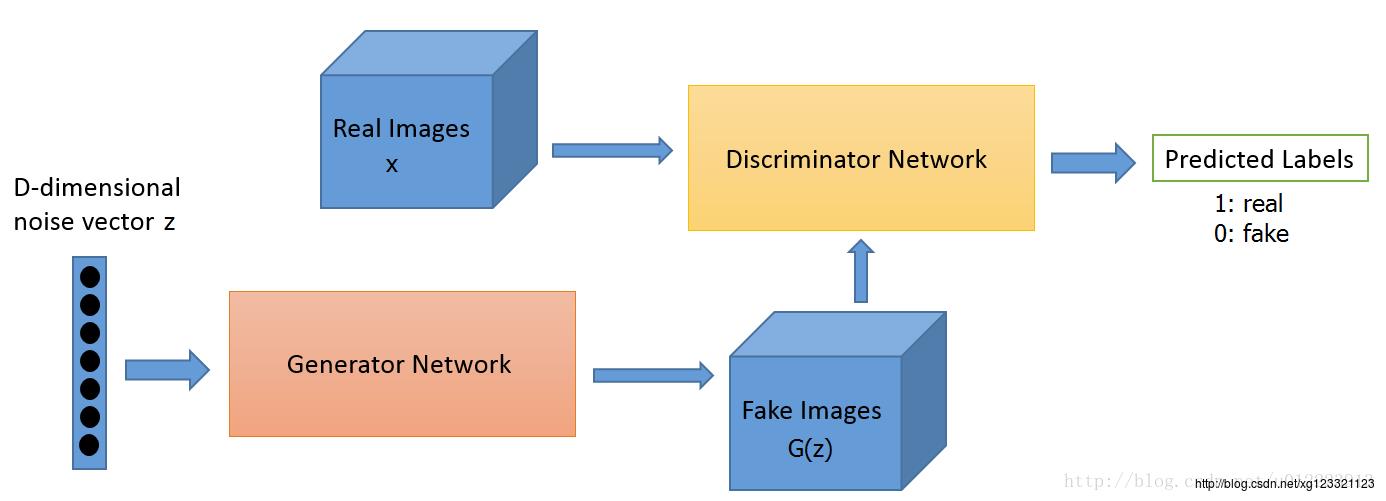
GAN的计算流程与结构如上图所示。

其中的生成器和判别器可以用任意可微分的函数, 这里我们用可微分函数D 和G 来分别表示判别器和生成器, 它们的输入分别为真实数据x 和随机变量z。
G(z) 为由G 生成的尽量服从真实数据分布$p_data$的样本。
如果判别器的输入来自真实数据, 标注为1.如果输入样本为G(z), 标注为0。

这里D 的目标是实现对数据来源的二分类判别: 真(来源于真实数据x 的分布) 或者伪(来源于生成器的伪数据G(z))。
而G 的目标是使自己生成的伪数据G(z) 在D 上的表现D(G(z)) 和真实数据x 在D 上的表现D(x)一致。

这是一个图片栗子：

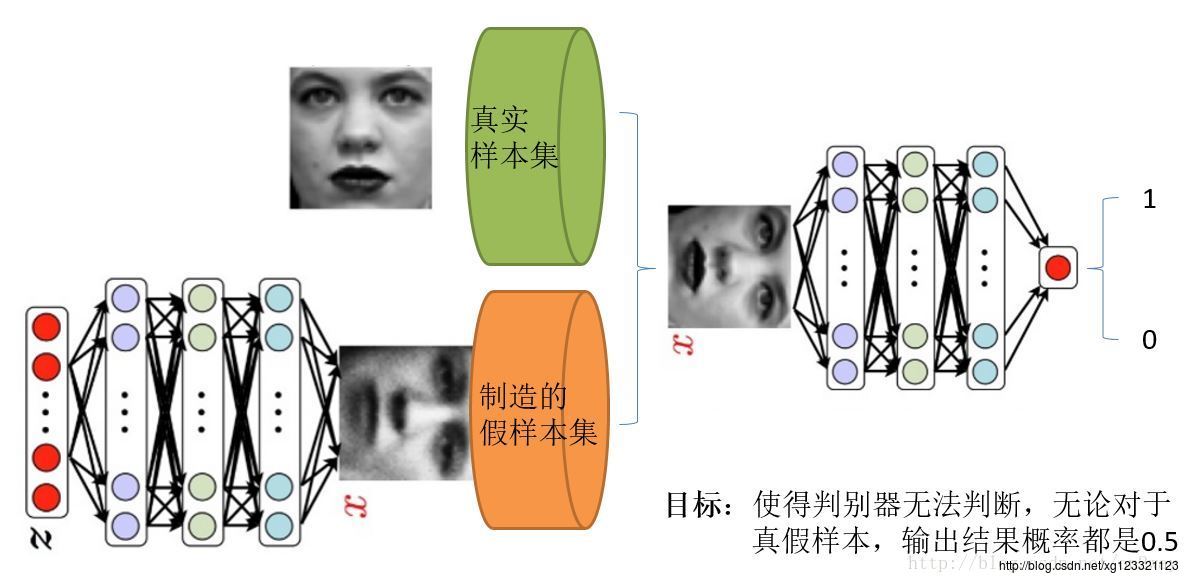
生成器和判别器都采用神经网络。

这个栗子中，我们有的只是真实采集而来的人脸样本数据集，值得一提的是我们连人脸数据集的类标签都没有，也就是我们不知道那个人脸对应的是谁。

最原始的GAN目的是想通过输入一个噪声，模拟得到一个人脸图像，这个图像可以非常逼真以至于以假乱真。(不同的任务想得到的东西不一样)

上图右半部分的判别模型，是一个简单的神经网络结构，输入一幅图像，输出是一个概率值，用于判断真假使用（概率值大于0.5那就是真，小于0.5那就是假，人们定义的概率）
左半部分的生成模型也是神经网络结构，输入是一组随机数Z，输出是一个图像，不再是一个数值。

从图中可以看到，会存在两个数据集，一个是真实数据集，另一个是假的数据集，由生成网络生成的数据集。

判别模型的目的：能判别出来属于的一张图它是来自真实样本集还是假样本集。假如输入的是真样本，网络输出就接近1，输入的是假样本，网络输出接近0。
生成网络的目的：使得自己生成样本的能力尽可能强，强到判别网络没法判断自己生成的样本是真还是假。

由此可见，生成模型与判别模型的目的正好相反，一个说我能判别得好，一个说我让你判别不好，所以叫做对抗，叫做博弈。

而最后的结果到底是谁赢，就要归结于模型设计者希望谁赢了。作为设计者的我们，如果是要得到以假乱真的样本，那么就希望生成模型赢，希望生成的样本很真，判别模型能力不足以区分真假样本。

2 训练过程

• 在噪声数据分布中随机采样，输入生成模型，得到一组假数据，记为$D(z)$；
• 在真实数据分布中随机采样，作为真实数据，记做$x$；
• 将前两步中某一步产生的数据作为判别网络的输入（因此判别模型的输入为两类数据，真/假），判别网络的输出值为该输入属于真实数据的概率，real为1，fake为0.
• 然后根据得到的概率值计算损失函数；
• 根据判别模型和生成模型的损失函数，可以利用反向传播算法，更新模型的参数。（先更新判别模型的参数，然后通过再采样得到的噪声数据更新生成器的参数）

还是以前面那张图为栗子：

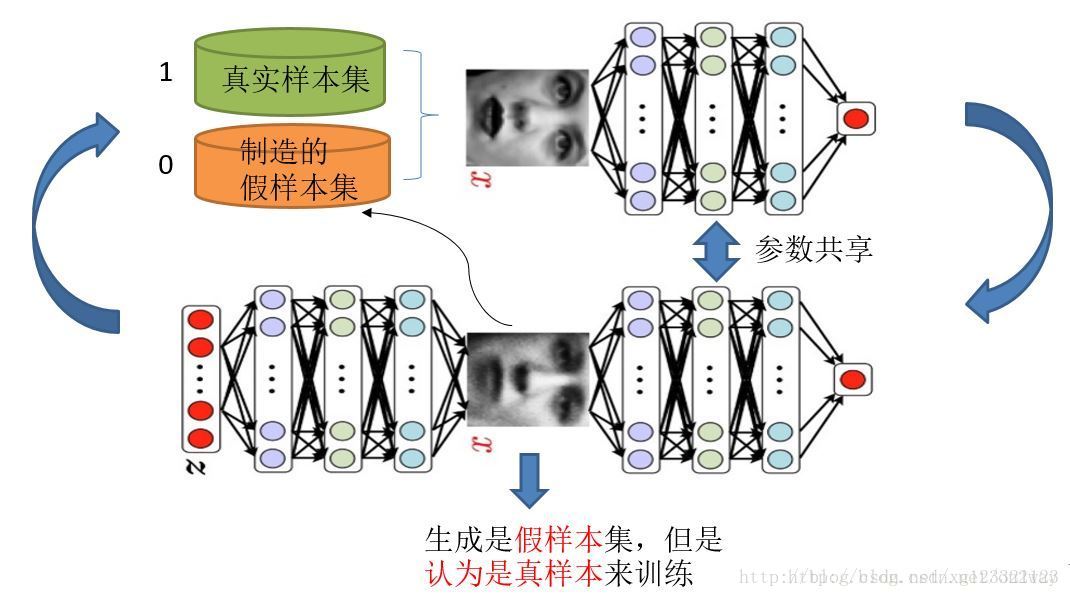
这里需要注意的是：生成模型与对抗模型是完全独立的两个模型，他们之间没有什么联系。那么训练采用的大原则是单独交替迭代训练。

因为是2个网络，不方便一起训练，所以才交替迭代训练。

• 先是判别网络：

  • 假设现在有了生成网络（当然可能不是最好的），那么给一堆随机数组，就会得到一堆假的样本集（因为不是最终的生成模型，现在生成网络可能处于劣势，导致生成的样本不太好，很容易就被判别网络判别为假）。

  • 现在有了这个假样本集(真样本集一直都有)，我们再人为地定义真假样本集的标签，很明显，这里我们默认真样本集的类标签为1，而假样本集的类标签为0，因为我们希望真样本集的输出尽可能为1，假样本集为0。

  • 现在有了真样本集以及它们的label(都是1)、假样本集以及它们的label(都是0)。这样一来，单就判别网络来说，问题变成了有监督的二分类问题了，直接送进神经网络中训练就好。

  • 判别网络训练完了。

• 继续来看生成网络：

  • 对于生成网络，我们的目的是生成尽可能逼真的样本。

  • 而原始的生成网络生成的样本的真实程度只能通过判别网络才知道，所以在训练生成网络时，需要联合判别网络才能达到训练的目的。

  • 所以生成网络的训练其实是对生成-判别网络串接的训练，像上图显示的那样。因为如果只使用生成网络，那么无法得到误差，也就无法训练。

  • 当通过原始的噪声数组Z生成了假样本后，把这些假样本的标签都设置为1，即认为这些假样本在生成网络训练的时候是真样本。因为此时是通过判别器来生成误差的，而误差回传的目的是使得生成器生成的假样本逐渐逼近为真样本(当假样本不真实，标签却为1时，判别器给出的误差会很大，这就迫使生成器进行很大的调整；反之，当假样本足够真实，标签为1时，判别器给出的误差就会减小，这就完成了假样本向真样本逐渐逼近的过程)，起到迷惑判别器的目的。

  • 现在对于生成网络的训练，有了样本集（只有假样本集，没有真样本集），有了对应的label（全为1），有了误差，就可以开始训练了。

  • 在训练这个串接网络时，一个很重要的操作是固定判别网络的参数，不让判别网络参数更新，只是让判别网络将误差传到生成网络，更新生成网络的参数。

• 在生成网络训练完后，可以根据用新的生成网络对先前的噪声Z生成新的假样本了，不出意外，这次生成的假样本会更真实。

• 有了新的真假样本集（其实是新的假样本集），就又可以重复上述过程了。

• 整个过程就叫单独交替训练。可以定义一个迭代次数，交替迭代到一定次数后停止即可。不出意外，这时噪声Z生成的假样本就会很真实了。

GAN设计的巧妙处之一，在于假样本在训练过程中的真假变换，这也是博弈得以进行的关键之处。

3 目标函数

上面提到，我们想要将一个随机高斯噪声z通过一个生成网络G得到一个和真的数据分布$P_data(x)$差不多的生成分布$P_G(x;\\theta)$,其中的参数$θ$是网络的参数决定的，我们希望找到 $θ$ 使得 $P_G(x;θ)$ 和 $P_data(x)$ 尽可能接近。

我们从真实数据分布 $P_data(x)$ 中取样m个点，$x^1,x^2,⋯,x^m$ ，根据给定的参数 $θ$ 我们可以计算如下的概率 $P_G(x^i;θ)$ ，那么生成这m个样本数据的似然(likelihood)就是

$$L=\\prod _i=1^mP_G(x^i;θ)$$

我们要做的就是找到 θ^∗ 来最大化这个似然估计(关于最大似然估计，可见我这篇博客)

$$θ^∗=arg\\space \\max_θ\\prod_i=1^mp_G(x^i;θ)⇔arg\\space \\max_θlog\\prod_i=1^mP_G(x^i;θ)$$
$$=arg\\space \\max_θ\\sum_i^mlogP_G(x^i;θ)$$
≈arg maxθEx∼Pdata[logPG(利用tensorflow训练简单的生成对抗网络GAN

GAN (生成对抗网络) 手写数字图片生成

不要怂，就是GAN (生成式对抗网络)

深度学习 GAN生成对抗网络-1010格式数据生成简单案例

GAN1-对抗神经网络梳理（GAN,WGAN,WGAN-GP）

不要怂 就是"干"如何用 TensorFlow 实现生成式对抗网络(GAN)