Java数据结构与算法解析——伸展树

Posted 2022-12-01 4K_WarCraft

伸展树简介

伸展树(Splay Tree)是特殊的二叉查找树。 
它的特殊是指，它除了本身是棵二叉查找树之外，它还具备一个特点: 当某个节点被访问时，伸展树会通过旋转使该节点成为树根。这样做的好处是，下次要访问该节点时，能够迅速的访问到该节点。

特性

1.和普通的二叉查找树相比，具有任何情况下、任何操作的平摊O(log2n)的复杂度，时间性能上更好 
2.和一般的平衡二叉树比如 红黑树、AVL树相比，维护更少的节点额外信息，空间性能更优，同时编程复杂度更低 
3.在很多情况下，对于查找操作，后面的查询和之前的查询有很大的相关性。这样每次查询操作将被查到的节点旋转到树的根节点位置，这样下次查询操作可以很快的完成 
4.可以完成对区间的查询、修改、删除等操作，可以实现线段树和树状数组的所有功能

旋转

伸展树实现O(log2n)量级的平摊复杂度依靠每次对伸展树进行查询、修改、删除操作之后，都进行旋转操作 Splay(x, root)，该操作将节点x旋转到树的根部。 
伸展树的旋转有六种类型，如果去掉镜像的重复，则为三种：zig(zag)、zig-zig(zag-zag)、zig-zag(zag-zig)。

1 自底向上的方式进行旋转

1.1 zig旋转 

如图所示，x节点的父节点为y，x为y的左子节点，且y节点为根。则只需要对x节点进行一次右旋(zig操作)，使之成为y的父节点，就可以使x成为伸展树的根节点。

1.2 zig-zig旋转 

如上图所示，x节点的父节点y，y的父节点z，三者在一字型链上。此时，先对y节点和z节点进行zig旋转，然后再对x节点和y节点进行zig旋转，最后变为右图所示，x成为y和z的祖先节点。

1.3 zig-zag旋转 

如上图所示，x节点的父节点y，y的父节点z，三者在之字型链上。此时，先对x节点和y节点进行zig旋转，然后再对x节点和y节点进行zag旋转，最后变为右图所示，x成为y和z的祖先节点。

2 自顶向下的方式进行旋转 
这种方式不需要节点存储其父节点的引用。当我们沿着树向下搜索某个节点x时，将搜索路径上的节点及其子树移走。构建两棵临时的树——左树和右树。没有被移走的节点构成的树称为中树。

(1) 当前节点x是中树的根 
(2) 左树L保存小于x的节点 
(3) 右树R保存大于x的节点

开始时候，x是树T的根，左树L和右树R都为空。三种旋转操作： 
2.1 zig旋转 

如图所示，x节点的子节点y就是我们要找的节点，则只需要对y节点进行一次右旋(zig操作)，使之成为x的父节点，就可以使y成为伸展树的根节点。将y作为中树的根，同时，x节点移动到右树R中，显然右树上的节点都大于所要查找的节点。

2.2 zig-zig旋转 
 
如上图所示，x节点的左子节点y，y的左子节点z，三者在一字型链上，且要查找的节点位于z节点为根的子树中。此时，对x节点和y节点进行zig，然后对z和y进行zig，使z成为中树的根，同时将y及其子树挂载到右树R上。

2.3 zig-zag旋转

如上图所示，x节点的左子节点y，y的右子节点z，三者在之字型链上，且需要查找的元素位于以z为根的子树上。此时，先对x节点和y节点进行zig旋转，将x及其右子树挂载到右树R上，此时y成为中树的根节点；然后再对z节点和y节点进行zag旋转，使得z成为中树的根节点。

2.4 合并 

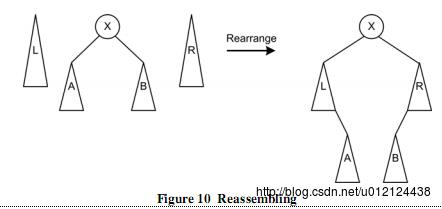
最后，找到节点或者遇到空节点之后，需要对左、中、右树进行合并。如图所示，将左树挂载到中树的最左下方（满足遍历顺序要求），将右树挂载到中树的最右下方（满足遍历顺序要求）。

伸展树的实现

1.节点

public class SplayTree<T extends Comparable<T>> 
    private SplayTreeNode<T> mRoot;    // 根结点

    public class SplayTreeNode<T extends Comparable<T>> 
        T key;                // 关键字(键值)
        SplayTreeNode<T> left;    // 左孩子
        SplayTreeNode<T> right;    // 右孩子

        public SplayTreeNode() 
            this.left = null;
            this.right = null;
        

        public SplayTreeNode(T key, SplayTreeNode<T> left, SplayTreeNode<T> right) 
            this.key = key;
            this.left = left;
            this.right = right;
        
    

 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

SplayTree是伸展树，而SplayTreeNode是伸展树节点。在此，我将SplayTreeNode定义为SplayTree的内部类。在伸展树SplayTree中包含了伸展树的根节点mRoot。SplayTreeNode包括的几个组成元素: 
(1) key – 是关键字，是用来对伸展树的节点进行排序的。 
(2) left – 是左孩子。 
(3) right – 是右孩子。

2.旋转

 /*
 * 旋转key对应的节点为根节点，并返回根节点。
 *
 * 注意：
 *   (a)：伸展树中存在"键值为key的节点"。
 *          将"键值为key的节点"旋转为根节点。
 *   (b)：伸展树中不存在"键值为key的节点"，并且key < tree.key。
 *      b-1 "键值为key的节点"的前驱节点存在的话，将"键值为key的节点"的前驱节点旋转为根节点。
 *      b-2 "键值为key的节点"的前驱节点存在的话，则意味着，key比树中任何键值都小，那么此时，将最小节点旋转为根节点。
 *   (c)：伸展树中不存在"键值为key的节点"，并且key > tree.key。
 *      c-1 "键值为key的节点"的后继节点存在的话，将"键值为key的节点"的后继节点旋转为根节点。
 *      c-2 "键值为key的节点"的后继节点不存在的话，则意味着，key比树中任何键值都大，那么此时，将最大节点旋转为根节点。
 */
    private SplayTreeNode<T> splay(SplayTreeNode<T> tree, T key) 
        if (tree == null)
            return tree;

        SplayTreeNode<T> N = new SplayTreeNode<T>();
        SplayTreeNode<T> l = N;
        SplayTreeNode<T> r = N;
        SplayTreeNode<T> c;

        for (; ; ) 
            int cmp = key.compareTo(tree.key);
            if (cmp < 0) 
                if (key.compareTo(tree.left.key) < 0) 
                    c = tree.left;                           /* rotate right */
                    tree.left = c.right;
                    c.right = tree;
                    tree = c;
                    if (tree.left == null)
                        break;
                
                r.left = tree;                               /* link right */
                r = tree;
                tree = tree.left;
             else if (cmp > 0) 

                if (tree.right == null)
                    break;

                if (key.compareTo(tree.right.key) > 0) 
                    c = tree.right;                          /* rotate left */
                    tree.right = c.left;
                    c.left = tree;
                    tree = c;
                    if (tree.right == null)
                        break;
                

                l.right = tree;                              /* link left */
                l = tree;
                tree = tree.right;
             else 
                break;
            
        
        l.right = tree.left;                                /* assemble */
        r.left = tree.right;
        tree.left = N.right;
        tree.right = N.left;

        return tree;
    

    public void splay(T key) 
        mRoot = splay(mRoot, key);
    


 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

上面的代码的作用：将”键值为key的节点”旋转为根节点，并返回根节点。它的处理情况共包括： 
(a)：伸展树中存在”键值为key的节点”。 
将”键值为key的节点”旋转为根节点。 
(b)：伸展树中不存在”键值为key的节点”，并且key < tree->key。 
b-1) “键值为key的节点”的前驱节点存在的话，将”键值为key的节点”的前驱节点旋转为根节点。 
b-2) “键值为key的节点”的前驱节点存在的话，则意味着，key比树中任何键值都小，那么此时，将最小节点旋转为根节点。 
(c)：伸展树中不存在”键值为key的节点”，并且key > tree->key。 
c-1) “键值为key的节点”的后继节点存在的话，将”键值为key的节点”的后继节点旋转为根节点。 
c-2) “键值为key的节点”的后继节点不存在的话，则意味着，key比树中任何键值都大，那么此时，将最大节点旋转为根节点。

下面列举个例子分别对a进行说明。 
在下面的伸展树中查找10，，共包括”右旋” –> “右链接” –> “组合”这3步。

01, 右旋 
对应代码中的”rotate right”部分 

02, 右链接 
对应代码中的”link right”部分 

03.组合 
对应代码中的”assemble”部分 

提示：如果在上面的伸展树中查找”70”，则正好与”示例1”对称，而对应的操作则分别是”rotate left”, “link left”和”assemble”。 
其它的情况，例如”查找15是b-1的情况，查找5是b-2的情况”等等，这些都比较简单，大家可以自己分析。

3.插入

/**
     * 将结点插入到伸展树中，并返回根节点
     * @param tree 伸展树的根节点
     * @param z 插入的结点
     * @return
     */
    private SplayTreeNode<T> insert(SplayTreeNode<T> tree, SplayTreeNode<T> z) 
        int cmp;
        SplayTreeNode<T> y = null;
        SplayTreeNode<T> x = tree;

        // 查找z的插入位置
        while (x != null) 
            y = x;
            cmp = z.key.compareTo(x.key);
            if (cmp < 0)
                x = x.left;
            else if (cmp > 0)
                x = x.right;
            else 
                System.out.printf("不允许插入相同节点(%d)!\\n", z.key);
                z = null;
                return tree;
            
        

        if (y == null)
            tree = z;
        else 
            cmp = z.key.compareTo(y.key);
            if (cmp < 0)
                y.left = z;
            else
                y.right = z;
        

        return tree;
    

    public void insert(T key) 
        SplayTreeNode<T> z = new SplayTreeNode<T>(key, null, null);

        // 如果新建结点失败，则返回。
        if ((z = new SplayTreeNode<T>(key, null, null)) == null)
            return;

        // 插入节点
        mRoot = insert(mRoot, z);
        // 将节点(key)旋转为根节点
        mRoot = splay(mRoot, key);
    
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

insert(key)是提供给外部的接口，它的作用是新建节点(节点的键值为key)，并将节点插入到伸展树中；然后，将该节点旋转为根节点。 
insert(tree, z)是内部接口，它的作用是将节点z插入到tree中。insert(tree, z)在将z插入到tree中时，仅仅只将tree当作是一棵二叉查找树，而且不允许插入相同节点。

4.删除

/**
     * 
     * @param tree 伸展树
     * @param key 删除的结点
     * @return
     */
    private SplayTreeNode<T> remove(SplayTreeNode<T> tree, T key) 
        SplayTreeNode<T> x;

        if (tree == null)
            return null;

        // 查找键值为key的节点，找不到的话直接返回。
        if (search(tree, key) == null)
            return tree;

        // 将key对应的节点旋转为根节点。
        tree = splay(tree, key);

        if (tree.left != null) 
            // 将"tree的前驱节点"旋转为根节点
            x = splay(tree.left, key);
            // 移除tree节点
            x.right = tree.right;
        
        else
            x = tree.right;

        tree = null;

        return x;
    

    public void remove(T key) 
        mRoot = remove(mRoot, key);
    
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

remove(key)是外部接口，remove(tree, key)是内部接口。 
remove(tree, key)的作用是：删除伸展树中键值为key的节点。 
它会先在伸展树中查找键值为key的节点。若没有找到的话，则直接返回。若找到的话，则将该节点旋转为根节点，然后再删除该节点。

伸展树实现完整代码

public class SplayTree<T extends Comparable<T>> 
    private SplayTreeNode<T> mRoot;    // 根结点

    public class SplayTreeNode<T extends Comparable<T>> 
        T key;                // 关键字(键值)
        SplayTreeNode<T> left;    // 左孩子
        SplayTreeNode<T> right;    // 右孩子

        public SplayTreeNode() 
            this.left = null;
            this.right = null;
        

        public SplayTreeNode(T key, SplayTreeNode<T> left, SplayTreeNode<T> right) 
            this.key = key;
            this.left = left;
            this.right = right;
        
    

    /*
 * 旋转key对应的节点为根节点，并返回根节点。
 *
 * 注意：
 *   (a)：伸展树中存在"键值为key的节点"。
 *          将"键值为key的节点"旋转为根节点。
 *   (b)：伸展树中不存在"键值为key的节点"，并且key < tree.key。
 *      b-1 "键值为key的节点"的前驱节点存在的话，将"键值为key的节点"的前驱节点旋转为根节点。
 *      b-2 "键值为key的节点"的前驱节点存在的话，则意味着，key比树中任何键值都小，那么此时，将最小节点旋转为根节点。
 *   (c)：伸展树中不存在"键值为key的节点"，并且key > tree.key。
 *      c-1 "键值为key的节点"的后继节点存在的话，将"键值为key的节点"的后继节点旋转为根节点。
 *      c-2 "键值为key的节点"的后继节点不存在的话，则意味着，key比树中任何键值都大，那么此时，将最大节点旋转为根节点。
 */
    private SplayTreeNode<T> splay(SplayTreeNode<T> tree, T key) 
        if (tree == null)
            return tree;

        SplayTreeNode<T> N = new SplayTreeNode<T>();
        SplayTreeNode<T> l = N;
        SplayTreeNode<T> r = N;
        SplayTreeNode<T> c;

        Java数据结构与算法解析——二叉查找树

 数据结构与算法问题 二叉搜索树
 Java数据结构和算法树
 D13-平衡二叉树[Java数据结构和算法]
 关于树论伸展树
 伸展树（Splay）详解