动态规划：动态规划的三种形式

Posted 2022-12-01 sun897949163

例：数字三角形（POJ 1163）

Language:Default The Triangle

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 45053		Accepted: 27208

Description

7
3   8
8   1   0
2   7   4   4
4   5   2   6   5

(Figure 1)

Figure 1 shows a number triangle. Write a program that calculates the highest sum of numbers passed on a route that starts at the top and ends somewhere on the base. Each step can go either diagonally down to the left or diagonally down to the right.

Input

Your program is to read from standard input. The first line contains one integer N: the number of rows in the triangle. The following N lines describe the data of the triangle. The number of rows in the triangle is > 1 but <= 100. The numbers in the triangle, all integers, are between 0 and 99.

Output

Your program is to write to standard output. The highest sum is written as an integer.

Sample Input

5
7
3 8
8 1 0 
2 7 4 4
4 5 2 6 5

Sample Output

30

Source

IOI 1994

基本思路

用二维数组存放数字三角形。

D( r, j) : 第r行第 j 个数字(r,j从1开始算)
MaxSum(r, j) : 从D(r,j)到底边的各条路径中，
最佳路径的数字之和。
问题：求 MaxSum(1,1)

典型的递归问题。
D(r, j)出发，下一步只能走D(r+1,j)或者D(r+1, j+1)。故对于N行的三角形：

if ( r == N)
    MaxSum(r,j) = D(r,j)
else
    MaxSum( r, j) = Max MaxSum(r＋1,j), MaxSum(r+1,j+1)  + D(r,j)

然后你会发现：

为什么超时

重复计算

如果采用递规的方法，深度遍历每条路径，存在大量重复计算。则时间复杂度为 2n,对于 n = 100 行，肯定超时。

改进

如果每算出一个MaxSum(r,j)就保存起来，下次用到其值的时候直接取用，则可免去重复计算。那么可以用O(n2)时间完成计算。因为三角形的数字总数是 n(n+1)/2

改进代码

#include <iostream>
#include <algorithm>
#define MAX 101
using namespace std;

int D[MAX][MAX]; int n;
int maxSum[MAX][MAX];

int MaxSum(int i, int j)
 
    if (maxSum[i][j] != -1)
        return maxSum[i][j];
    if (i == n) maxSum[i][j] = D[i][j];
    else 
        int x = MaxSum(i + 1, j);
        int y = MaxSum(i + 1, j + 1);
        maxSum[i][j] = max(x, y) + D[i][j];
    
    return maxSum[i][j];


int main()
 
    int i, j; 
    cin >> n;
    for (i = 1; i <= n; i++)
        for (j = 1; j <= i; j++) 
         
            cin >> D[i][j]; 
            maxSum[i][j] = -1;
        
    cout << MaxSum(1, 1) << endl;

转化为递推

“人人为我”型递推

#include <iostream>
#include <algorithm>
#define MAX 101
using namespace std;

int D[MAX][MAX]; int n;
int maxSum[MAX][MAX];

int main()

    int i, j;
    cin >> n;
    for (i = 1; i <= n; i++)
        for (j = 1; j <= i; j++)
            cin >> D[i][j];
    for (int i = 1; i <= n; ++i)
        maxSum[n][i] = D[n][i];
    for (int i = n - 1; i >= 1; --i)
        for (int j = 1; j <= i; ++j)
            maxSum[i][j] = max(maxSum[i + 1][j], maxSum[i + 1][j + 1]) + D[i][j];
            cout << maxSum[1][1] << endl;

这里说的人人为我型递归就是在求DP[i][j]的过程中， 使用DP[i-1][1]→DP[i - 1][i - 1]来推到出DP[i][j];

“我为人人”型递归

#include <iostream>
#include <algorithm>
#define MAX 101
using namespace std;

int D[MAX][MAX]; int n;
int maxSum[MAX][MAX];

int main()

    int i, j;
    cin >> n;
    for (i = 1; i <= n; i++)
        for (j = 1; j <= i; j++)
            cin >> maxSum[i][j];

    for (int i = 1; i < n; i++)
    
        for (int j = 1; j <= i; j++)
        
            maxSum[i + 1][j] = max(maxSum[i + 1][j], maxSum[i + 1][j] + maxSum[i][j]);
            maxSum[i + 1][j + 1] = max(maxSum[i + 1][j + 1], maxSum[i + 1][j + 1] + maxSum[i][j]);
        
    
    int maxx = -9999999999;
    for (int i = 1; i <= n; i++)
        maxx = max(maxx, maxSum[n][i]);
    cout << maxx << endl;

这里说的人人为我型递归就是在求DP[i][j]的过程中， 求出DP[i + 1][j]和DP[i + 1][j +1]的其中一个解。

空间优化

没必要用二维maxSum数组存储每一个MaxSum(r,j),只要从底层一行行向上递推，那么只要一维数组maxSum[100]即可,即只要存储一行的MaxSum值就可以。

进一步考虑，连maxSum数组都可以不要，直接用D的第n行替代maxSum即可。

节省空间，时间复杂度不变

#include <iostream>
#include <algorithm>
#define MAX 101
using namespace std;

int D[MAX][MAX];
int n; int * maxSum;

int main() 

    int i, j;
    cin >> n;
    for (i = 1; i <= n; i++)
        for (j = 1; j <= i; j++)
            cin >> D[i][j];
    maxSum = D[n]; //maxSum指向第n行
    for (int i = n - 1; i >= 1; --i)
        for (int j = 1; j <= i; ++j)
            maxSum[j] = max(maxSum[j], maxSum[j + 1]) + D[i][j];
    cout << maxSum[1] << endl;

·
·
·

总结三种动态规划的形式

人人为我

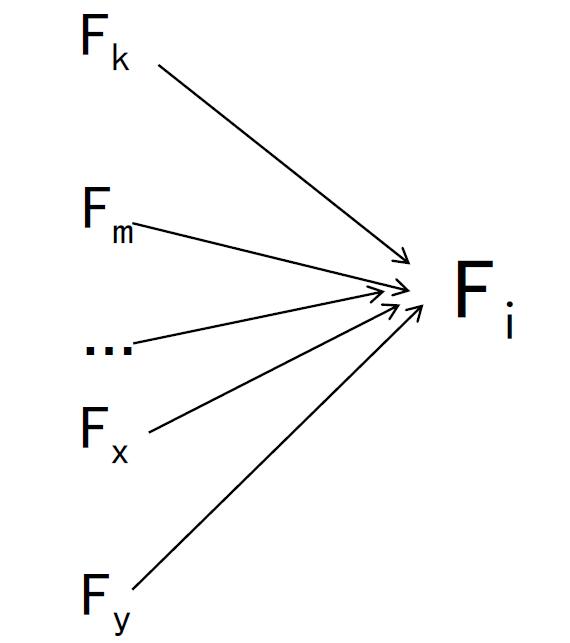
状态i的值Fi由若干个值已知的状态值Fk,Fm,..Fy推出，如求和，取最大值

我为人人

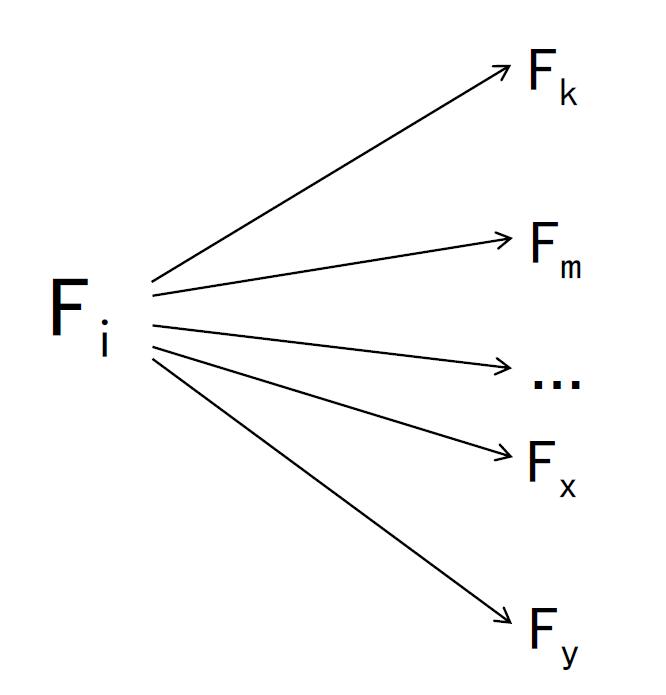
状态i的值Fi在被更新（不一定是最终求出）的时候，依据Fi去更新（不一定是最终求出）和状态i相关的其他一些状态的值Fk,Fm,..Fy

注意：在选取最优备选状态的值Fm,Fn,…Fy时，有可能有好的算法或数据结构可以用来显著降低时间复杂度。

记忆型递归

优点：只经过有用的状态，没有浪费。递推型会查看一些没用的状态，有浪费

缺点：可能会因递归层数太深导致爆栈，函数调用带来额外时间开销。无法使用滚动数组节省空间。总体来说，比递推型慢。