机器学习多标签分类的评价指标与代码实现

Posted 2022-12-01 征途黯然.

[1] 总览

  6个基本评价指标如下思维导图：

[2] 介绍

  假设有数据：样本数batch_size = 5，标签数label_num = 4。y_true为真实标签，y_pred为预测标签值。

y_true = np.array([[0, 1, 0, 1],
                   [0, 1, 1, 0],
                   [0, 0, 1, 0],
                   [1, 1, 1, 0],
                   [1, 0, 1, 1]])

y_pred = np.array([[0, 1, 1, 0],
                   [0, 1, 1, 0],
                   [0, 0, 1, 0],
                   [0, 1, 1, 0],
                   [0, 1, 0, 1]])

[2.1] 子集准确率（Subset Accuracy）

  对于每一个样本来说，只有预测值与真实值完全相同的情况下才算预测正确，也就是说只要有一个类别的预测结果有差异都算没有预测正确。因此，其计算公式为：

  对照上面给的数据y_true、y_pred。那么只有第2个和第3个样本才算预测正确。在sklearn中，可以直接通过sklearn.metrics模块中的accuracy_score方法来完成计算[3]，代码实现：

from sklearn.metrics import accuracy_score

print(accuracy_score(y_true,y_pred)) # 0.4

print(accuracy_score(y_true,y_pred,normalize=False)) # 2

【注】
accuracy_score有参数normalize。
normalize = False时：返回完全正确的样本数，
normalize = True时：返回完全正确的样本数的占比。

[2.2] 准确率（Accuracy）

  准确率计算的是所有样本的平均准确率。而对于每个样本来说，准确率就是预测正确的标签数在整个预测为正确或真实为正确标签数中的占比。其计算公式为：

  例如对于某个样本来说，其真实标签为[0, 1, 0, 1]，预测标签为[0, 1, 1, 0]。那么该样本对应的准确率就应该为：（0 + 1 + 0 + 0） / （0 + 1 + 1 + 1）= 0.33。

  对照上面给的数据y_true、y_pred。那么该样本对应的准确率就应该为：
$$\frac{1}{5}\ast (\frac{1}{3}+\frac{2}{2}+\frac{1}{1}+\frac{2}{3}+\frac{1}{4})=0.65$$

  在sklearn中，acc只有子集准确率，所以此处我们要自己实现。代码实现：

def Accuracy(y_true, y_pred):
    count = 0
    for i in range(y_true.shape[0]):
        p = sum(np.logical_and(y_true[i], y_pred[i]))
        q = sum(np.logical_or(y_true[i], y_pred[i]))
        count += p / q
    return count / y_true.shape[0]
    
print(Accuracy(y_true, y_pred)) # 0.65

[2.3] 精确率（Precision）

  精确率计算的是所有样本的平均精确率。而对于每个样本来说，精确率就是预测正确的标签数在整个预测为正确的标签数中的占比。其计算公式为：

  例如对于某个样本来说，其真实标签为[0, 1, 0, 1]，预测标签为[0, 1, 1, 0]。那么该样本对应的精确率就应该为：（0 + 1 + 0 + 0） / （1 + 1）= 0.5。

  对照上面给的数据y_true、y_pred。那么该样本对应的准确率就应该为：
$$\frac{1}{5}\ast (\frac{1}{2}+\frac{2}{2}+\frac{1}{1}+\frac{2}{2}+\frac{1}{2})=0.8$$

  代码实现：

from sklearn.metrics import precision_score

print(precision_score(y_true=y_true, y_pred=y_pred, average='samples'))# 0.8

[2.4] 召回率（Recall）

  召回率其实计算的是所有样本的平均召回率。而对于每个样本来说，召回率就是预测正确的标签数在整个正确的标签数中的占比。其计算公式为：

  例如对于某个样本来说，其真实标签为[0, 1, 0, 1]，预测标签为[0, 1, 1, 0]。那么该样本对应的精确率就应该为：（0 + 1 + 0 + 0） / （1 + 1）= 0.5。

  对照上面给的数据y_true、y_pred。那么该样本对应的准确率就应该为：
$$\frac{1}{5}\ast (\frac{1}{2}+\frac{2}{2}+\frac{1}{1}+\frac{2}{3}+\frac{1}{3})=0.7$$

  代码实现：

from sklearn.metrics import recall_score

print(recall_score(y_true=y_true, y_pred=y_pred, average='samples'))# 0.7

[2.5] F1

  其计算公式为：

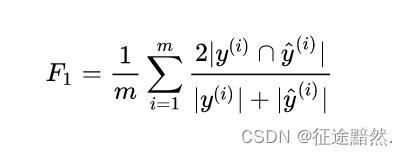
  例如对于某个样本来说，其真实标签为[0, 1, 0, 1]，预测标签为[0, 1, 1, 0]。那么该样本对应的精确率就应该为：2 * （0 + 1 + 0 + 0） / （（1 + 1）+（1 + 1））= 0.5。

  对照上面给的数据y_true、y_pred。那么该样本对应的准确率就应该为：
$$2\ast \frac{1}{5}\ast (\frac{1}{4}+\frac{2}{4}+\frac{1}{2}+\frac{2}{5}+\frac{1}{5})=0.74$$

  代码实现：

from sklearn.metrics import f1_score

print(f1_score(y_true,y_pred,average='samples'))# 0.74

[2.6] 汉明损失（Hamming Loss）

  Hamming Loss衡量的是所有样本中，预测错的标签数在整个标签标签数中的占比。所以对于Hamming Loss损失来说，其值越小表示模型的表现结果越好。
  对照上面给的数据y_true、y_pred。那么该样本对应的准确率就应该为：
$$\frac{1}{5\ast 4}\ast (2+0+0+1+3)=0.3$$

  代码实现：

from sklearn.metrics import hamming_loss
print(hamming_loss(y_true, y_pred))# 0.3