g2o中 EdgeSE3Expmap类型Jacobian的计算

Posted 2022-11-30 白巧克力亦唯心

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了g2o中 EdgeSE3Expmap类型Jacobian的计算相关的知识，希望对你有一定的参考价值。

位姿优化的时候，两个顶点的类型是SE3，涉及到的误差雅克比是pose error对pose的求导，里面有些知识值得注意，故记录下来。

前期准备

重新翻看Ethan Eade的《Lie Groups for 2D and 3D Transformations》，发现他的文档早已有相关推导。比如针对两个SO3乘积对其中一个求导：

比如同理两个SE3乘积, 对其中一个求导：

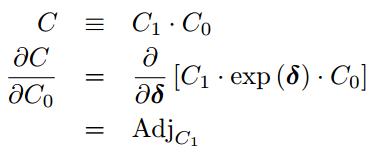
上面这两个推导都利用了adjoint的性质。这部分Ethan Eade的文档中有，也可参看strasdat phd thesis 2.4.7部分的定义：

exp([adjT⋅ξ]×)=Texp(ξ^)T−1 $\\exp([adj_T\\cdot\\xi]_\\times)=T\\exp(\\hat\\xi)T^-1$
由上面的公式可以简单得到如下性质，这个性质要牢记，预积分里反复用到了:

Texp(ξ^)=Texp(ξ^)T−1T=exp([adjT⋅ξ]×)Texp(ξ^)T−1=T−1exp([adjT⋅ξ]×) $\\colorblueT\\exp(\\hat\\xi)=T\\exp(\\hat\\xi)T^-1T=\\exp([adj_T\\cdot\\xi]_\\times)T \\\\ \\colorblue\\exp(\\hat\\xi)T^-1=T^-1\\exp([adj_T\\cdot\\xi]_\\times)$
很容易看出，当

T $T$ 和

exp() $exp()$ 相乘时，利用这个性质可以调换它们的乘法位置，左乘变右乘，这在求导的时候十分有用。
稍加改变有：

exp(ξ^)T=Texp([adjT−1⋅ξ]×) $\\exp(\\hat\\xi)T=T\\exp([adj_T^-1\\cdot\\xi]_\\times)$
同时可以计算出

adjT $adj_T$ 的计算公式(Ethan Eade文档)：

EdgeSE3Expmap中雅克比推导

有了Ethan文档的雅克比推导，EdgeSE3Expmap中雅克比的计算依葫芦画瓢就行了。首先通过代码看图优化里位姿边的误差定义，types_six_dof_expmap.h 文件第118行:

    void computeError()  
      const VertexSE3Expmap* v1 = static_cast<const VertexSE3Expmap*>(_vertices[0]);
      const VertexSE3Expmap* v2 = static_cast<const VertexSE3Expmap*>(_vertices[1]);

      SE3Quat C(_measurement);
      SE3Quat error_= v2->estimate().inverse()*C*v1->estimate();
      _error = error_.log();

写成公式形式如下:

Terr=T−1jwT^jiTiw $T_err =T_jw^-1\\hatT_jiT_iw$
其中

T^ji $\\hatT_ji$ 表示位姿变换的测量。

上面误差公式是多个位姿相乘的形式，所以借鉴前面的推导过程，下面开始对误差的雅克比进行推导，先看下g2o代码的实现，types_six_dof_expmap.cpp 文件第274行，可以看到求得的导数也是某个位姿的adj()形式，所以验证了推导思路没错:

void EdgeSE3Expmap::linearizeOplus() 
  VertexSE3Expmap * vi = static_cast<VertexSE3Expmap *>(_vertices[0]);
  SE3Quat Ti(vi->estimate());

  VertexSE3Expmap * vj = static_cast<VertexSE3Expmap *>(_vertices[1]);
  SE3Quat Tj(vj->estimate());

//注意这里把测量标记为Tij应该是标记错误了，应该是Tji，不然整个误差公式说不通了
//这个可以看orbslam EdgeSim3里添加测量时就是用的Sji
  const SE3Quat & Tij = _measurement;　　　// shoulb be Tji
  SE3Quat invTij = Tij.inverse();

  SE3Quat invTj_Tij = Tj.inverse()*Tij;
  SE3Quat infTi_invTij = Ti.inverse()*invTij;

  _jacobianOplusXi = invTj_Tij.adj();
  _jacobianOplusXj = -infTi_invTij.adj();

误差雅克比中误差对变量 $X_j$ (位姿j)的推导，也就是微小增量作用在位姿j上：

Terr=T−1jwT^jiTiwξerr=log(Terr)Terr(δξj′j)=(exp(δξj′jˆ)Tjw)−1Tubuntu上G2O库的安装

SLAM14讲 ch6 g2o曲线拟合程序问题