二叉树的遍历

Posted 2020-11-19 b02330224

二叉树的遍历

树的遍历是树的一种重要的运算。所谓遍历是指对树中所有结点的信息的访问，即依次对树中每个结点访问一次且仅访问一次，我们把这种对所有节点的访问称为遍历（traversal）。那么树的两种重要的遍历模式是深度优先遍历和广度优先遍历,深度优先一般用递归，广度优先一般用队列。一般情况下能用递归实现的算法大部分也能用堆栈来实现。

深度优先遍历

对于一颗二叉树，深度优先搜索(Depth First Search)是沿着树的深度遍历树的节点，尽可能深的搜索树的分支。
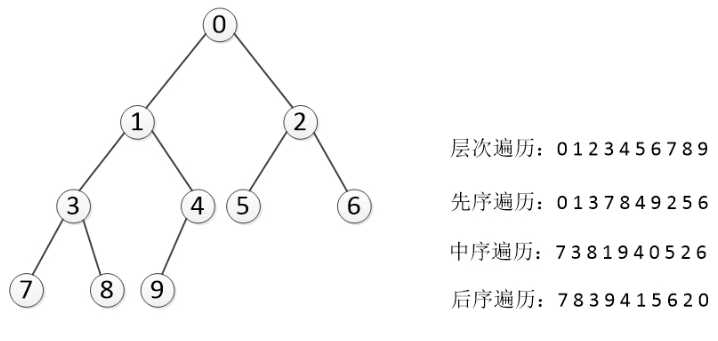
那么深度遍历有重要的三种方法。这三种方式常被用于访问树的节点，它们之间的不同在于访问每个节点的次序不同。这三种遍历分别叫做先序遍历（preorder），中序遍历（inorder）和后序遍历（postorder）。我们来给出它们的详细定义，然后举例看看它们的应用。

• 先序遍历 在先序遍历中，我们先访问根节点，然后递归使用先序遍历访问左子树，再递归使用先序遍历访问右子树
  根节点->左子树->右子树

• def preorder(self, root):
        """递归实现先序遍历"""
        if root == None:
            return
        print root.elem
        self.preorder(root.lchild)
        self.preorder(root.rchild)

   

• 中序遍历 在中序遍历中，我们递归使用中序遍历访问左子树，然后访问根节点，最后再递归使用中序遍历访问右子树
  左子树->根节点->右子树

  def inorder(self, root):
        """递归实现中序遍历"""
        if root == None:
            return
        self.inorder(root.lchild)
        print root.elem
        self.inorder(root.rchild)

   

• 后序遍历 在后序遍历中，我们先递归使用后序遍历访问左子树和右子树，最后访问根节点
  左子树->右子树->根节点

  def postorder(self, root):
        """递归实现后续遍历"""
        if root == None:
            return
        self.postorder(root.lchild)
        self.postorder(root.rchild)
        print root.elem

  

•  

  

•  

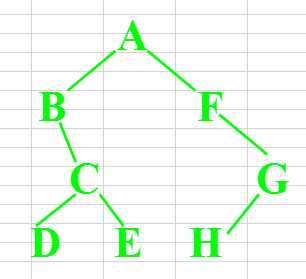
  广度优先遍历(层次遍历)

  从树的root开始，从上到下从从左到右遍历整个树的节点

  def breadth_travel(self, root):
          """利用队列实现树的层次遍历"""
          if root == None:
              return
          queue = []
          queue.append(root)
          while queue:
              node = queue.pop(0)
              print node.elem,
              if node.lchild != None:
                  queue.append(node.lchild)
              if node.rchild != None:
                  queue.append(node.rchild)

   python代码：

• class Node(object):
      """"""
      def __init__(self, item):
          self.elem = item
          self.lchild = None
          self.rchild = None
  
  class Tree(object):
      """二叉树"""
      def __init__(self):
          self.root = None
  
      def add(self, item):
          node = Node(item)
          if self.root is None:
              self.root = node
              return
          queue = [self.root]
          while queue:
              cur_node = queue.pop(0)
              if cur_node.lchild is None:
                  cur_node.lchild = node
                  return
              else:
                  queue.append(cur_node.lchild)
              if cur_node.rchild is None:
                  cur_node.rchild = node
                  return
              else:
                  queue.append(cur_node.rchild)
  
      def breadth_travel(self):
          """广度遍历"""
          if self.root is None:
              return
          queue = [self.root]
          while queue:
              cur_node = queue.pop(0)
              print(cur_node.elem, end=" ")
              if cur_node.lchild is not None:
                  queue.append(cur_node.lchild)
              if cur_node.rchild is not None:
                  queue.append(cur_node.rchild)
  
      def preorder(self, node):
          """先序遍历"""
          if node is None:
              return
          print(node.elem, end=" ")
          self.preorder(node.lchild)
          self.preorder(node.rchild)
  
      def inorder(self, node):
          """中序遍历"""
          if node is None:
              return
          self.inorder(node.lchild)
          print(node.elem, end=" ")
          self.inorder(node.rchild)
  
      def postorder(self, node):
          """后序遍历"""
          if node is None:
              return
          self.postorder(node.lchild)
          self.postorder(node.rchild)
          print(node.elem, end=" ")
  
  
  if __name__ == "__main__":
      tree = Tree()
      tree.add(0)
      tree.add(1)
      tree.add(2)
      tree.add(3)
      tree.add(4)
      tree.add(5)
      tree.add(6)
      tree.add(7)
      tree.add(8)
      tree.add(9)
      tree.breadth_travel()
      print(" ")
      tree.preorder(tree.root)
      print(" ")
      tree.inorder(tree.root)
      print(" ")
      tree.postorder(tree.root)
      print(" ")