Educational Codeforces Round 124 (Rated for Div. 2)(ABCD)

Posted 2022-11-29 斗奋力努

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Educational Codeforces Round 124 (Rated for Div. 2)(ABCD)相关的知识，希望对你有一定的参考价值。

Educational Codeforces Round 124 (Rated for Div. 2)(ABCD)

总结：日常犯病，细节处理不好
A. Playoff

题意：给定数字n，有 $2^n$ 个人进行比赛，按顺序排好，每次两两比赛，如果两者和相加为奇数，则数字较小的晋级；否则数字较大的晋级。
思路：根据样例盲猜答案是 $2^n-1$ ，幸运水过

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+5;
int n,m,q,a[N];

void solve()
    scanf("%d",&n);
    printf("%d\\n",(1<<n)-1);


int main()
    int T;scanf("%d",&T);
    while(T--) solve();
    return 0;

B. Prove Him Wrong
题意：给定数字n，问是否存在n个数字，保证每个数字的值为在区间 $[1, 1 e 9]$ ,且任意两个数字相减的绝对值*2要大于等于原来两个数的和
思路：肯定可以初始化一个最长可能序列，为了保证条件，发现当序列中每个数呈现3倍的关系就行了，初始数值为1

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+5;
int n,m,q,a[N];
vector<int>ans;

void solve()
    scanf("%d",&n);
    int len=ans.size();
    if(n>len) puts("NO");
    else
        puts("YES");
        for(int i=0;i<n;i++) printf("%d ",ans[i]);
        puts("");
    


int main()
    int now=1;
    while(now<=1e9)
        ans.push_back(now);
        now=now*3;
    
    int T;scanf("%d",&T);
    while(T--) solve();
    return 0;

C. Fault-tolerant Network
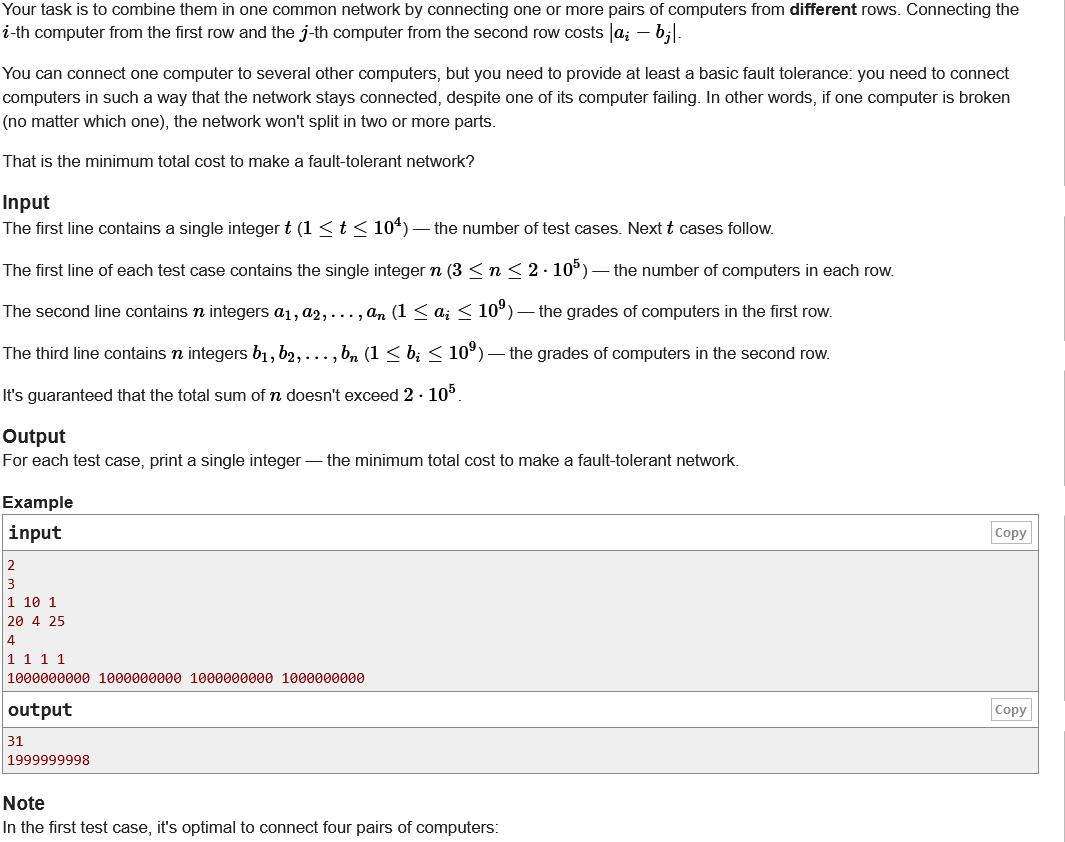题意：给定序列长度n，有上下两个序列a,b,每个序列的内部相邻的位置链接在一起，现在要新加一些边，保证无论删除两个序列中的哪一个位置，剩下的 $2 * n - 1$ 个数会在一个连通块内，新加一条a[i]到b[j]的边所需要花费为abs(a[i]-b[j])
思路：
我们很容易得到，当初始呈现”环形“时，一定满足条件，即 $a b s (a [1] - b [1]) + a b s (a [n] - b [n])$ 或 $a b s (a [1] - b [n]) + a b s (a [n] - b [1])$
同时发现：
如果选择 $a b s (a [1] - b [1])$ 我们也可以再加上一条端点包括 $a [n]$ 和一条端点包括 $b [n]$ 的两条边
如果选择 $a b s (a [n] - b [n])$ 我们也可以再加上一条端点包括 $a [1]$ 和一条端点包括 $b [3]$ 的两条边
如果选择 $a b s (a [1] - b [n])$ 我们也可以再加上一条端点包括 $a [n]$ 和一条端点包括 $b [1]$ 的两条边
如果选择 $a b s (a [n] - b [1])$ 我们也可以再加上一条端点包括 $a [1]$ 和一条端点包括 $b [n]$ 的两条边

总之：两个序列的四角位置的点都需要作为某条新边的端点就行了(口胡)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+5;
ll n,m,q,a[N],b[N];
ll mx[7];

void solve()
    scanf("%lld",&n);
    for(ll i=1;i<=n;i++) scanf("%lld",&a[i]);
    for(ll i=1;i<=n;i++) scanf("%lld",&b[i]);
    mx[0]=min(abs(a[1]-b[1])+abs(a[n]-b[n]),abs(a[1]-b[n])+abs(a[n]-b[1]));
    mx[1]=mx[2]=mx[3]=mx[4]=1e18;
    for(ll i=1;i<=n;i++)
        mx[1]=min(mx[1],abs(a[1]-b[i]));
        mx[2]=min(mx[2],abs(a[n]-b[i]));
        mx[3]=min(mx[3],abs(b[1]-a[i]));
        mx[4]=min(mx[4],abs(b[n]-a[i]));
    
    ll ans=min(mx[0],mx[1]+mx[2]+mx[3]+mx[4]);
    ans=min(ans,abs(a[1]-b[1])+mx[2]+mx[4]);
    ans=min(ans,abs(a[n]-b[n])+mx[1]+mx[3]);
    ans=min(ans,abs(a[1]-b[n])+mx[2]+mx[3]);
    ans=min(ans,abs(a[n]-b[1])+mx[1]+mx[4]);
    printf("%lld\\n",ans);


int main()
    int T;scanf("%d",&T);
    while(T--) solve();
    return 0;

D. Nearest Excluded Points
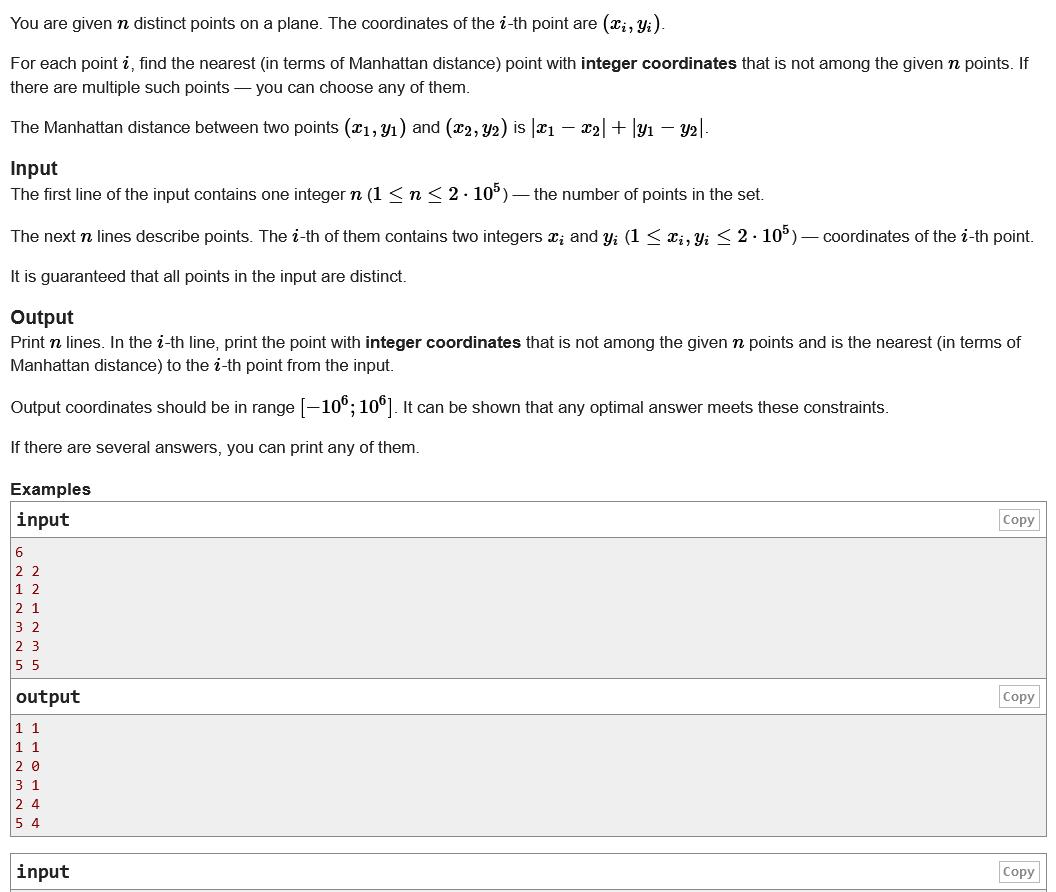题意：给定n个点，找出每个点的最短曼哈顿距离的点的坐标，这些坐标不能是初始n个点的坐标
思路：赶紧是最近cf的一种套路，来回讨论模拟(口胡)。
我们可以用两个queue。依次讨论每个queue，直到讨论是遇到queue为空截止。我们初始将四周有空地的点加入q1，随后讨论q1，遇到空地就直接记录答案，如果没有，则表示我们是最近到达四周点的坐标，我们的最短曼哈顿距离也就是四周点的最短曼哈顿距离+1，且该点的答案坐标也可就是四周已处理点的答案，否则将点给q2；q2同操作，可以保证最优解。
（具体可以看代码，来回讨论部分基本一样）

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+5;
int n,m;
struct nodeint x,y,id,cnt;pg[N],ans[N];
map<pair<int,int>,int>mp;//每个点的编号
bool vis[N];
queue<node>q1,q2;
int dx[]=-1,1,0,0;
int dy[]=0,0,-1,1;

void solve()
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        int x,y;scanf("%d%d",&x,&y);
        pg[i]=x,y,i;
        mp[x,y]=i;//每个点的编号
    
    for(int i=1;i<=n;i++)
        int num=0;
        for(int j=0;j<4;j++)
            int nx=pg[i].x+dx[j];
            int ny=pg[i].y+dy[j];
            if(mp.find(nx,ny)!=mp.end()) num++; //存在空地，num++
        
        if(num!=4) q1.push(pg[i].x,pg[i].y,pg[i].id,1);//不等于4代表四周一定有空地，初始加入q1，且最小曼哈顿距离为1
    
    int tag=1;
    while(1)
        if(tag==1)
            if(q1.size()==0) break;
            while(!q1.empty())
                auto u=q1.front(); q1.pop();
                if(vis[u.id]) continue;
                vis[u.id]=true;
                bool flag=false;
                int dis=1e9,idx=-1;
                for(int i=0;i<4;i++)//遍历四周的点P
                    int nx=u.x+dx[i];
                    int ny=u.y+dy[i];
                    if(mp.find(nx,ny)==mp.end())//点P空地，最近点就是点P，且最小曼哈顿距离为1
                        flag=true;//标记已经找到最优解
                        ans[u.id]=nx,ny,0,1;
                    
                    else
                        if(vis[mp[nx,ny]]&&dis>1+ans[mp[nx,ny]].cnt)//点P已经有最优解，且到点P的最优解的距离最小，idx记录方向
                            dis=1+ans[mp[nx,ny]].cnt;
                            idx=i;
                        
                        //点P还没有最优解，那么当该点有最优解后，点P的最小曼哈顿距离已经是该点的最优解
                        //所以是下一次讨论，即加入q2
                        else if(!vis[mp[nx,ny]]) q2.push(nx以上是关于Educational Codeforces Round 124 (Rated for Div. 2)(ABCD)的主要内容，如果未能解决你的问题，请参考以下文章 
 Educational Codeforces Round 7 A
 Educational Codeforces Round 7
 Educational Codeforces Round 90
 Educational Codeforces Round 33
 Codeforces Educational Codeforces Round 54 题解
 Educational Codeforces Round 27