从零开始实现主成分分析(PCA)算法

Posted 2022-11-28 风雪夜归子

声明：版权所有，转载请联系作者并注明出处:
http://blog.csdn.net/u013719780?viewmode=contents

知乎专栏：
https://www.zhihu.com/people/feng-xue-ye-gui-zi

前面两篇文章详细讲解了线性判别分析LDA，说到LDA，就不能不提到主成份分析，简称为PCA，是一种非监督学习算法，经常被用来进行数据降维、有损数据压缩、特征抽取、数据可视化（Jolliffe, 2002）。它也被称为Karhunen-Loève变换。

1. PCA原理

PCA的思想是将$n$维特征映射到$k$维空间上$k<n$，这$k$维特征是全新的正交特征，是重新构造出来的$k$维特征，而不是简单地从$n$维特征中去除其余$n-k$维特征。那么如何衡量投影向量的优劣呢？在数学上有三种方法衡量投影的优劣！PCA可以被定义为数据在低维线性空间上的正交投影，这个线性空间被称为主⼦空间（principal subspace），使得投影数据的⽅差被最⼤化（Hotelling, 1933），即最大方差理论。等价地，它也可以被定义为使得平均投影代价最⼩的线性投影，即最小误差理论。平均投影代价是指数据点和它们的投影之间的平均平⽅距离（Pearson, 1901）。还有另一个理论也可以解释PCA原理，即坐标轴相关度理论。这里简单探讨前两种，最后一种在讨论PCA意义时简单概述。

1.1 最大方差理论

在信号处理中认为信号具有较大的方差，噪声有较小的方差，信噪比就是信号与噪声的方差比，越大越好。因此我们认为，最好的$k$维特征是将$n$维样本点变换为$k$维后，每一维上的样本方差都尽可能的大。

首先，考虑在一维空间 (k=1) 上的投影。我们可以使用 $n$ 维向量$u$定义这个空间的方
向。为了方便(并且不失一般性)，我们假定选择一个单位向量，从而 $u^T u = 1$ (注意，我们只对$u$的方向感兴趣，而对 $u$本身的大小不感兴趣)。

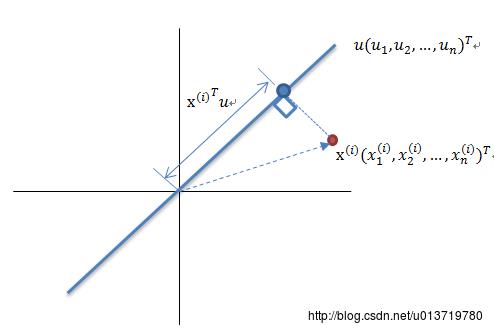
如上图所示，红色点表示原样本点$x^(i)$，$u$是蓝色直线的斜率也是直线的方向向量，而且是单位向量，直线上的蓝色点表示原样本点$x^(i)$在$u$上的投影。容易知道投影点离原点的距离是$x^(i)Tu$，由于这些原始样本点的每一维特征均值都为0，因此投影到u上的样本点的均值仍然是0。

假设原始数据集为$X_mxn$，我们的目标是找到最佳的投影空间$W_nxk=(w_1, w_2, …, w_k)$，其中$w_i$是单位向量且$w_i$与$w_j (i\\neq j)$正交， 何为最佳的$W$？就是原始样本点投影到$W$上之后，使得投影后的样本点方差最大。

由于投影后均值为0，因此投影后的总方差为：

$$\\frac1m\\sum_i=1^m (x^(i)Tw)^2 = \\frac1m\\sum_i=1^m w^T x^(i) x^(i)Tw =\\sum_i=1^m w^T (\\frac1m x^(i) x^(i)T) w_1$$

$\\frac1m x^(i) x^(i)T$是不是似曾相识，没错，它就是原始数据集$X$的协方差矩阵(因为xPCA主成分分析

深入学习主成分分析（PCA）算法原理及其Python实现

主成分分析-PCA

5.7 tensorflow2实现主成分分析(PCA) ——python实战(上篇)

5.7 tensorflow2实现主成分分析(PCA) ——python实战(下篇)

机器学习算法-python实现PCA 主成分分析降维