瓶颈生成树与最小生成树关系的证明
Posted 出尘呢
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了瓶颈生成树与最小生成树关系的证明相关的知识,希望对你有一定的参考价值。
百度百科终于良心易懂了起来qwq
还是算导清楚啊w(゚Д゚)w
https://baike.baidu.com/item/%E7%93%B6%E9%A2%88%E7%94%9F%E6%88%90%E6%A0%91/2397900
定义无向图G,G的瓶颈生成树是一棵 “ 树上最大边权值 edge 在G的所有生成树中最小 ” 的生成树,这样的生成树可能不止一棵。瓶颈生成树的值为树上最大边权值 edge
最小生成树是瓶颈生成树的充分不必要条件。
命题:最小生成树一定是瓶颈生成树。
证明:可以采用反证法予以证明。
假设最小生成树不是瓶颈树,设最小生成树T的最大权边为e,则存在一棵瓶颈树Tb,其所有的边的权值小于w(e)。删除T中的e,形成两棵树T’, T’’,用Tb中连接T’, T’'的边连接这两棵树,得到新的生成树,其权值小于T,与T是最小生成树矛盾。 [1]
命题:瓶颈生成树不一定是最小生成树。
下面是一个反例:
由红色边组成的生成树是一棵瓶颈树,但并非最小生成树。
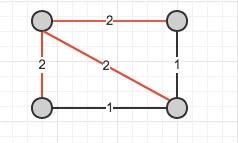
以上是关于瓶颈生成树与最小生成树关系的证明的主要内容,如果未能解决你的问题,请参考以下文章