条件随机场(crf)
Posted pinking
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了条件随机场(crf)相关的知识,希望对你有一定的参考价值。
对于条件随机场的学习,我觉得应该结合HMM模型一起进行对比学习。首先浏览HMM模型:https://www.cnblogs.com/pinking/p/8531405.html
一、定义
条件随机场(crf):是给定一组输入随机变量条件下,另一组输出随机变量的条件概率的分布模型,其特点是假设输出随机变量构成马尔科夫随机场。本文所指线性链条件随机场。
隐马尔科夫模型(HMM):描述由隐藏的马尔科夫链随机生成观测序列的过程,属于生成模型。
当然,作为初学者,从概念上直观感受不到两者的区别与联系,甚至感觉两个概念都理解不了了,不过这没啥问题,继续学下去吧。
二、学习CRF包含的知识点
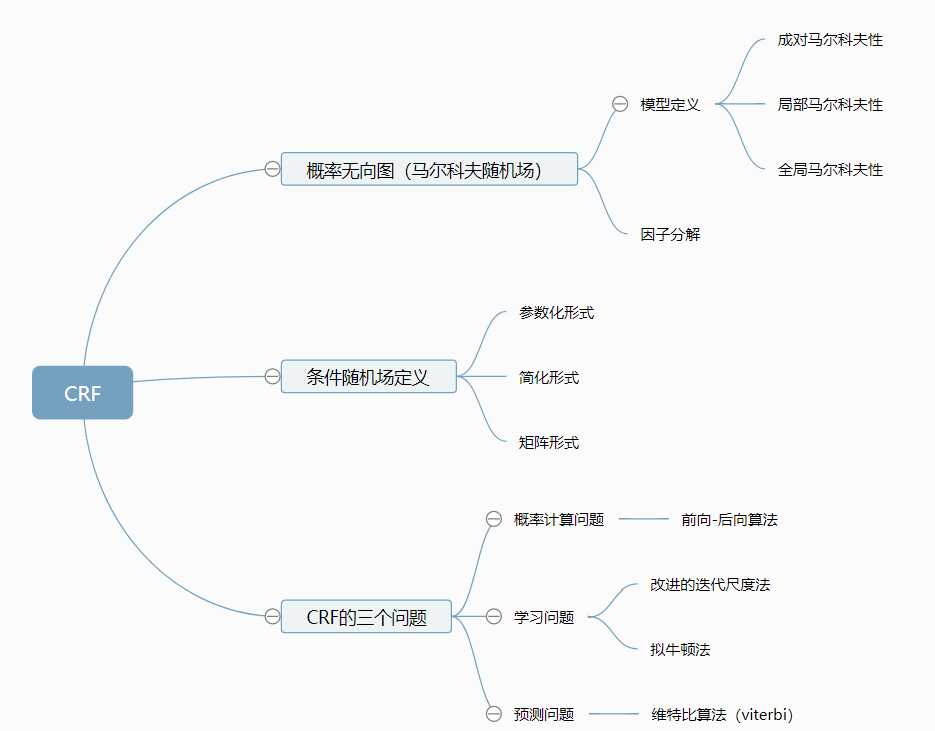
参考李航的统计学习方法,将该部分内容的主要知识点梳理如图,可以看到,CRF和HMM由很多共同点,譬如,都和马尔科夫有关、都有三个问题要解决,解决的方法也有相同的地方。
三、概率无向图
概率无向图,又称马尔科夫随机场,也就是定义中假设输出随机变量构成的。关于模型的构建,其实就是一个由节点(node,记作V)和节点链接关系的边(edge,记作E)组成的图G = (V,E),所谓无向图,就是边没有方向。
随机变量存在的关系包括:成对马尔科夫性、局部马尔科夫性和全局马尔科夫性。假设随机变量的联合概率分布P(Y)和表示它的无向图G,若P(Y)满足上述三种关系,则此联合概率分布为概率无向图或称为马尔科夫随机场。
提出该定义事实上是为了求联合概率分布做铺垫,为了求联合概率,给出无向图中的团与最大团的定义。
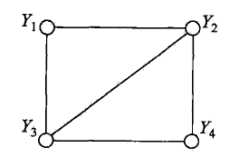
团:{Y1,Y2},{Y1,Y3},{Y2,Y3},{Y2,Y4},{Y3,Y4}
最大团:{Y1,Y2,Y3},{Y4,Y2,Y3}
概率无向图模型的联合概率分布表示为其最大团上的随机变量的函数的乘积的形式的操作。概率无向图模型的链和概率分布P(Y)可以表示为如下形式:
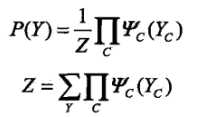
C为无向图的最大团,Yc是C的结点对应的随机变量,Ψ就是一个函数,暂且不用管是什么,就是一个转换关系。
看到这里,其实对于CRF的结果的图的理解已经有了铺垫,实际上,CRF就是将输入X,经过变换,获得输出Y的过程,当然这个Y就满足了上面所画的无向图。但是这个概率是干什么的呢?
继续看CRF的内容,等看完再第四章返回来看该处内容,我相信会有进一步了解,知道概率是怎么求的了吧。
四、条件随机场的定义
突然来的一点感悟,和内容无关:虽然这一章和第一章内容有点重合,但是我觉得作为初学者,最应该的是一个循序渐进的过程,有很多书都是为了内容的连续性,而忽略初学者的接受能力,事实上很多东西需要不断学习,不断深入的过程,这个在很多教程并不能体现出来,而且有时候,网上查问题找资料,总是一搜一大堆,一打开都是一样的,可能是很多人看到别人的博客,学习完了,理解了然后就复制粘贴上了,也懒得再改改或者加点自己的东西。我觉得是可以理解的,最好百度能做一个机制,相同的东西别都索引上了。
条件概率模型:P(Y|X),Y为输出变量,表示标记的序列,X为输入变量,表示需要标注的观测序列(再HMM中也称为状态序列)。
- 学习问题中,利用极大似然估计,估计P^(Y|X)
- 预测问题中,利用给定的序列x,求出条件概率P^(Y|X)最大的输出序列y^
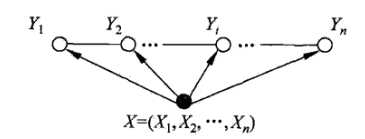
一般的线性链条件随机场表示如图,通常假设X和Y有相同的结构,那么表示图就如下所示:
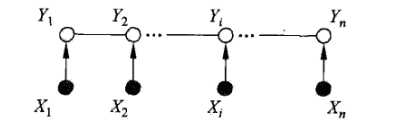
而此时,最大团,就是相邻两个结点的集合。可以引出公式:
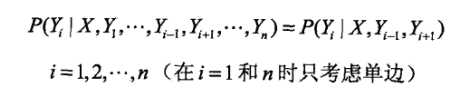
当然,后续会有CRF的参数化形式、简化形式等表示形式,但实际上都是第三章求概率的表达。
五、CRF的三个需要解决的问题
5.1 概率计算问题
条件随机场的概率计算问题,就是给定x,y,求它的P(Yi = yi | x),P(Yi-1 = yi-1 ,Yi = yi | x)以及相应的数学期望的问题。其解决手段用的是HMM那样的前向-后向算法。
以上是关于条件随机场(crf)的主要内容,如果未能解决你的问题,请参考以下文章