卡方检验 （Chi-square test / Chi-square goodness-of-fit test)

Posted 2022-11-27 dqhl1990

卡方检验 （Chi-square test / Chi-square goodness-of-fit test)

---

1. 什么是卡方检验

卡方检验是一种以${\chi }^2$分布为基础的用途广泛的假设检验方法。是一种非参数检验方法。它的无效假设$H_0$为：观察频数与期望频数没有显著性差异。

2. 独立性检验 (Independence)

A test of independence assesses whether unpaired observations on two variables, expressed in a contingency table, are independent of each other

独立性检验评估的是，在一个列联表中，不成对的观测对象中的两个变量是不是相互独立的

以下面的表格为例，我们来探究喝牛奶对感冒发病率有没有影响：

实际值	感冒人数	未感冒人数	合计	感冒率
喝牛奶组	43	96	139	30.94%
不喝牛奶组	28	84	112	25.00%
合计	71	180	251	28.29%

2.1 期望值计算

根据无效假设$H_0$，我们假设喝不喝牛奶和感冒与否并没有显著性关系，则人群的感冒率为：
$$\frac{43+28}{43+28+96+84}=28.29\%$$
则对于上述的实验对象，我们能够得到每个格中的期望值

期望值	感冒人数	未感冒人数	合计	感冒率
喝牛奶组	139 * (1-0.2829)	139*0.2829	139	28.29%
不喝牛奶组	112*(1-0.2829)	112*0.2829	112	28.29%
合计	71	180	251	28.29%

卡方检验就是用来比较实际值与期望值是不是有显著性差异的。如果没有，证明控制变量（喝不喝牛奶）是不会影响因变量（感不感冒）的；有显著性差异，就证明就关系。

2.2 卡方值计算

$${\chi }^2=\sum \frac{(A-E{)}^2}{E}=\sum _{i=1}^k\frac{(A_i-n{p}_i{)}^2}{n{p}_i}\text{\hspace{1em}(1)}$$

其中，$A_i$为单元格$i$中的观察值，$p_i$为单元格$i$中的在$H_0$假设前提下的概率，$k$为单元格数。

上例中${\chi }^2=1.077$

2.3 $H_0$假设拒绝与接受

根据得到的${\chi }^2$值，还并不能直接到的p-value。因为卡方分布根据其自由度有所不同，如下图所示：

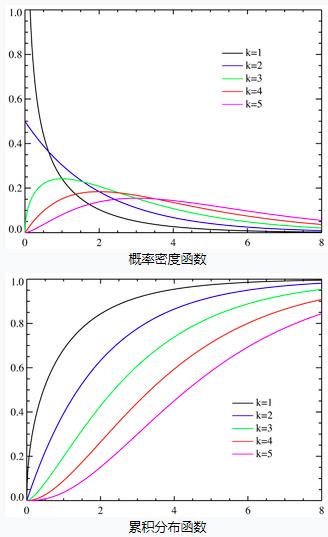
卡方分布的概率密度函数如下：
$$f(x;k)=\begin{array}{ll}\frac{x^{(k/2-1)}{e}^{-x/2}}{2^{k/2}\Gamma (\frac{k}{2})},& x>0\\ 0,& otherwise\end{array}\text{\hspace{1em}(2)}$$
其中$k$为自由度。

所以，首先需要计算所研究样本的自由度
$$k=(R-1)(C-1)\text{\hspace{1em}(3)}$$
其中$R$为单元格的行数，$C$为单元格的列数。
上述例子中，自由度$k=(2-1)(2-1)=1$

根据所给定的自由度$k$以及${\chi }^2$值，即可计算p-value。

对于得到的p-value，与自己指定的显著性水平作比较（通常将0.05作为显著性水平），如果得到的p-value小于0.05，那我们认为样本所表现出来的结果是小概率事件，则我们有理由拒绝原假设$H_0$；否则，我们需要接受原假设$H_0$。

通常情况下，也可以通过查表得形式来选择接受或者拒绝原假设。
如下表：

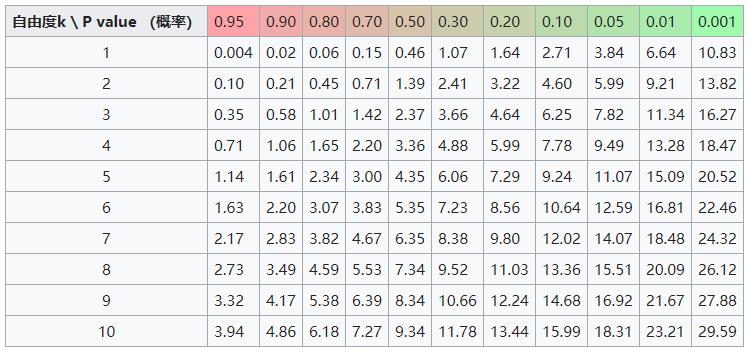
我们看到，${\chi }^2$分布在自由度$k=1$，$p=0.05$时的取值为3.84。我们得到的${\chi }^2$值1.077，小于3.84，且接近于$p=0.3$时的${\chi }^2$值1.07，故不能拒绝原假设$H_0$

---

3 适合度检验 (Goodness of fit)

A test of goodness of fit establishes whether an observed frequency distribution differs from a theoretical distribution

适合度检验展示了一个观察到的频率分布是否与一个理论分布不同。

以掷骰子为例，下表为投掷120次六面骰子的实际观察值：

点数	观察值
1	18
2	19
3	23
4	20
5	16
6	24

3.1 期望值

我们知道，在正常情况下，掷骰子服从二项分布$X\sim B(n,p)$，其数学期望$E[X]=np$，方差为$Var[X]=np(1-p)$。

在进行适合度检验时，我们的原假设$H_0$为观察到的掷骰子结果符合理论上的二项分布（Binomial distribution）。那么，我们就能得到掷骰子的理论值如下表：

点数	观察值
1	20
2	20
3	20
4	20
5	20
6	20

3.2 ${\chi }^2$值计算

根据公式（1），我们得到
$${\chi }^2=2.3$$

3.3 自由度确定

对于适合度检验，自由度的计算按照以下公式：
$$k=C-M$$
其中，$C$为我们观察到的类别数，此例中为6；$M$为我们要比较的理论分布的参数的个数，此例中为1；因此$k=5$。

3.4 $H_0$假设接受与拒绝

通过根据公式（2）或者查表我们能够得到，统计量${\chi }^2=2.3$所对应的p-value大约为0