线性回归法学习笔记

Posted 2022-11-26 周虽旧邦其命维新

1、简单线性回归

所要求得的结果是一个具体的数值，而不是一个类别的话，则该问题是回归问题。只有一个特征的回归问题，成为简单线性回归。两个变量之间存在一次方函数关

系，就称它们之间存在线性关系。拟合就是把平面上一系列的点，用一条光滑的曲线连接起来。

python代码实现思路：

import numpy as np
import matplotlib.pyplot as plt

x_train = np.array([1., 2., 3., 4., 5.])
y_train = np.array([1., 3., 2., 3., 5.])

# plt.scatter(x, y)
# plt.show()

x_mean = np.mean(x_train)
y_mean = np.mean(y_train)

# num 分子，d分母
num = 0.0
d = 0.0

for x_i,y_i in zip(x_train, y_train):
    num += (x_i - x_mean) * (y_i - y_mean)
    d += (x_i - x_mean) ** 2

a = num / d
b = y_mean - a * x_mean
print(a, b)

y_hat = a * x_train + b
plt.scatter(x_train, y_train, color='b')
plt.plot(x_train, y_hat, color='red')
plt.show()

2、向量化和for循环性能比较

编写SimpleLinearRegression.py文件，包含通过for循环和向量化实现的线性回归预测

import numpy as np

# for循环
class SimpleLinearRegression1:
    def __init__(self):
        self.a_ = None
        self.b_ = None

    def fit(self, x_train, y_train):
        x_mean = np.mean(x_train)
        y_mean = np.mean(y_train)

        num = 0.0
        d = 0.0

        for x_i, y_i in zip(x_train, y_train):
            num += (x_i - x_mean) * (y_i - y_mean)
            d += (x_i - x_mean) ** 2

        self.a_ = num / d
        self.b_ = y_mean - self.a_ * x_mean
        return self

    def predict(self, x_predict):
        return np.array([self._predict(x) for x in x_predict])

    def _predict(self, x_predict):
        return self.a_ * x_predict + self.b_


# 向量化
class SimpleLinearRegression2:
    def __init__(self):
        self.a_ = None
        self.b_ = None

    def fit(self, x_train, y_train):
        x_mean = np.mean(x_train)
        y_mean = np.mean(y_train)

        num = 0.0
        d = 0.0

        num = (x_train - x_mean).dot(y_train - y_mean)
        d = (x_train - x_mean).dot(x_train - x_mean)
        # for x_i, y_i in zip(x_train, y_train):
        #     num += (x_i - x_mean) * (y_i - y_mean)
        #     d += (x_i - x_mean) ** 2

        self.a_ = num / d
        self.b_ = y_mean - self.a_ * x_mean
        return self

    def predict(self, x_predict):
        return np.array([self._predict(x) for x in x_predict])

    def _predict(self, x_predict):
        return self.a_ * x_predict + self.b_

测试

import numpy as np
from SimpleLinearRegression import SimpleLinearRegression1
from SimpleLinearRegression import SimpleLinearRegression2
import time

x_train = np.array([1., 2., 3., 4., 5.])
y_train = np.array([1., 3., 2., 3., 5.])
lineRegression = SimpleLinearRegression1()
lineRegression.fit(x_train, y_train)
print(lineRegression.predict([6.]))

# for循环与向量化的性能测试对比

m = 1000000

big_x = np.random.random(size=m)
big_y = big_x * 2.0 + 1.5 + np.random.normal(size=m)
for_start = time.time()
lineRegression = SimpleLinearRegression1()
lineRegression.fit(big_x, big_y)
for_end = time.time()
print(for_end - for_start)

vector_start = time.time()
lineRegression2 = SimpleLinearRegression2()
lineRegression2.fit(big_x, big_y)
vector_end = time.time()
print(vector_end - vector_start)

print(lineRegression.a_, lineRegression.b_)
print(lineRegression2.a_, lineRegression2.b_)

3、指标MSE,RMS,MAE,R Squared

编写metrics.py文件

import numpy as np
from math import sqrt

def accuracy_score(y_true, y_predict):
    return sum(y_true == y_predict)/len(y_true)

# 计算预测结果的均方误差
def mean_squared_error(y_ture, y_predict):
    return np.sum((y_predict - y_ture) ** 2) / len(y_ture)

# 计算预测结果的均方根误差
def root_mean_squared_error(y_ture, y_predict):
    return sqrt(mean_squared_error(y_ture, y_predict))

# 计算预测结果的平均误差
def mean_absolute_error(y_ture, y_predict):
    return np.sum(np.absolute(y_predict - y_ture)) / len(y_ture)
    
# 计算预测结果的R Squared
def r_squared_score(y_ture, y_predict):
    return 1 - mean_squared_error(y_ture, y_predict) / np.var(y_ture)

在SimpleLinearRegression2中添加线性回归评分方法：

from common.metrics import r_squared_score

    def score(self, x_predict, y_true):
        y_predict = np.array([self._predict(x) for x in x_predict])
        return r_squared_score(y_true, y_predict)

使用波士顿房产数据训练模型和测试模型预测结果

import numpy as np
from sklearn import datasets
from common.model_selection import TrainTestSplit
from SimpleLinearRegression import SimpleLinearRegression2
from math import sqrt
from common.metrics import mean_absolute_error
from common.metrics import root_mean_squared_error
from common.metrics import mean_squared_error
from sklearn.metrics import mean_squared_error as sk_mean_squared_error
from sklearn.metrics import mean_absolute_error as sk_mean_absolute_error

boston = datasets.load_boston()
# DESCR查看数据集文档
# print(boston.DESCR)
print(type(boston),boston.feature_names)
x = boston.data[:,5]
y = boston.target
print(x.shape, y.shape)

# 真实数据可能会有上限值，这些在上限值的数据可能不是真实数据，所以只保留小于最大值的数据用来训练
y_max = np.max(y)
print(y_max)
x = x[y < y_max]
y = y[y < y_max]
print(x.shape, y.shape)

x_train,x_test,y_train,y_test = TrainTestSplit.train_test_split(x=x, y=y, seed=666)
simpleLinear = SimpleLinearRegression2()
simpleLinear.fit(x_train=x_train, y_train=y_train)
y_predict = simpleLinear.predict(x_test)
print(y_predict)
print(y_test)

# plt.scatter(x, y)
# plt.show()

# 计算测试集预测结果的均方误差
mse_test = np.sum((y_predict - y_test) ** 2) / len(y_test)
print(mse_test)

# 计算测试集预测结果的均方根误差
rmse_test = sqrt(mse_test)
print(rmse_test)

# 计算测试集预测结果的平均误差
mae_test = np.sum(np.absolute(y_predict - y_test)) / len(y_test)
print(mae_test)

# 使用抽取出的自定义文件metrics.py中的计算误差方法
print(mean_squared_error(y_test, y_predict))
print(root_mean_squared_error(y_test, y_predict))
print(mean_absolute_error(y_test, y_predict))

# 使用sklearn.metrics封装的计算误差方法，sklearn中没有提供rmse方法，需要通过mse的结果自己开平方
print(sk_mean_squared_error(y_test, y_predict))
print(sqrt(sk_mean_squared_error(y_test, y_predict)))
print(sk_mean_absolute_error(y_test, y_predict))

print('=============================================')
# R Squared：1-(mse/var(y))
print(1-sk_mean_squared_error(y_test, y_predict)/np.var(y_test))
# 使用自定义metrics中计算r2的方法
print(r_squared_score(y_test, y_predict))
print(simpleLinear.score(x_test, y_test))

最好的衡量线性回归法的指标 R Squared：

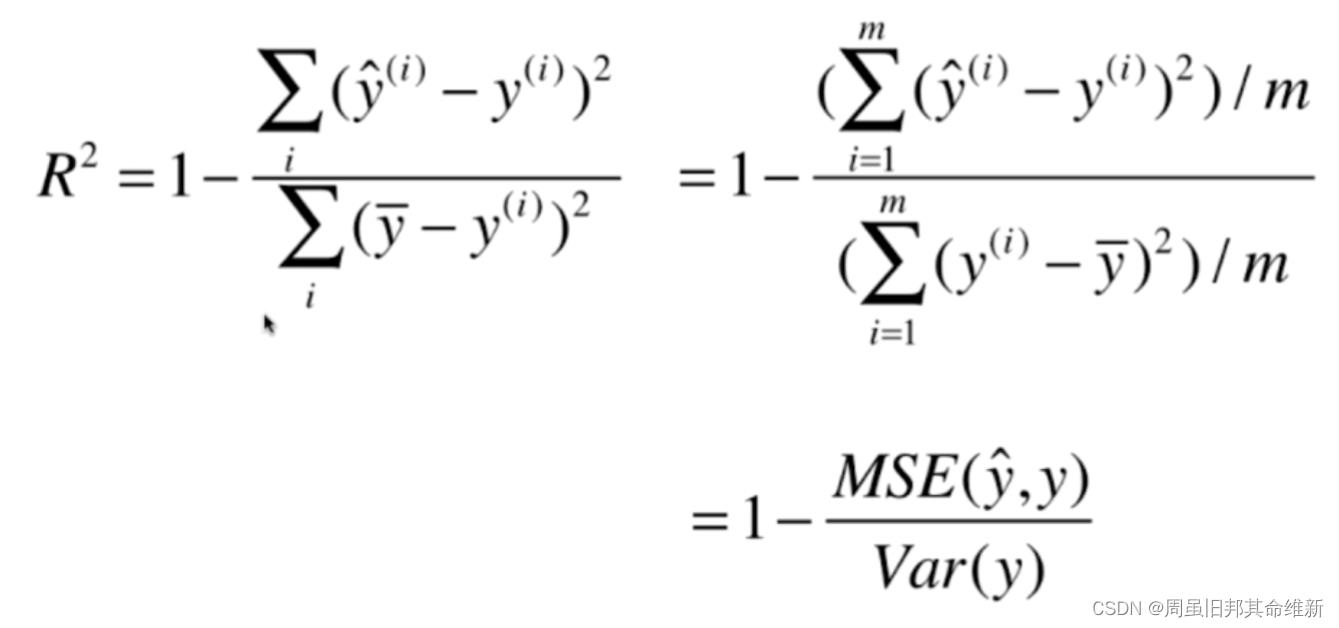
4、多元线性回归

4.1 理论推导

推导过程：

这里用到了矩阵相乘的知识，矩阵相乘，结果等于前一个矩阵的行乘以后一个矩阵的列再求和

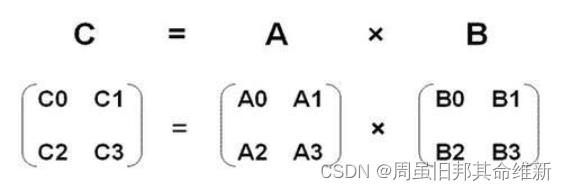
设Y=y的真实值-y的预测值，根据矩阵相乘的知识，上面的目标1即等于：Y的转置*Y，将Y的值代入即目标2。

推导过程比较复杂，可直接使用如下推导结果（感兴趣的可以从书中或者互联网查阅推导结果）：

就称为多元线性回归的正规方程解（Normal Equation)

其实，所求解是存在问题的，我们使用朴素的矩阵的运算方式求解此式的时间复杂度是比较高的，为 O(n^3)，虽然对于解决

矩阵是有一些加速方案的，但使用加速方案，整体优化出来也是O(n^2.4)。

这样做也有一个优点，就是不需要对数据做归一化处理。

4.2 手写实现多元线性回归思想

import numpy as np
from common.metrics import r_squared_score

class LinearRegression:
    def __init__(self):
        # 系数coefficient θ1到θn，是一个向量
        self.coef_ = None
        # 截距 θ0，是一个数值
        self.interception_ = None
        self._theta = None

    def fit_normal(self, X_train, y_train):
        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        # np.linalg.inv逆矩阵
        self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
        self.interception_ = self._theta[0]
        self.coef_ = self._theta[1:]
        return self

    # y预测结果 = Xb * theta
    def predict(self, X_predict):
        X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
        return X_b.dot(self._theta)

    def score(self, X_test, y_test):
        y_predict = self.predict(X_test)
        return r_squared_score(y_test, y_predict)

测试：

import numpy as np
from sklearn import datasets
from LinearRegression import LinearRegression
from common.model_selection import TrainTestSplit

boston = datasets.load_boston()
X = boston.data
y = boston.target
X = X[y < 50.0]
y = y[y < 50.0]

X_train,X_test,y_train,y_test = TrainTestSplit.train_test_split(x=X, y=y, seed=666)

linearRegression = LinearRegression()
linearRegression.fit_normal(X_train=X_train, y_train=y_train)
# print(linearRegression.predict(X_test))
# print(X_test)
print(linearRegression.score(X_test, y_test))

4.3 scikit-learn多元线性回归预测波斯顿房价

import numpy as np
from sklearn import datasets
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split

boston = datasets.load_boston()
X = boston.data
y = boston.target
X = X[y < 50.0]
y = y[y < 50.0]

X_train,X_test,y_train,y_test = train_test_split(X, y)
reg = LinearRegression()
reg.fit(X=X_train, y=y_train)
print(reg.score(X=X_test, y = y_test))

print(reg.coef_)
print(reg.intercept_)


# 系数的正负表示特征与预测结果是正相关还是负相关，系数的绝对值决定了影响的程度
print('==========================================')
print(reg.coef_)
print(reg.intercept_)
# 查看哪些特征对预测结果的影响比较大
print(boston.feature_names[np.argsort(reg.coef_)])

4.4 scikit-learn knn算法预测波斯顿房价

import numpy as np
from sklearn import datasets
from sklearn.neighbors import KNeighborsRegressor
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
import time

boston = datasets.load_boston()
X = boston.data
y = boston.target
X = X[y < 50.0]
y = y[y < 50.0]

X_train,X_test,y_train,y_test = train_test_split(X, y)

# KNeighborsRegressor回归问题，KNeighborsClassifier分类问题
knn_reg = KNeighborsRegressor()

param_grid = [
    
        'weights':['uniform'],
        'n_neighbors':[i for i in range(1,11)]
    ,
    
        'weights':['distance'],
        'n_neighbors':[i for i in range(1,11)],
        'p':[i for i in range(1,6)]
    
]
grid_search = GridSearchCV(knn_reg, param_grid, n_jobs=-1, verbose=1)

time_start = time.time()
grid_search.fit(X=X_train,y=y_train)
time_end = time.time()
# 计算的时间差为程序的执行时间，单位为秒
print(time_end-time_start)
print(grid_search.best_params_)
print(grid_search.best_score_)
# 网格搜索超参数结果'n_neighbors': 8, 'p': 1, 'weights': 'distance'
print(grid_search.best_estimator_.score(X_test, y_test))