梯度下降法学习笔记
Posted 周虽旧邦其命维新
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了梯度下降法学习笔记相关的知识,希望对你有一定的参考价值。
1、梯度下降法思路
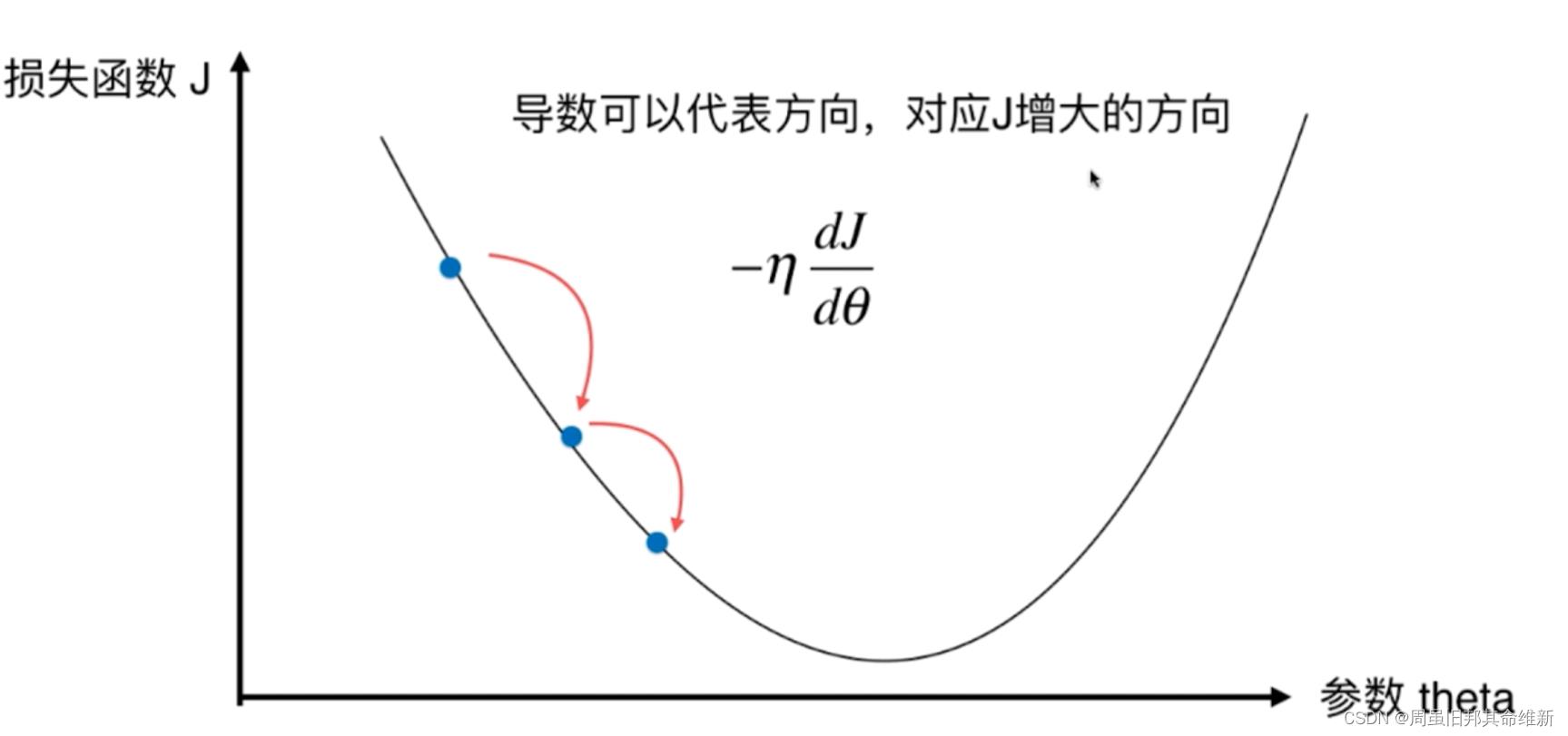
注释中原函数指损失函数,以下均是如此
import numpy as np
import matplotlib.pyplot as plt
plot_x = np.linspace(-1, 6, 141)
plot_y = (plot_x - 2.5) ** 2 - 1
# 导函数
def dJ(theta):
return 2 * (theta -2.5)
# 原函数
def J(theta):
return (theta - 2.5) ** 2 - 1
# 步长,自变量每次循环移动的量
eta = 0.1
# theta自变量,0.0梯度下降初始点
theta = 0.0
epsilon = 1e-8
while True:
# 当前点的导数值
gradient = dJ(theta)
last_theta = theta
# 自变量的变化量 * 当前点的导数值 = 损失函数的变化量
# 导数的正负值代表损失函数在当前点的变化趋势是增大还是减小,因此如果导数为负则theta增加,损失函数趋于变小
# 如果导数为正,则theta减小,损失函数趋于变小,因此theta减去导数值,损失函数趋于变小
# 在eta合适的情况下,随着循环进行,导数值逐渐趋近0,eta是常数,损失函数的变化量会越来越小
theta = theta - eta * gradient
# abs求绝对值
if abs(J(theta) - J(last_theta)) < epsilon:
break
print(theta)
print(J(theta))
theta = 0.0
theta_history = [theta]
while True:
# 当前点的导数值
gradient = dJ(theta)
last_theta = theta
# 自变量的变化量 * 当前点的导数值 = 损失函数的变化量
# 导数的正负值代表损失函数在当前点的变化趋势是增大还是减小,因此如果导数为负则theta增加,损失函数趋于变小
# 如果导数为正,则theta减小,损失函数趋于变小,因此theta减去导数值,损失函数趋于变小
# 在eta合适的情况下,随着循环进行,导数值逐渐趋近0,eta是常数,损失函数的变化量会越来越小
theta = theta - eta * gradient
theta_history.append(theta)
# abs求绝对值
if abs(J(theta) - J(last_theta)) < epsilon:
break
plt.plot(plot_x, J(plot_x), color='y')
plt.plot(np.array(theta_history), J(np.array(theta_history)), color='r', marker='+')
plt.show()
print(len(theta_history))
2、线性回归中的梯度下降法
2.1 多元线性回归梯度下降公式


2.2 代码实现梯度下降法
编写gradient_descent.py文件,使用梯度下降法计算多元线性回归问题中使损失函数最小的系数和截距:
import numpy as np
def gradient_descent(X_b, y, theta_init, eta, n_iters=1e4, epsilon=1e-8):
theta = theta_init
i_iter = 1
while i_iter < n_iters:
# 当前点的导数值
gradient = dJ(theta, X_b, y)
last_theta = theta
# 自变量的变化量 * 当前点的导数值 = 损失函数的变化量
# 导数的正负值代表损失函数在当前点的变化趋势是增大还是减小,因此如果导数为负则theta增加,损失函数趋于变小
# 如果导数为正,则theta减小,损失函数趋于变小,因此theta减去导数值,损失函数趋于变小
# 在eta合适的情况下,随着循环进行,导数值逐渐趋近0,eta是常数,损失函数的变化量会越来越小
theta = theta - eta * gradient
# abs求绝对值
if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
break
i_iter += 1
return theta
# 原函数
def J(theta, X_b, y):
return np.sum(((y - X_b.dot(theta)) ** 2)) / len(X_b)
# 导函数
def dJ(theta, X_b, y):
res = np.empty(len(theta))
res[0] = np.sum(X_b.dot(theta) - y)
for i in range(1, len(theta)):
res[i] = np.sum((X_b.dot(theta) - y).dot(X_b[:,i]))
return res * 2 / (len(X_b))
使用测试数据通过梯度下降法获得系数和截距:
import numpy as np
import matplotlib.pyplot as plt
from gradient_descent import gradient_descent
x = 4 * np.random.rand(100)
y = 2. * x + 5. + np.random.normal(size=100)
X = x.reshape(-1, 1)
# plt.scatter(x=X, y=y)
# plt.show()
X_b = np.hstack([np.ones((len(X), 1)), X])
theta_init = np.zeros(X_b.shape[1])
eta = 0.01
print(gradient_descent(X_b=X_b, y = y, theta_init=theta_init, eta=eta))
2.3 结合多元线性回归代码
重新封装线性回归章节的LinearRegression.py
import numpy as np
from common.metrics import r_squared_score
class LinearRegression:
def __init__(self):
# 系数coefficient θ1到θn,是一个向量
self.coef_ = None
# 截距 θ0,是一个数值
self.interception_ = None
self._theta = None
def fit_normal(self, X_train, y_train):
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
# np.linalg.inv逆矩阵
self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
self.interception_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4, epsilon=1e-8):
# 原函数
def J(theta, X_b, y):
return np.sum(((y - X_b.dot(theta)) ** 2)) / len(X_b)
# 导函数
def dJ(theta, X_b, y):
res = np.empty(len(theta))
res[0] = np.sum(X_b.dot(theta) - y)
for i in range(1, len(theta)):
res[i] = np.sum((X_b.dot(theta) - y).dot(X_b[:, i]))
return res * 2 / (len(X_b))
def gradient_descent(X_b, y, theta_init, eta, n_iters=1e4, epsilon=1e-8):
theta = theta_init
i_iter = 1
while i_iter < n_iters:
# 当前点的导数值
gradient = dJ(theta, X_b, y)
last_theta = theta
# 自变量的变化量 * 当前点的导数值 = 损失函数的变化量
# 导数的正负值代表损失函数在当前点的变化趋势是增大还是减小,因此如果导数为负则theta增加,损失函数趋于变小
# 如果导数为正,则theta减小,损失函数趋于变小,因此theta减去导数值,损失函数趋于变小
# 在eta合适的情况下,随着循环进行,导数值逐渐趋近0,eta是常数,损失函数的变化量会越来越小
theta = theta - eta * gradient
# abs求绝对值
if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
break
i_iter += 1
return theta
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
theta_init = np.zeros(X_b.shape[1])
self._theta = gradient_descent(X_b=X_b, y=y_train, theta_init=theta_init, eta=eta, n_iters=n_iters, epsilon=epsilon)
self.interception_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
# y预测结果 = Xb * theta
def predict(self, X_predict):
X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
return X_b.dot(self._theta)
def score(self, X_test, y_test):
y_predict = self.predict(X_test)
return r_squared_score(y_test, y_predict)
测试:
import numpy as np
from common.LinearRegression import LinearRegression
x = 4 * np.random.rand(100)
y = 2. * x + 5. + np.random.normal(size=100)
X = x.reshape(-1, 1)
lin_reg = LinearRegression()
lin_reg.fit_gd(X_train=X, y_train=y)
print(lin_reg.interception_)
print(lin_reg.coef_)
3、向量化和归一化
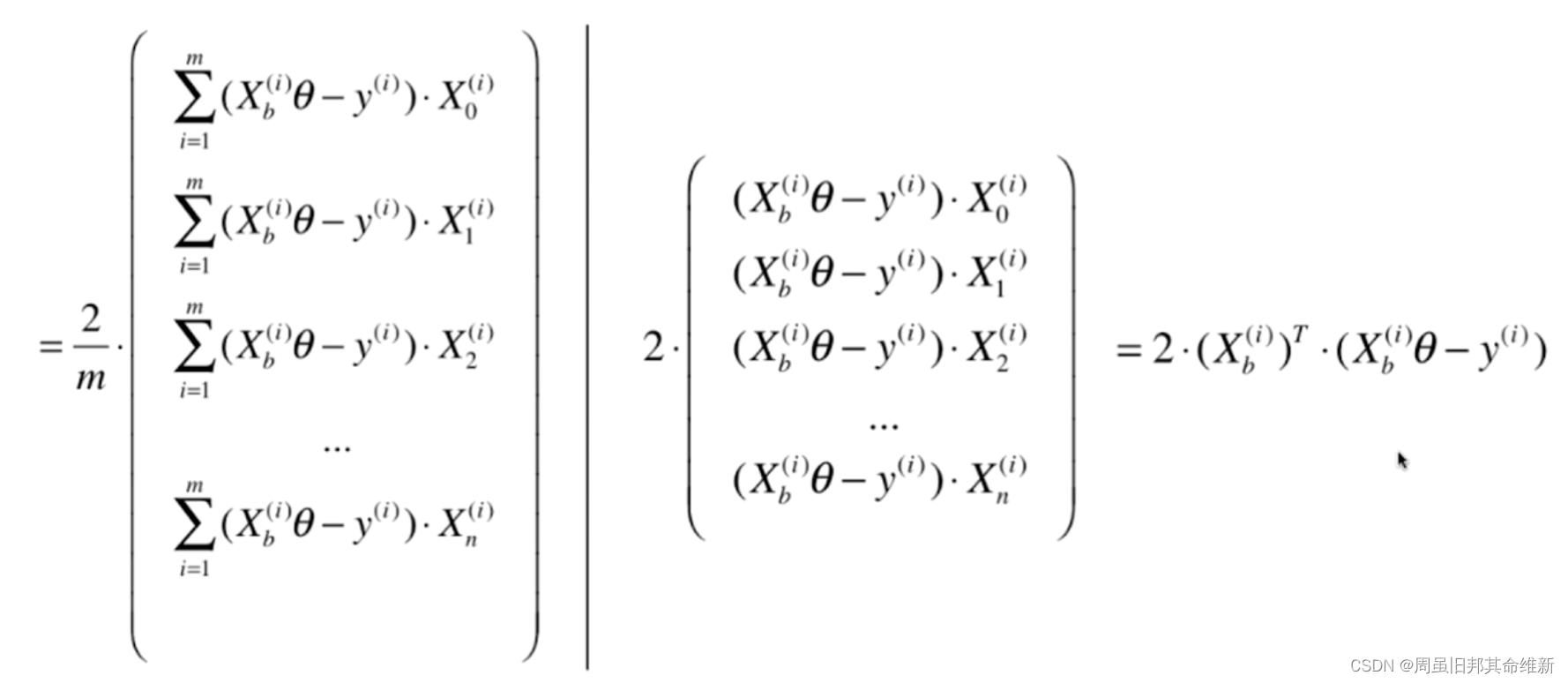
3.1 公式推导

最终损失函数的导函数就变成了:
2/m * Xb的转置 * (Xb * theta-y)
3.2 向量化和归一化代码实现
修改LinearRegression.py中的导函数:
# 导函数
def dJ(theta, X_b, y):
# 2/m * Xb的转置 * (Xb * theta-y)
return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(X_b)
测试:
from sklearn import datasets
from common.LinearRegression import LinearRegression
from common.model_selection import TrainTestSplit
from sklearn.preprocessing import StandardScaler
boston = datasets.load_boston()
X = boston.data
y = boston.target
X = X[y < 50.0]
y = y[y < 50.0]
X_train,X_test,y_train,y_test = TrainTestSplit.train_test_split(x=X, y=y, seed=666)
lin_reg = LinearRegression()
lin_reg.fit_normal(X_train=X_train,y_train=y_train)
print(lin_reg.score(X_test=X_test,y_test=y_test))
lin_reg.fit_gd(X_train=X_train, y_train=y_train, eta=0.000001, n_iters=1e6)
print(lin_reg.coef_)
print(lin_reg.interception_)
print('=====================================')
print(lin_reg.score(X_test=X_test, y_test=y_test))
# 由于不同特征数据规模相差非常大,有的可能是零点几,有的是几百,这时eta如果非常小,则训练过程非常耗时,
# 如果eta不够小,又会出现stackflow,所以在模型训练之前我们先要对数据进行归一会处理
stander = StandardScaler()
stander.fit(X_train)
X_train_stand = stander.transform(X_train)
X_test_stand = stander.transform(X_test)
lin_reg2 = LinearRegression()
lin_reg2.fit_gd(X_train_stand, y_train)
print(lin_reg2.score(X_test_stand, y_test))
3.3 梯度下降法的优势
import numpy as np
from common.LinearRegression import LinearRegression
import time
m = 1000
n = 5000
big_X = np.random.normal(size=(m, n))
true_theta = np.random.uniform(0.0, 100.0, size=n+1)
big_y = big_X.dot(true_theta[1:]) + true_theta[0] + np.random.normal(0., 10., size=m)
lin_reg = LinearRegression()
start_time = time.time()
lin_reg.fit_normal(X_train=big_X, y_train=big_y)
end_time = time.time()
print(end_time - start_time)
start_time = time.time()
lin_reg.fit_gd(X_train=big_X, y_train=big_y)
end_time = time.time()
print(end_time - start_time)
# 在我的机器上,当特征值有5000个时,梯度下降比常规方程解稍快,
# 当特征值增加一倍,梯度下降法的训练时间几乎不变,而常规方程解的方式训练时间大约*7
4、随机梯度下降法(SGD)
4.1 公式推导
SGD算法是从样本中随机抽出一组,训练后按梯度更新一次,然后再抽取一组,再更新一次,在样本量及其大的情况下,可能不用训练完所有的样本就可以获得一
个损失值在可接受范围之内的模型了。(重点:每次迭代使用一组样本。)
为什么叫随机梯度下降算法呢?这里的随机是指每次迭代过程中,样本都要被随机打乱,这个也很容易理解,打乱是有效减小样本之间造成的参数更新抵消问题。
模拟退火指的是逐渐缩小学习率在训练的过程中,因为在训练的后期,需要使用比较小的学习率进行训练,这是因为前期的训练过程中,模型的参数基本已经确
定,我们不希望他过大的变化,所以慢慢的训练以至于达到不错的拟合。
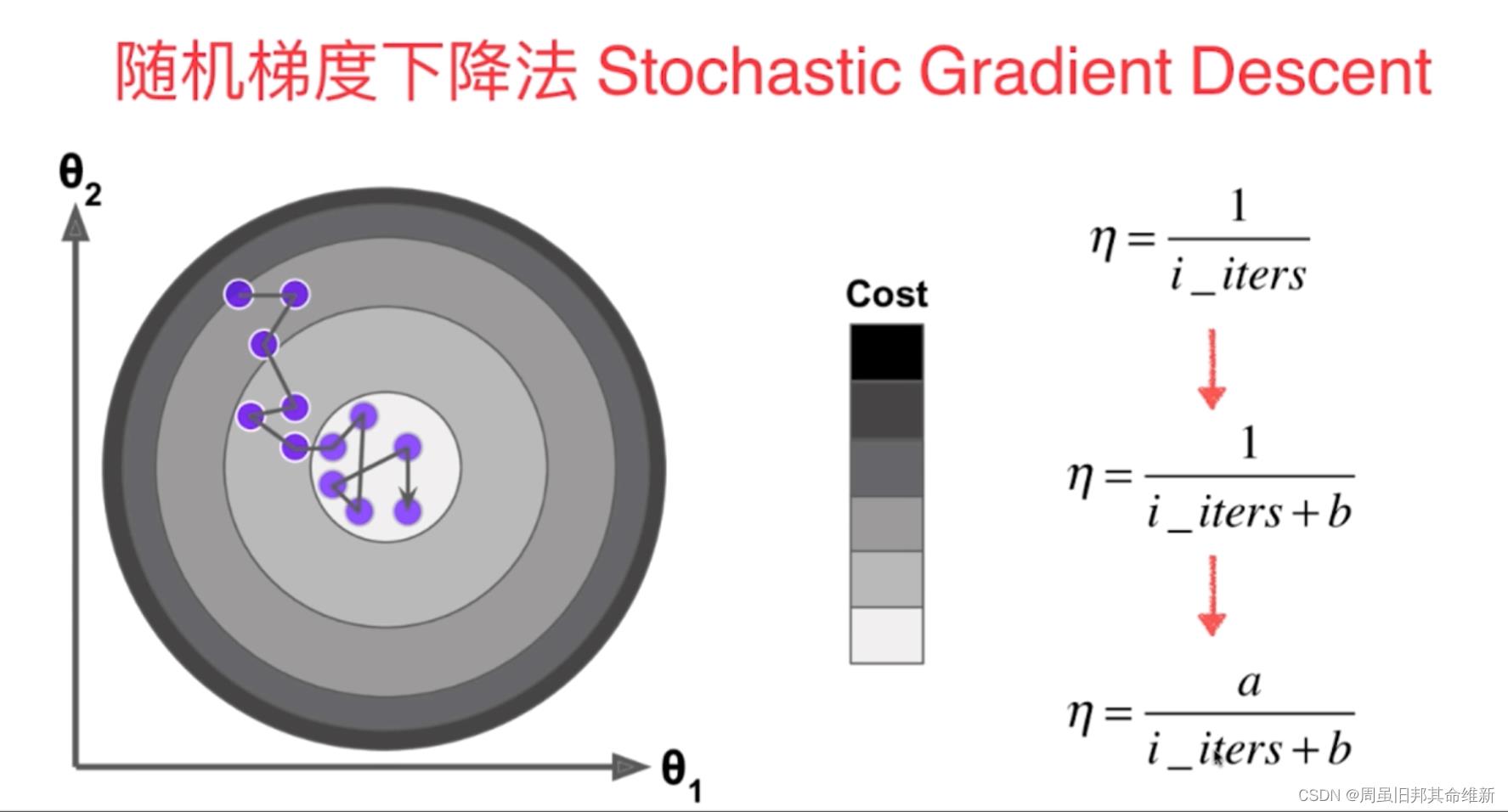
因为学习率是随时间逐渐缩小,所以式子中的a和b有时候也写作t0和t1。
4.2 代码实现
编写gradient_descent.py文件
import numpy as np
# 批量梯度下降
def gradient_descent(X_b, y, theta_init, eta, n_iters=1e4, epsilon=1e-8):
theta = theta_init
i_iter = 1
while i_iter < n_iters:
# 当前点的导数值
gradient = dJ(theta, X_b, y)
last_theta = theta
# 自变量的变化量 * 当前点的导数值 = 损失函数的变化量
# 导数的正负值代表损失函数在当前点的变化趋势是增大还是减小,因此如果导数为负则theta增加,损失函数趋于变小
# 如果导数为正,则theta减小,损失函数趋于变小,因此theta减去导数值,损失函数趋于变小
# 在eta合适的情况下,随着循环进行,导数值逐渐趋近0,eta是常数,损失函数的变化量会越来越小
theta = theta - eta * gradient
# abs求绝对值
if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
break
i_iter += 1
return theta
# 随机梯度下降
def sgd(X_b, y, theta_init, n_iters=1e4):
t0 = 5
t1 = 50
# 返回学习率(eta),随循环次数减少
def learn_rate(t):
return t0/(t + t1)
theta = theta_init
for cur_iter in range(n_iters):
# 每次迭代抽取一个样本计算导数值
rand_i = np.random.randint(0, len(X_b))
gradient = dJ_sgd(theta=theta, X_b_i=X_b[rand_i], y_i=y[rand_i])
# 即1.1代码中的theta变化方式theta = theta - eta * gradient
theta = theta - learn_rate(cur_iter) * gradient
return theta
# 原函数
def J(theta, X_b, y):
return np.sum(((y - X_b.dot(theta)) ** 2)) / len(X_b)
# 导函数
def dJ(theta, X_b, y):
return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(X_b)
# 返回某一个样本的导数值
def dJ_sgd(theta, X_b_i, y_i):
return X_b_i.T.dot(X_b_i.dot(theta) - y_i) * 2.
测试代码:
import numpy as np
import matplotlib.pyplot as plt
from gradient_descent import gradient_descent
from gradient_descent import sgd
import time
m = 100000
x = np.random.normal(size=m)
X = x.reshape(-1,1)
y = 2. * x + 5. + np.random.normal(0, 3, size=m)
# 批量梯度下降法
X_b = np.hstack([np.ones(shape=(len((X)), 1)), X])
theta_init = np.zeros(X_b.shape[1])
eta = 0.01
start_time = time.time()
print(gradient_descent(X_b=X_b,y=y, theta_init=theta_init, eta=eta))
end_time = time.time()
print(end_time - start_time)
# 随机梯度下降法
X_b = np.hstack([np.ones(shape=(len((X)), 1)), X])
theta_init = np.zeros(X_b.shape[1])
eta = 0.01
start_time = time.time()
print(sgd(X_b=X_b, y=y, theta_init=theta_init, n_iters=len(X_b)//3))
end_time = time.time()
print(end_time - start_time)
测试结果如下,精度略有损失,速度快了很多。
[5.01251289 2.00847791]
1.0882823467254639
[5.01067864 2.01782428]
0.3111999034881592
4.3 封装LinearRegression.py
import numpy as np
from common.metrics import r_squared_score
class LinearRegression:
def __init__(self):
# 系数coefficient θ1到θn,是一个向量
self.coef_ = None
# 截距 θ0,是一个数值
self.interception_ = None
self._theta = None
def fit_normal(self, X_train, y_train):
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
# np.linalg.inv逆矩阵
self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
self.interception_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4, epsilon=1e-8):
# 原函数
def J(theta, X_b, y):
return np.sum(((y - X_b.dot(theta)) ** 2)) / len(X_b)
# 导函数
def dJ(theta, X_b, y):
# res = np.empty(len(theta))
# res[0] = np.sum(X_b.dot(theta) - y)
# for i in range(1, len(theta)):
# res[i] = np.sum((X_b.dot(theta) - y).dot(X_b[:, i]))
# return res * 2 / (len(X_b))
# 2/m * Xb的转置 * (Xb * theta-y)
return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(X_b)
def gradient_descent(X_b, y, theta_init, eta, n_iters=1e4, epsilon=1e-8):
theta = theta_init
i_iter = 1
while i_iter < n_iters:
# 当前点的导数值
gradient = dJ(theta, X_b, y)
last_theta = theta
# 自变量的变化量 * 当前点的导数值 = 损失函数的变化量
# 导数的正负值代表损失函数在当前点的变化趋势是增大还是减小,因此如果导数为负则theta增加,损失函数趋于变小
# 如果导数为正,则theta减小,损失函数趋于变小,因此theta减去导数值,损失函数趋于变小
# 在eta合适的情况下,随着循环进行,导数值逐渐趋近0,eta是常数,损失函数的变化量会越来越小
theta = theta - eta * gradient
# abs求绝对值
if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
break
i_iter += 1
return theta
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
theta_init = np.zeros(X_b.shape[1])
self._theta = gradient_descent(X_b=X_b, y=y_train, theta_init=theta_init, eta=eta, n_iters=n_iters, epsilon=epsilon)
self.interception_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
def fit_sgd(self, X_train, y_train, n_iters=5):
# 返回某一个样本的导数值
def dJ_sgd(theta, X_b_i, y_i):
return X_b_i.T.dot(X_b_i.dot(theta) - y_i) * 2.
# 随机梯度下降
def sgd(X_b, y, theta_init, n_iters=1e4):
t0 = 5
t1 = 50
# 返回学习率(eta),随循环次数减少
def learn_rate(t):
return t0 / (t + t1)
theta = theta_init
m = len(X_b)
# 将所有数据循环n_iters遍
for cur_iter in range(n_iters):
indexes = np.random.permutation(m)
X_b_new = X_b[indexes]
y_new = y[indexes]
for i in range(m):
# 每次迭代抽取一个样本计算导数值
gradient = dJ_sgd(theta=theta, X_b_i=X_b_new[i], y_i=y_new[i])
# 即1.1代码中的theta变化方式theta = theta - eta * gradient
theta = theta - learn_rate(cur_iter * m + i) * gradient
return theta
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
theta_init = np.zeros(X_b.shape[1])
self._theta = sgd(X_b=X_b, y=y_train, theta_init=theta_init, n_iters=n_iters)
self.interception_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
# y预测结果 = Xb * theta
def predict(self, X_predict):
X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
return X_b.dot(self._theta)
def score(self, X_test, y_test):
y_predict = self.predict(X_test)
return r_squared_score(y_test, y_predict)
测试LinearRegression中的随机梯度下降算法:
import numpy as np
import matplotlib.pyplot as plt
import time
from common.LinearRegression import LinearRegression
m = 100000
x = np.random.normal(size=m)
X = x.reshape(-1,1)
y = 2. * x + 5. + np.random.normal(0, 3, size=m)
lin_reg = LinearRegression()
lin_reg.fit_sgd(X_train=X, y_train=y, n_iters=2)
print(lin_reg.coef_)
print(lin_reg.interception_)
使用LinearRegression中的随机梯度下降算法训练波士顿房价模型:
from sklearn import datasets
from common.LinearRegression import LinearRegression
from common.model_selection import TrainTestSplit
from sklearn.preprocessing import StandardScaler
boston = datasets.load_boston()
X = boston.data
y = boston.target
X = X[y < 50.0]
y = y[y < 50.0]
X_train,X_test,y_train,y_test = TrainTestSplit.train_test_split(x=X, y=y, seed=666)
stander = StandardScaler()
stander.fit(X_train)
X_train = stander.transform(X_train)
X_test = stander.transform(X_test)
lin_reg = LinearRegression()
lin_reg.fit_sgd(X_train=X_train, y_train=y_train, n_iters=2)
print(lin_reg.score(X_test=X_test, y_test=y_test))
4.4 scikilearn中的梯度下降法
from sklearn import datasets
from sklearn.linear_model import SGDRegressor
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
boston = datasets.load_boston()
X = boston.data
y = boston.target
X = X[y < 50.0]
y = y[y < 50.0]
X_train,X_test,y_train,y_test = train_test_split(X,y)
stander = StandardScaler()
stander.fit(X_train)
X_train = stander.transform(X_train)
X_test = stander.transform(X_test)
# max_iter用来指定神经网络的最大迭代次数,默认值为1000
# n_iter_no_change,每当超过n_iter_no_change参数的迭代次数损失函数没有显著变化时,训练停止。默认值为5
sgd_reg = SGDRegressor(max_iter=100000, n_iter_no_change=100)
sgd_reg.fit(X=X_train,y=y_train)
print(sgd_reg.score(X=X_test, y=y_test))
5、梯度的调试
5.1 公式推导
一维空间曲线上某一点的导数计算
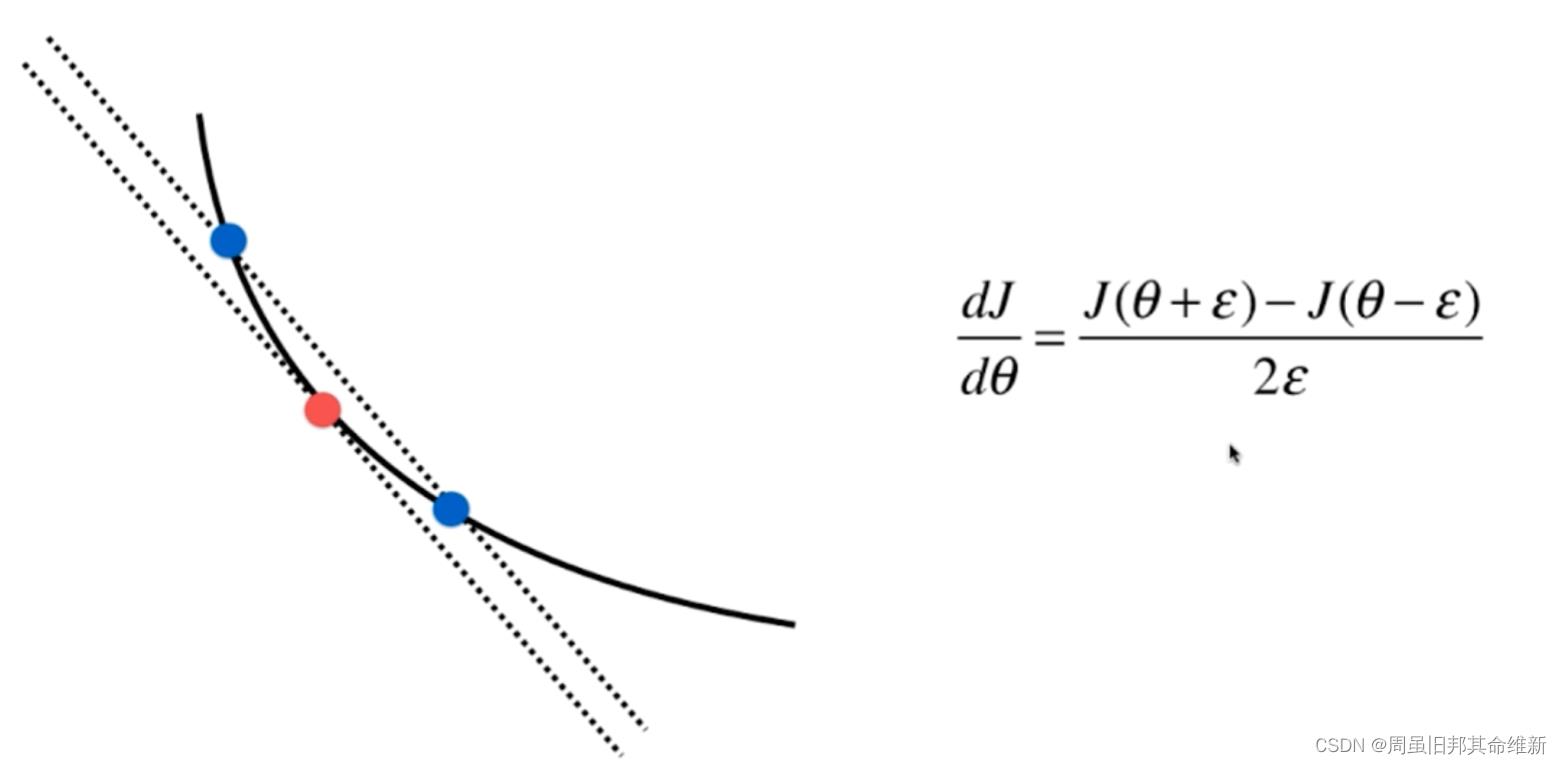
多维空间某一点的梯度计算
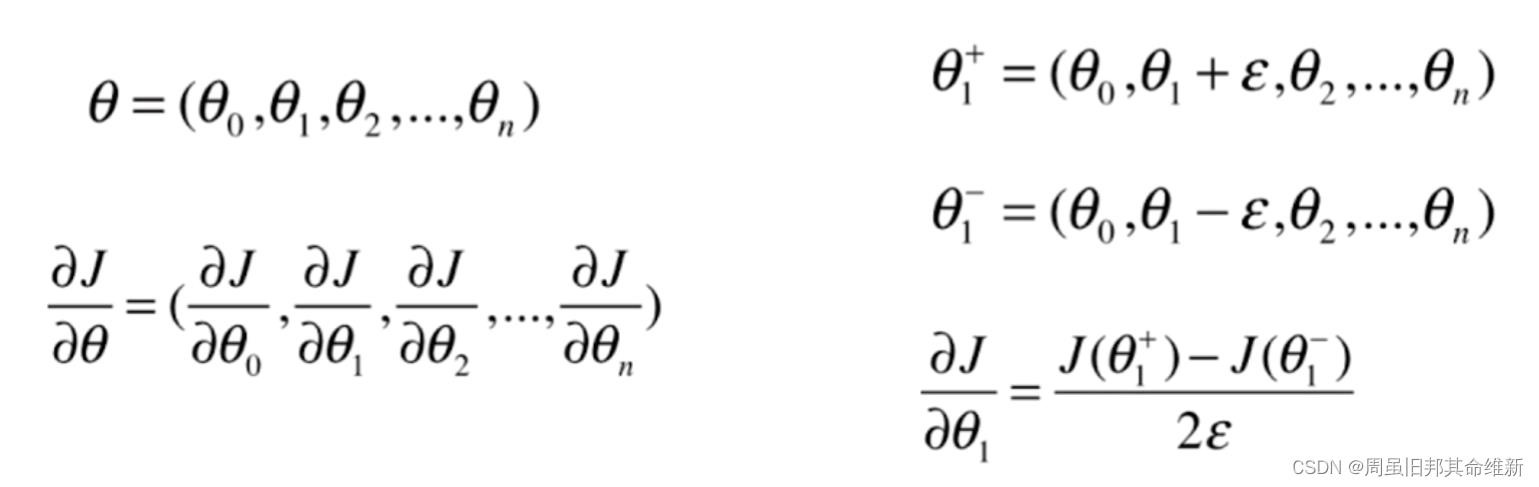
5.2 代码实现
import numpy as np
# 批量梯度下降
def gradient_descent(dJ, X_b, y, theta_init, eta, n_iters=1e4, epsilon=1e-8):
theta = theta_init
i_iter = 1
while i_iter < n_iters:
# 当前点的导数值
gradient = dJ(theta, X_b, y)
last_theta = theta
# 自变量的变化量 * 当前点的导数值 = 损失函数的变化量
# 导数的正负值代表损失函数在当前点的变化趋势是增大还是减小,因此如果导数为负则theta增加,损失函数趋于变小
# 如果导数为正,则theta减小,损失函数趋于变小,因此theta减去导数值,损失函数趋于变小
# 在eta合适的情况下,随着循环进行,导数值逐渐趋近0,eta是常数,损失函数的变化量会越来越小
theta = theta - eta * gradient
# abs求绝对值
if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
break
i_iter += 1
return theta
# 随机梯度下降
def sgd(X_b, y, theta_init, n_iters=1e4):
t0 = 5
t1 = 50
# 返回学习率(eta),随循环次数减少
def learn_rate(t):
return t0/(t + t1)
theta = theta_init
for cur_iter in range(n_iters):
# 每次迭代抽取一个样本计算导数值
rand_i = np.random.randint(0, len(X_b))
gradient = dJ_sgd(theta=theta, X_b_i=X_b[rand_i], y_i=y[rand_i])
# 即1.1代码中的theta变化方式theta = theta - eta * gradient
theta = theta - learn_rate(cur_iter) * gradient
return theta
# 原函数
def J(theta, X_b, y):
return np.sum(((y - X_b.dot(theta)) ** 2)) / len(X_b)
# 导函数
def dJ(theta, X_b, y):
return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(X_b)
def dJ_debug(theta, X_b, y, epsilon=0.01):
res = np.empty(len(theta))
for i in range(len(theta)):
theta1 = theta.copy()
theta2 = theta.copy()
theta1[i] += epsilon
theta2[i] -= epsilon
# 2*epsilon必须用括号包起来,否则就不是除以2倍的epsilon而是除以2乘以epsilon
res[i] = (J(theta1, X_b=X_b, y=y) - J(theta2, X_b=X_b, y=y))/(2*epsilon)
return res
# 返回某一个样本的导数值
def dJ_sgd(theta, X_b_i, y_i):
return X_b_i.T.dot(X_b_i.dot(theta) - y_i) * 2.
测试代码:
import numpy as np
from gradient_descent import gradient_descent
from gradient_descent import dJ_debug
m = 100000
x = np.random.normal(size=m)
X = x.reshape(-1,1)
y = 2. * x + 5. + np.random.normal(0, 3, size=m)
X_b = np.hstack([np.ones(shape=(len((X)), 1)), X])
theta_init = np.zeros(X_b.shape[1])
eta = 0.01
print(gradient_descent(dJ=dJ_debug,X_b=X_b, y=y, theta_init=theta_init, eta=eta))
5.3 总结
1、dJ_debug的方式是可以使用的,是可以得到正确结果的,只不过速度比较慢
2、dJ_debug函数其实是与J函数无关的,适用于所有的函数,dJ_debug函数完全是可以复用的而dJ_math只适用于当前任务中对应的特定的损失函数J
3、如果机器学习算法涉及到梯度的求法的时候,我们完全可以先使用dJ_debug这个函数作为梯度的求法,通过这个方式。我们先得到机器学习算法的正确结果,然后再推导公式求出来该梯度计算相应的数学界解,之后将该数学解代入到机器学习算法中,可以通过最终得到的结果和使用dJ_debug得到的结果是否一样来验证我们推导的数学解是否是正确的
以上是关于梯度下降法学习笔记的主要内容,如果未能解决你的问题,请参考以下文章