动作捕捉，系数转换，IK 等整理总结

Posted 2022-11-26 长虹剑

bvh 数据格式介绍

bvh 内部没给坐标系，应该就是按照 opengl 的坐标系
bvh 如果写的旋转是 X Y Z ，那么就是先按照Z旋转，然后再按照Y，最后X， 这部分的看出是按照这个代码来的， 当然也可一把代码理解为大写的XYZ是内旋转，按照写的顺序摆放旋转矩阵。
https://www.cxyzjd.com/article/o87481299/7690954

enum  ZYX = 1, YZX = 2, ZXY = 3, XZY = 5, YXZ = 6, XYZ = 7;
unsigned char BVH::getFlags()

	return (unsigned char)((*p - 'X' + 1)*1 + (*(p+10) - 'X' + 1)*2 + (*(p+20) - 'X' + 1)*4 - 10);

//绘制函数的核心 递归的绘制 
void BVH::drawRecursive(BVHJoint* r)

	glPushMatrix();
	//要先平移后旋转（被debug3）
	//平移 根据父节点空间
	glTranslatef(r->x,r->y,r->z);
	//根据motion中的信息和节点的通道类型进行旋转
	roateSpace(r->flags);
	//画出点
	glutSolidSphere(1.0f,20,16);
	//递归绘制子节点
	for(int i = 0; i < r->childNum; i++)
	
		drawRecursive(r->getChild(i));
	 
	glPopMatrix();

void BVH::roateSpace(unsigned char flags)

	//enum ZYX = 1, YZX = 2,ZXY = 3,XZY = 5,YXZ = 6,XYZ = 7;
	switch (flags)
	
	case ZYX: // 1 = 11 - 10, 11 = 3*1 + 2*2 + 1*4 ==> 'ZYX'
		glRotatef(pFrame[0],0.0f,0.0f,1.0f);
		glRotatef(pFrame[1],0.0f,1.0f,0.0f);
		glRotatef(pFrame[2],1.0f,0.0f,0.0f);
		break;
    case XYZ: // ==> 'XYZ'
		glRotatef(pFrame[0],1.0f,0.0f,0.0f);
		glRotatef(pFrame[1],0.0f,1.0f,0.0f);
		glRotatef(pFrame[2],0.0f,0.0f,1.0f);
		break;
		// omit 
	

反向动力学（IK）的一些资料

给定3D/2D顶点如何求出骨骼旋转系数

方法一：
深度学习的方法，训练一个3D点到旋转系数的网络

方法二：
最优化的方法，不过最优化需要有初始值，最好能有个网路可以给出初始值，这样优化快一点。关于这一点可以看一个网络 IKNET
最优化其实也有几种思路，一般最优化的条件都是重建项+先验项（这里主要防止解出不合适的骨骼结构，可以加混合高斯先验项）
1）可以使用梯度下降 smplify-x ，这个SPIN
2）可以数值求解雅克比，例子在 Minimal-IK
3）C++ 雅克比解析求解，可以用 MonocularTotalCapture
具体在这里

bool AdamFullCost::Evaluate(double const* const* parameters,
        double* residuals,
        double** jacobians) const

常规的解法

CCD： 就是给定目标点的位置，并且确定好影响的骨骼数目，则依次让旋转靠近目标点即可
基于优化的方法： 拆成 欧拉角，并且再拆成三个角度分别求
逆雅可比矩阵： 主要是希望雅可比矩阵不用变，求解的快

关于 CCD
主要是考虑让末端点对齐到目标上，这里解释一段code，来自 逆运动学IK

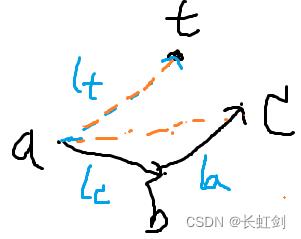
a b c 是链式骨骼，t 是给定目标点，让c 靠近， 后面一点有点看不懂

void two_joint(
    glm::vec3 a, glm::vec3 b, 
    glm::vec3 c, glm::vec3 t, float eps, 
    glm::mat4& a_pR, glm::mat4& b_pR,
    glm::mat4& a_gR, glm::mat4& b_gR,
    glm::mat4& a_lR, glm::mat4& b_lR) 
    
    float lc = glm::length(b - a);
    float la = glm::length(b - c);
    float lt = glm::clamp(glm::length(t - a), eps, lc + la - eps);
    
    if (glm::length(c - t) < eps)  return; 
	
	// 上面就是求长度，注意是长度并不是向量，接着利用余弦公式，求一些夹角的值
    float ac_ab_0 = acosf(glm::clamp(glm::dot(glm::normalize(c - a), glm::normalize(b - a)), -1.0f, 1.0f));
    float ba_bc_0 = acosf(glm::clamp(glm::dot(glm::normalize(a - b), glm::normalize(c - b)), -1.0f, 1.0f));
    float ac_at_0 = acosf(glm::clamp(glm::dot(glm::normalize(c - a), glm::normalize(t - a)), -1.0f, 1.0f));
    
    // 这里利用的是三角形余弦公式，注意，这里第一个是假设 t 与 c 已经重合，这样夹角 cab 与 abc 必然会改变，这里就是算出最终的角度是多少
    float ac_ab_1 = acosf(glm::clamp((la*la - lc*lc - lt*lt) / (-2*lc*lt), -1.0f, 1.0f));
    float ba_bc_1 = acosf(glm::clamp((lt*lt - lc*lc - la*la) / (-2*lc*la), -1.0f, 1.0f));
    
    // 这里主要是构造一个旋转轴，因为要在平面按这个法向量旋转，
    glm::vec3 a0 = glm::normalize(glm::cross(b - a, c - a));
    glm::vec3 a1 = glm::normalize(glm::cross(t - a, c - a));
    
    glm::mat3 r0 = glm::mat3(glm::rotate(ac_ab_1 - ac_ab_0, -a0));
    glm::mat3 r1 = glm::mat3(glm::rotate(ba_bc_1 - ba_bc_0, -a0));
    glm::mat3 r2 = glm::mat3(glm::rotate(ac_at_0,           -a1));
    
    glm::mat3 a_lRR = glm::inverse(glm::mat3(a_pR)) * (r2 * r0 * glm::mat3(a_gR)); 
    glm::mat3 b_lRR = glm::inverse(glm::mat3(b_pR)) * (r1 * glm::mat3(b_gR)); 
    
    for (int x = 0; x < 3; x++)
    for (int y = 0; y < 3; y++) 
      a_lR[x][y] = a_lRR[x][y];
      b_lR[x][y] = b_lRR[x][y];
    
    
  

还有一个是 https://its401.com/article/jiangcaiyang123/14047265
这个只写了一个骨骼的情况，其实是类似的，主要就是旋转要在局部坐标系下。
角度就有反三角，轴向就用叉积，就获得了。

一些比较好的项目

VPOSE 可以支持系数预测，判断姿态的好坏等