高级数据结构—二项堆与斐波那契堆详细介绍(算法导论中科大USTC)
Posted 之墨_
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了高级数据结构—二项堆与斐波那契堆详细介绍(算法导论中科大USTC)相关的知识,希望对你有一定的参考价值。

二项堆与斐波那契堆
斐波那契堆请点击这里👈
数据结构与堆
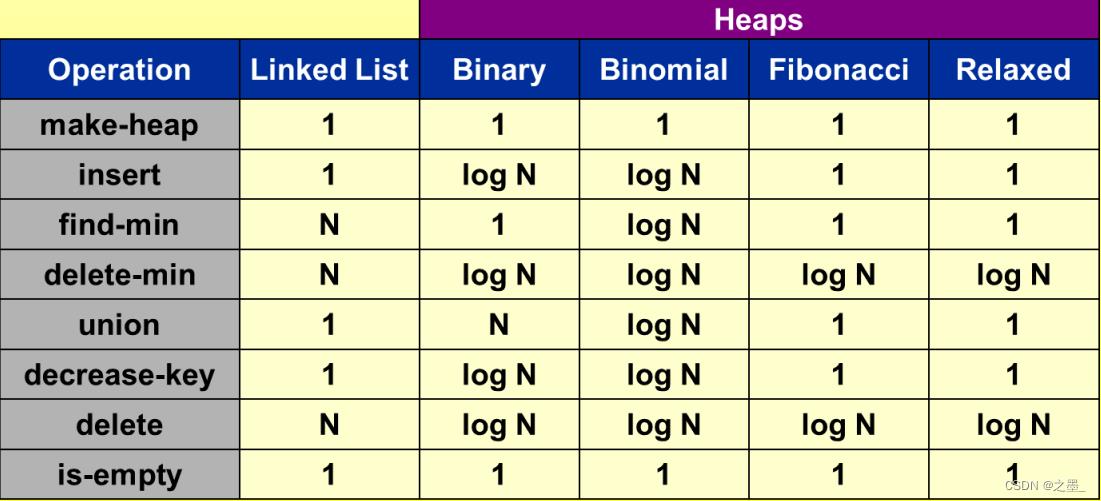
下图列出了小顶堆在各种数据结构(链表、二叉堆、二项堆、斐波那契堆、松弛堆)的实现下,各种基本操作的时间复杂度
二项树
二项堆是二项树的集合。在了解二项堆之前,先对二项树进行介绍。
定义
二项树是一种递归定义的有序树。它的递归定义如下:
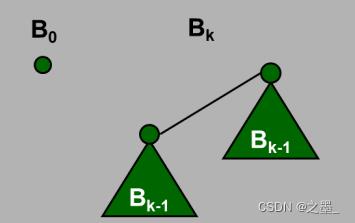
- 二项树 B 0 B_0 B0只有一个结点
- 二项树
B
k
B_k
Bk由两棵二项树
B
(
k
−
1
)
B_(k-1)
B(k−1)组成的,其中一棵树是另一棵树根的最左孩子
性质
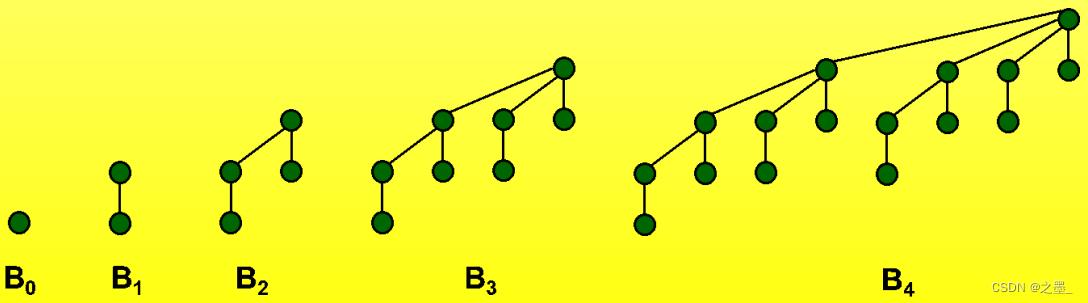
[性质一]
B
k
B_k
Bk共有
2
k
2^k
2k个节点。
如上图所示,
B
0
B0
B0有
2
0
=
1
2^0=1
20=1节点,
B
1
B_1
B1有
2
1
=
2
2^1=2
21=2个节点,
B
2
B_2
B2有
2
2
=
4
2^2=4
22=4个节点,…
[性质二]
B
k
B_k
Bk的高度为
k
k
k。
如上图所示,
B
0
B_0
B0的高度为
0
0
0,
B
1
B_1
B1的高度为
1
1
1,
B
2
B_2
B2的高度为
2
2
2,…
[性质三]
B
k
B_k
Bk在深度
i
i
i处恰好有
C
(
k
,
i
)
C(k,i)
C(k,i)个节点,其中
i
=
0
,
1
,
2
,
.
.
.
,
k
i=0,1,2,...,k
i=0,1,2,...,k。
C
(
k
,
i
)
C(k,i)
C(k,i)是高中数学中阶乘元素,例如,
C
(
10
,
3
)
=
(
10
∗
9
∗
8
)
(
3
∗
2
∗
1
)
=
240
C(10,3)=\\cfrac(10*9*8) (3*2*1)=240
C(10,3)=(3∗2∗1)(10∗9∗8)=240
B
4
B_4
B4中深度为
0
0
0的节点
C
(
4
,
0
)
=
1
C(4,0)=1
C(4,0)=1
B
4
B_4
B4中深度为
1
1
1的节点
C
(
4
,
1
)
=
4
/
1
=
4
C(4,1)= 4 / 1 = 4
C(4,1)=4/1=4
B
4
B_4
B4中深度为
2
2
2的节点
C
(
4
,
2
)
=
(
4
∗
3
)
/
(
2
∗
1
)
=
6
C(4,2)= (4*3) / (2*1) = 6
C(4,2)=(4∗3)/(2∗1)=6
B
4
B_4
B4中深度为
3
3
3的节点
C
(
4
,
3
)
=
(
4
∗
3
∗
2
)
/
(
3
∗
2
∗
1
)
=
4
C(4,3)= (4*3*2) / (3*2*1) = 4
C(4,3)=(4∗3∗2)/(3∗2∗1)=4
B
4
B_4
B4中深度为
4
4
4的节点
C
(
4
,
4
)
=
(
4
∗
3
∗
2
∗
1
)
/
(
4
∗
3
∗
2
∗
1
)
=
1
C(4,4)= (4*3*2*1) / (4*3*2*1) = 1
C(4,4)=(4∗3∗2∗1)/(4∗3∗2∗1)=1
合计得到
B
4
B_4
B4的节点分布是
(
1
,
4
,
6
,
4
,
1
)
(1,4,6,4,1)
(1,4,6,4,1)。
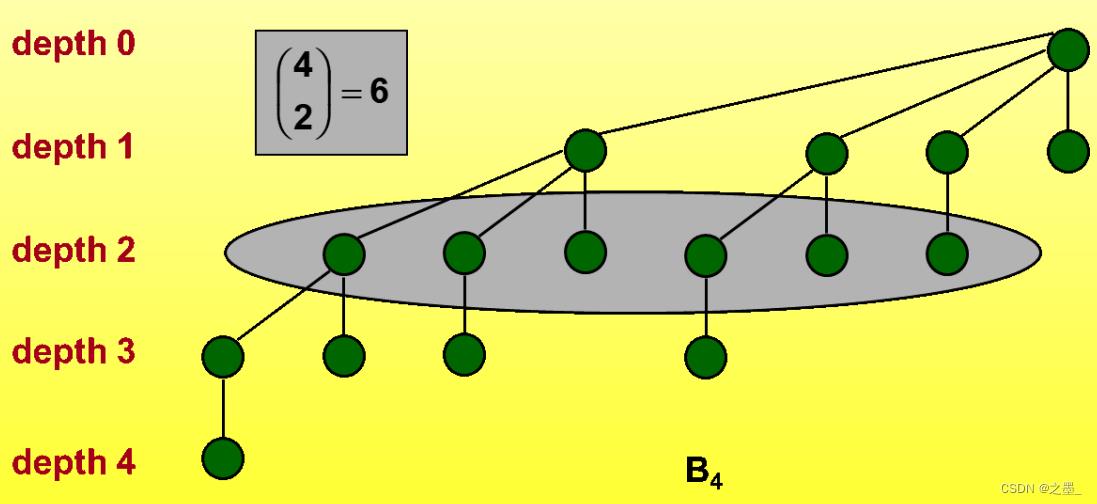
[性质四]
根的度数为
k
k
k,它大于任何其它节点的度数。
节点的度数是该结点拥有的子树的数目。
二项堆
定义
二项堆是指满足以下性质的二项树的集合:
- 每棵二项树都满足最小堆性质。即,父节点的关键字 < = <= <= 它的孩子的关键字。
- 不能有两棵或以上的二项树具有相同的度数(包括度数为
0
0
0)。换句话说,具有度数
k
k
k的二项树有
0
0
0个或
1
1
1个。

上图就是一棵二项堆,它由二项树 B 0 B_0 B0、 B 1 B_1 B1和 B 4 B_4 B4组成。对比二项堆的定义:
- 二项树 B 0 、 B 1 、 B 4 B_0、B_1、B_4 B0、B1、B4都是最小堆
- 二项堆不包含相同度数的二项树
性质
二项堆的第 1 1 1个性质保证了二项堆的最小节点就是某个二项树的根节点,第 2 2 2个性质则说明结点数为n的二项堆最多只有 log n + 1 \\logn + 1 logn+1棵二项树。实际上,将包含 n n n个节点的二项堆,表示成若干个 2 2 2的指数和(或者转换成二进制),则每一个 2 2 2个指数都对应一棵二项树。例如, 13 13 13(二进制是 1101 1101 1101)的 2 2 2个指数和为 13 = 23 + 22 + 20 13=23 + 22+ 20 13=23+22+20, 因此具有 13 13 13个节点的二项堆由度数为 3 , 2 , 0 3, 2, 0 3,2,0的三棵二项树组成。
实现
- 使用左子级、右同级指针表示树。 每个节点三个链接:父节点、左节点(最左边的子节点)、右边(右边的同级节点)。
- 与单链表相连的树根。 当我们遍历根链时,树的度数会严格增加。
内存
下图为二项式堆 H H H,堆由二元树 B 0 、 B 2 和 B 3 B_0、B_2 和B_3 B0、B2和B3组成,它们分别具有 1 、 4 和 8 1、4 和 8