DP问题从入门到精通4（状态压缩dp，蒙德里安，最短Hamilton路径）

Posted 2022-11-25 芜湖之肌肉金轮

DP问题从入门到精通系列

• DP问题入门到精通1
• DP问题入门到精通2.1
• DP问题入门到精通2.2
• DP问题入门到精通3
• DP问题入门到精通5

dp问题学到到这里理解难度可能会突然上升一个档次，但是不用担心，因为这类问题也就顶多理解起来难一点

 

而且状态压缩问题做起来其实非常有趣，做完挺有成就感的，那么就先看看蒙德里安的梦想这道题把

 

蒙德里安的梦想

蒙德里安的梦想，这道题是很经典的状态压缩的问题，首先其本质依旧是dp问题，所以我们还是要去思考如何去进行状态表示，和状态计算，在状态表示之前我们先观察一下题目，我们发现假如我们先摆横着的，那么横着的1X2的小方块摆放完之后，在合法的前提下，剩下的地方用竖着的方块摆放就只有一种方法。所以方法是   横着的X1就是该状态下的总方法数

 

所以我们可以确定思考的方向是横着开始摆放，所以状态表示可以写成，f[ i , j ]:方块前i-1列伸到 i 的状态数量 j 。

比如 f[ 2, 010 ]

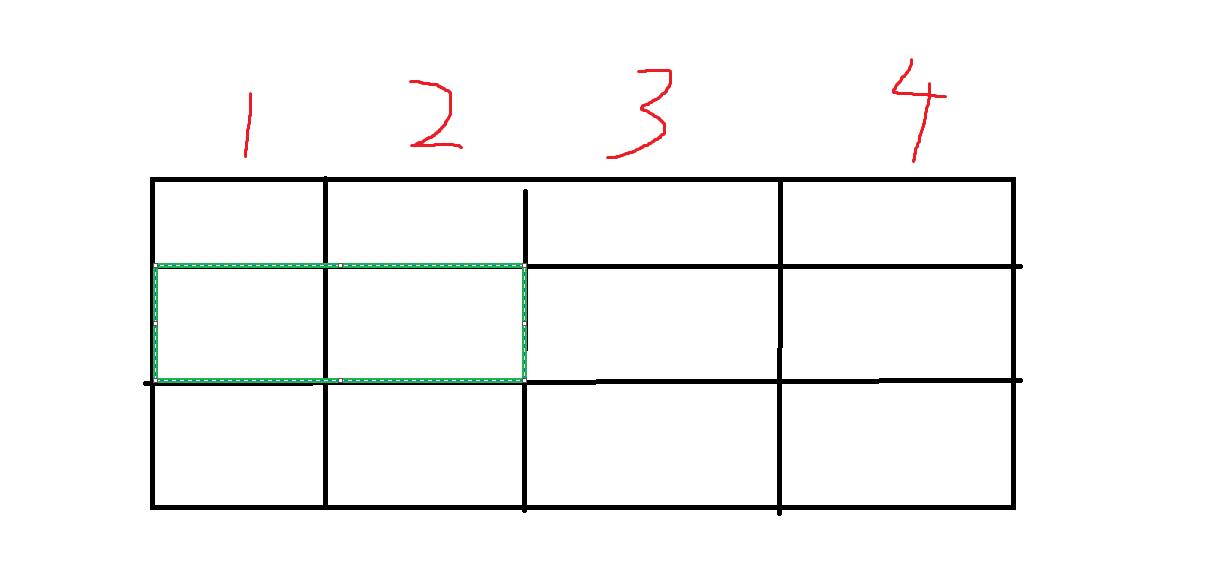
那么接下来在更新，进行状态计算之前我们需要什么，进行合法状态的判断

首先根据我们的状态表示，假如 i - 2 有 00100这个状态 

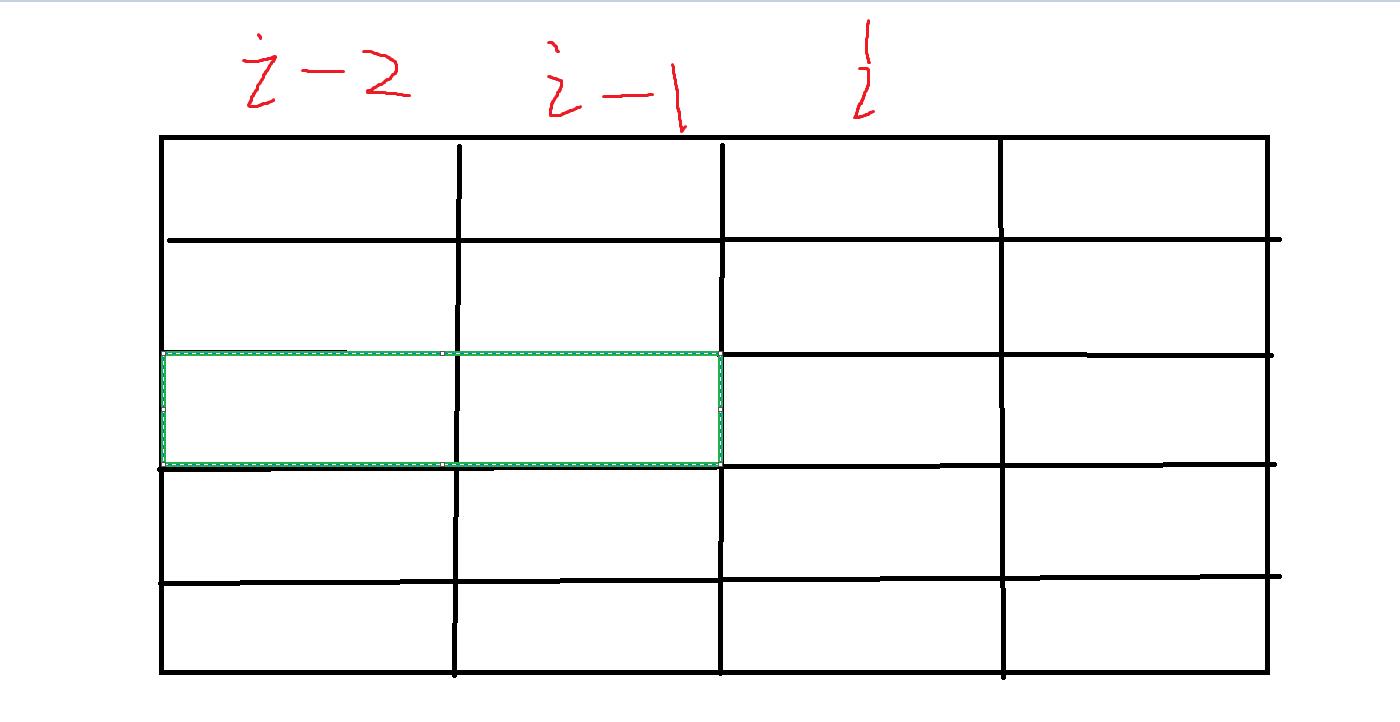
 那么如果i - 1 也有 00100这个状态 

 就会有蓝色的冲突状态，所以 j & k == 0 （假设 j 是 i - 1的状态，k是 i - 2）

还有什么会影响到状态的合法性？当从 i - 2伸到 i - 1 ，和i -1 伸到 i 的状态摆放完之后，i - 1列的连续空位必须是偶数，因为我们放的是1X2的小方块，竖着放的话就是2X1的，所以连续的空位必须是偶数才能放下。

const int N=12,M=1<<N;

long long f[N][M];
int n,m;
vector<int> state[M];//储存合法状态
bool st[N];判断该状态是否合法
cin>>n>>m;
for(int i=0;i<1<<n;i++)//枚举每一个状态

    int cnt=0;//计算0的数量（空位是否是偶数）
    bool is_vaild=true;
    for(int j=0;j<n;j++)
        if(i >> j & 1)
        
            if(cnt&1)
            
                is_vaild=false;
                break;
            
            cnt=0;
        
        else cnt++;
        if(cnt&1)is_vaild=false;
        st[i]=is_vaild;

for(int i=0;i<1<<n;i++)

    state[i].clear();
    for(int j=0;j<1<<n;j++)
        if(( i & j ) == 0 && st[ i | j ])//st[ i | j ]表示去找有偶数个空位的合状态
        state[i].push_back(j);

 接下来就是状态计算因为 f[ i , j ]:方块前 i - 1 列伸到 i 的状态数量 j 。所以我们可以累加到 m 

最后 答案 f [ m , 0 ]表示，m-1列已经摆好，且伸到 m 的方块数为0，这样子剩下的 m 可以全部用竖着的摆满，所以这个状态就是我们的状态表示所对应的答案：

#include<iostream>
#include<algorithm>
#include<vector>
#include <cstring>
using namespace std;

const int N=12,M=1<<N;

long long f[N][M];
int n,m;
vector<int> state[M];
bool st[N];

int main()

    while(cin>>n>>m,n||m)
    
        for(int i=0;i<1<<n;i++)
        
            int cnt=0;
            bool is_vaild=true;
            for(int j=0;j<n;j++)
                if(i >> j & 1)
                
                    if(cnt&1)
                    
                        is_vaild=false;
                        break;
                    
                    cnt=0;
                
                else cnt++;
            if(cnt&1)is_vaild=false;
            st[i]=is_vaild;
        
         for(int i=0;i<1<<n;i++)
        
            state[i].clear();
            for(int j=0;j<1<<n;j++)
            if((i&j)==0&&st[i|j])
                state[i].push_back(j);
        
    memset(f,0,sizeof(f));
    f[0][0]=1;
    for(int i=1;i<=m;i++)
        for(int j=0;j<1<<n;j++)
            for(auto k :state[j])
                f[i][j]+=f[i-1][k];
                
    cout<<f[m][0]<<endl;
    
    
  
    
    return 0;

 总结一下状态压缩其实，就是把方案压缩成二进制，用一个数去唯一的表示一种方案，从而达到一个压缩的目的，那么现在就趁热去看看下一个比较经典的状态压缩dp。

 

 最短Hamilton路径

这个问题是一个NP难问题，也是图论的一种思想，意思是你无法在一个多项式的时间内求出问题的值，这其实就说明，我们基本上无法使用现在的算法将其优化到多项式的时间，所以我们应该往暴力的方向去想，比如暴搜？

 

我们可以看出数据范围是20，暴力的话就是20的阶乘也就是2*10^18次方数据量非常的大所以一定会超时，那么我们应该怎么去想这种问题的，首先我们要想，这道题我到底应该关注什么——其实也就是状态表示，根据题意，我们是要从0走到n-1且最短，深搜的话，我们会把 

 

2->1->3

1->2->3

 

都搜一遍，但其实我们根本不关注我到的点的顺序，我只关心，我已经走过哪些点了，和我走现在停在哪里，那么这么一想，其实问题就简单多了

 

我可以列出这样的状态方程f [ i , j ],表示 i 中所有的状态都最后停在了 j

那么这个状态应该由什么转移过来呢？

它可以由所有没有到过  j  的集合中转移过来

我们用二进制表示 i 去枚举每一个状态 1 表示走过 0 表示没有走过。

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

const int N = 20,M=1<<N;
int f[M][N];

int weight[N][N];
int n;

int main()

    cin>>n;
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
            cin>>weight[i][j];
            
    memset(f,0x3f,sizeof f);
    f[1][0]=0;//根据题目要求我们一开始在0号点，所有我们在0这个位置是走过了，二进制表示就是000001，所以是1，且距离是0
    for(int i=0;i<1<<n;i++)
        for(int j=0;j<n;j++)
            if(i >> j & 1 )//看看是否走到了 j 
                for(int k=0;k<n;k++)
                    if(i-(1 << j) >> k & 1)//排除 j 且看看 是否走到了 k 
                        f[i][j]=min(f[i][j],f[i-(1<<j)][k]+weight[k][j]);
    cout<<f[(1<<n)-1][n-1];    
    return 0;    

状态压缩类DP结束

刚开始学习的时候感觉有点晕晕的，这可能跟我对二进制不敏感有关，但是当我发现，010100，这样的0和1可以用来唯一的表示一种状态的时候，我深深的被吸引了，哈哈哈，这些其实不难，只要慢下来慢慢学不但能学懂，还能收获快乐，希望我上面的见解可以帮助到大家

学习网站（acwing）