算法笔记：冒泡排序

Posted 2022-11-25 UQI-LIUWJ

1 最基本的冒泡排序

冒泡排序（Bubble Sort）是排序算法里面比较简单的一个排序。它重复地遍历要排序的数列，一次比较两个数据元素，如果顺序不对则进行交换，并一直重复这样的走访操作，直到没有要交换的数据元素为止。

1.1 算法举例

• 比如有一个序列：1、5、4、2、6、3，我们要将它按从小到大排序。

• 按照冒泡排序的思想，我们要把相邻的元素两两比较，根据大小来交换元素的位置

轮次	操作内容
第一轮 （右边每一格是一小步）	比较1和5，1比5小，顺序正确，元素位置不变 1 5 4 2 6 3
	比较5和4，5比4大，顺序错误，交换元素位置 1 5 4 2 6 3  ——> 1 4 5 2 6 3
	比较5和2，5比2大，顺序错误，交换元素位置 1 4 5 2 6 3 ——> 1 4 2 5 6 3
	比较5和6，5比6小，顺序正确，元素位置不变 1 4 2 5 6 3
	比较6和3，6比3大，顺序错误，交换元素位置 1 4 2 5 6 3 ——> 1 4 2 5 3 6
第二轮	比较1~3即可，因为最后的6已经是有序的了 最后的结果是 1 2 4 3 5 6
第三轮	比较1~3 即可，因为最后的5，6已经是有序的了 最后的结果是 1 2 3 4 5 6
第四轮	比较1~3即可，因为最后的4、5、6已经是有序的了 最后的结果是 【注意这一轮没有任何更新！也就是说，第四轮是没有作用的轮次！】 1 2 3 4 5 6
第五轮	比较1~2即可，因为后面的都是有序的了 最后的结果是 【注意这一轮没有任何更新！也就是说，第四轮是没有作用的轮次！】 1 2 3 4 5 6

 1.2 代码实现（python）

lst=[1,5,4,2,6,3]


for i in range(len(lst)):
    for j in range(len(lst)-i-1):
        #i 表示多少个元素已经排序好了,一开始是0个，最终是len-1个，也即i＜len
        
        #每一步是j和j+1 进行比较，所以j+1的范围是：j+1 <len-i，也即j<len-i-1
        
        if(lst[j]>lst[j+1]):
            tmp=lst[j+1]
            lst[j+1]=lst[j]
            lst[j]=tmp
            #如果比较的两个元素顺序错误，那么交换两个元素的顺序
            
lst
# [1, 2, 3, 4, 5, 6]

2  算法优化1（添加已排序标记）

• 从1.1的表格我们不难发现，当第三轮结束的时候，其实已经排序好了。第四第五轮是冗余的遍历。我们可以考虑将其去掉。
• 在这里，我们创立一个“已排序”标记。如果在某一轮，没有发生一次换位，那么说明所有元素都已经排序完成，那么就可以结束算法了
• 比如上图，在第四轮的过程中，发现已经没有顺序的交换了，所以结束算法。

2.1 代码实现（python）

lst=[1,5,4,2,6,3]


for i in range(len(lst)):
    flag_over=True
    #表示某一轮是否已经全部排序完成
    #如果有元素交换，那么flag_over应该是False，如果没有元素交换，那么flag_over会一直是True
    for j in range(len(lst)-i-1):
        #i 表示多少个元素已经排序好了,一开始是0个，最终是len-1个，也即i＜len
        
        #每一步是j和j+1 进行比较，所以j+1的范围是：j+1 <len-i，也即j<len-i-1
        
        if(lst[j]>lst[j+1]):
            tmp=lst[j+1]
            lst[j+1]=lst[j]
            lst[j]=tmp
            #如果比较的两个元素顺序错误，那么交换两个元素的顺序
            flag_over=False
            #发生了元素交换，说明至少在这一轮，整个序列还没有排序完成
    
    if(flag_over==True):
        break
            
            
lst
#[1, 2, 3, 4, 5, 6]

3 算法优化2（每次不一定只往前一格）

• 有的情况下，一轮结束了，可能末尾好几个点都排序好了，那么再一轮一轮地遍历这些点也是不合适的，所以优化方向2是记录一下某一轮最后一个没有排序好的点的位置
• 改进方法是，每次交换后，记录一下交换的位置。每轮最后一个交换的位置就是下一次lst[j]需要遍历到的最后一个位置【因为后面的位置都没有发生交换了，也就是已经排序完成了】

3.1 代码实现

lst=[1,5,4,2,6,3]


for i in range(len(lst)):
    flag_over=True
    #表示某一轮是否已经全部排序完成
    #如果有元素交换，那么flag_over应该是False，如果没有元素交换，那么flag_over会一直是True
    
    j_end_index=len(lst)-i-1
    #每一轮比较的j坐标的末尾坐标
    
    tmp_j_end=0
    
    for j in range(j_end_index):
        #i 表示多少个元素已经排序好了,一开始是0个，最终是len-1个，也即i＜len
        
        #每一步是j和j+1 进行比较，所以j+1的范围是：j+1 <len-i，也即j<len-i-1
        
        if(lst[j]>lst[j+1]):
            tmp=lst[j+1]
            lst[j+1]=lst[j]
            lst[j]=tmp
            #如果比较的两个元素顺序错误，那么交换两个元素的顺序
            flag_over=False
            #发生了元素交换，说明至少在这一轮，整个序列还没有排序完成
            
            tmp_j_end=j
            #每一次交换后，记录一下发生交换的位置
        
    j_end_index=tmp_j_end
    #这一轮最后一次交换所在的位置，就是下一轮j需要遍历到的位置
    #因为后续位置的元素都已经排序完成了
    
    if(flag_over==True):
        break
            
            
lst
#[1, 2, 3, 4, 5, 6]

实现了j_end_index之后，甚至flag_over都不用了。因为如果某一轮内没有发生交换，那么tmp_j_end就是默认的0，那么下一轮j的取值范围就是range(0)，空集合

4 冒泡排序复杂度

4.1 时间复杂度

---

• 最差时间复杂度：元素正好倒序，每一轮只能少遍历一个元素，复杂度是
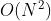
• 最好时间复杂度：元素正序，一轮搞定，复杂度O(N)

4.2 空间复杂度

只需要一个进行元素交换的额外空间，复杂度是O(1)