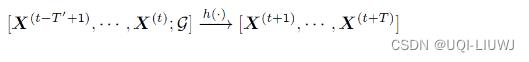论文笔记：DCRNN （Diffusion Convolutional Recurrent Neural Network: Data-Driven Traffic Forecasting）

Posted 2022-11-25 UQI-LIUWJ

ICLR 2018

0 abstract

• 交通预测是一项具有挑战的任务
  • 对道路网络的复杂空间依赖性
  • 随道路条件变化的非线性时间动态
  • 长期预测的固有困难
• ——>将交通流建模为有向图上的扩散过程
• ——>引入扩散卷积递归神经网络 (DCRNN)

  • 使用图上的双向随机游走来捕获空间依赖性

  • 使用具有计划采样（scheduled sampling）的编码器-解码器架构来捕获时间依赖性

1 introduction

1.1  交通预测的挑战性

• 复杂的时空依赖性+长期预测的固有困难
  • 交通时间序列表现出强烈的时间动态。
  • 高峰时间或事故等可能会导致非平稳性，从而难以长期预测。
  • 道路网络上的传感器包含复杂而独特的空间相关性
    • road1和road2 同向相邻，所以他们的交通流量很相近
    • road1和road3尽管在欧几里得空间中相近，但由于是反向的，所以交通流量并不接近
    • ——>交通中的空间结构是非欧式的和定向的

 1.2 本文贡献

• 使用有向图表示交通传感器之间的成对空间相关性，其节点是传感器，边权重表示通过道路网络距离测量的传感器对之间的接近度。
• 将交通流的动态建模为扩散过程，并提出扩散卷积操作来捕获空间依赖性。
• 进一步提出了扩散卷积递归神经网络（DCRNN）
  • 扩散卷积（diffusion convolution）
    • ——>具有直观的解释
    • ——>可以有效的进行计算
  • seq2seq架构
  • 计划采样（scheduled sampling）

2 方法

2.1 交通预测问题定义

• 交通预测的目标是根据道路网络上 N 个相关传感器先前观察到的交通流量来预测未来的交通速度。
• 将传感器网络表示为加权有向图
  •  V 是一组节点 |V| = N
  • E 是一组边
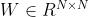  • 是一个加权邻接矩阵，表示节点的接近度（eg,它们距离的函数）。
•  将上观察到的交通流表示为图信号
  •  P 是每个节点的特征数。
•  令 X(t) 表示在时间 t 观察到的图信号，交通预测问题旨在给定图 G的情况下，学习一个函数 h(·)，将 T’ 个历史图信号映射到未来 T 个图信号
  • 

 2.2 空间依赖性

• 将交通流与扩散过程相关联来对空间依赖性进行建模，该扩散过程明确地捕捉了交通动态的随机性。

   

  • 这种扩散过程的特点是 G 上的随机游走
    • 重启概率为 α ∈ [0, 1]（1-α的概率随机游走到邻居节点，α的概率回到起始点）
    • 转移矩阵

       

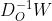
      • 是出度对角矩阵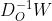
      • 就是转移到不同邻居点的概率

 

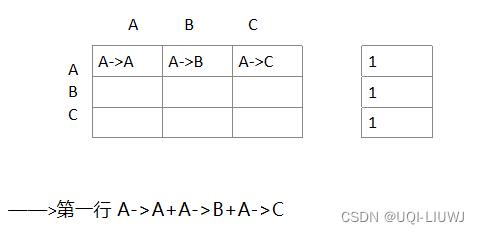
• • 经过多步时间步之后，这种马尔可夫过程将收敛到一个平稳分布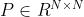，其中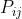是从节点i转移/扩散到节点j的概率
    • 扩散过程的平稳分布可表示为图上无限随机游走的加权组合，并以封闭形式计算
    • 
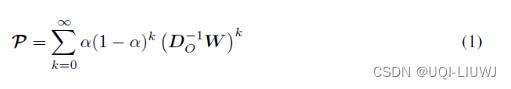
    • 其中k是扩散步骤
    • 在实践中，使用扩散过程的有限 K 步截断，并为每个步骤分配可训练的权重。
    • 同时，还包括反向扩散过程，这样双向扩散为模型提供了更大的灵活性来捕捉来自上游和下游流量的影响。

2.2.1 扩散卷积

• 所以扩散卷积定义为

   

  • 
  • 其中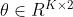是滤波器参数，分别是正向扩散过程和反向扩散过程的转移矩阵
  • 一般来说，计算卷积比较昂贵，是的时间复杂度。但如果G是稀疏的，那么可以使用时间复杂度的稀疏矩阵乘法（每个稀疏矩阵乘法是O(E)的复杂度）

2.2.2 扩散卷积层

 使用等式 2 中定义的卷积运算，我们可以构建一个扩散卷积层，将 P 维特征映射到 Q 维输出

参数Θ此时的维度是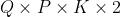。其中参数化了第p个输入和第q个输出之间的卷积滤波器

所以扩散卷积层为（输入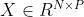，输出)：

这里α是激活函数

2.3 时间依赖性 

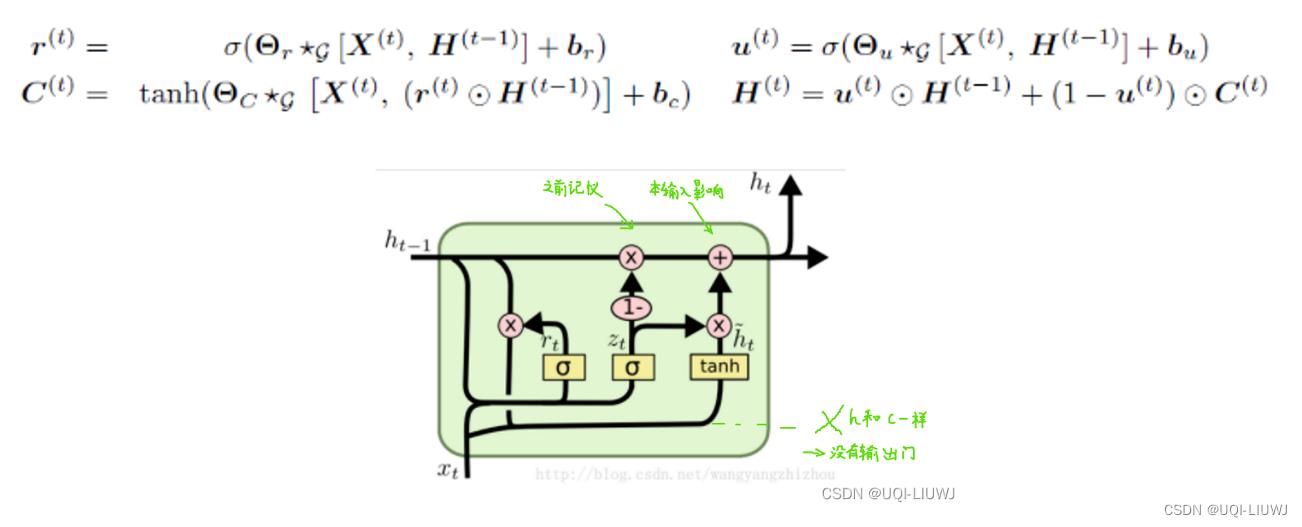
• 利用循环神经网络 (RNN) 对时间依赖性进行建模——使用门控循环单元
• 这里将GRU种的矩阵乘法替换为扩散卷积

2.4 计划采样 

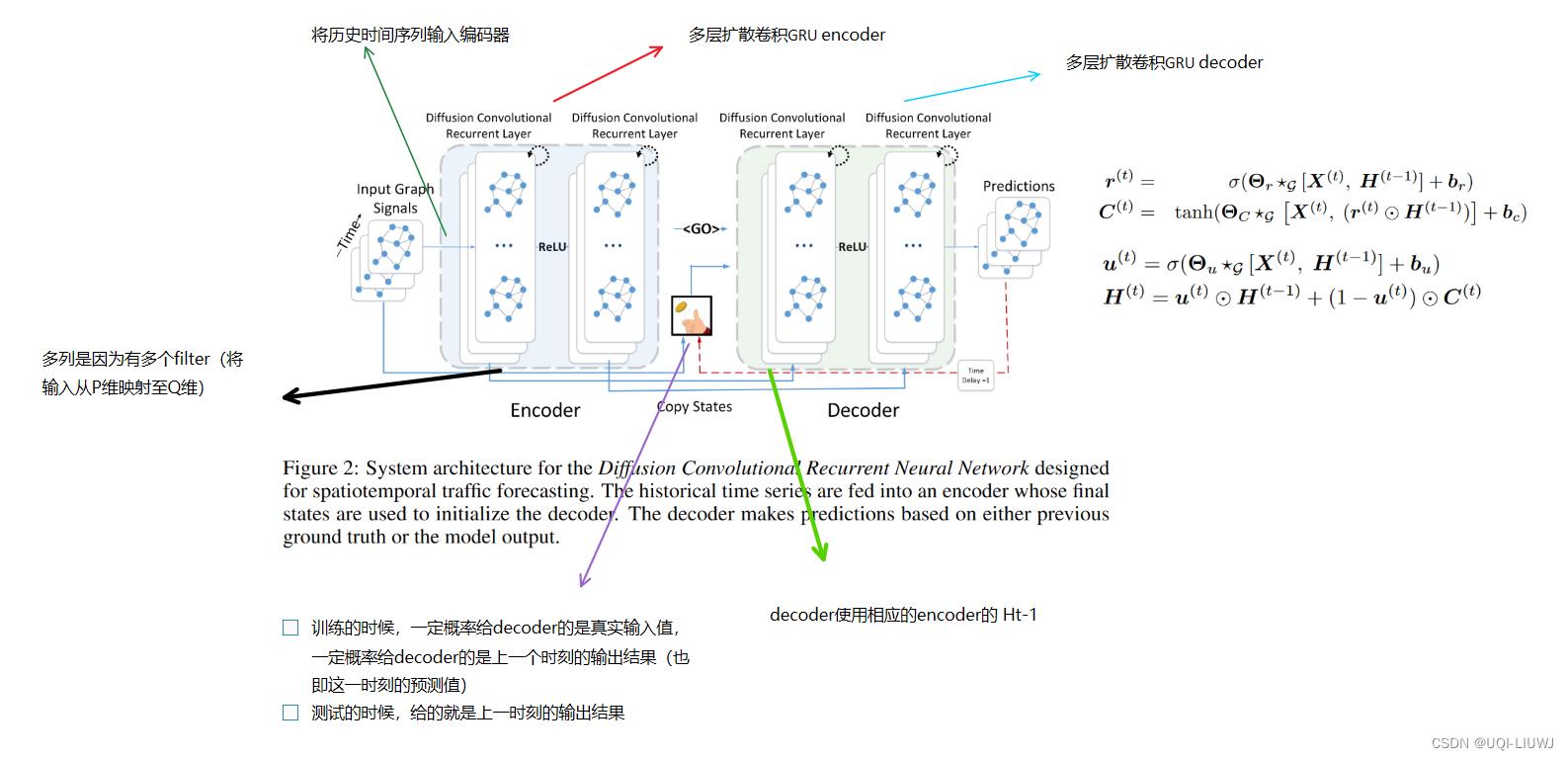
• 在多步超前预测中，这里采用seq2seq架构。
  • 编码器和解码器都是带有 DCGRU 的循环神经网络。
• 在训练期间，我们将历史时间序列输入编码器，并使用其最终状态来初始化解码器。解码器在给定先前的真实值的情况下生成预测。
• 在测试时，真实值被模型本身生成的预测所取代。
• 训练和测试的输入分布之间的差异会导致性能下降。
  • 为了缓解这个问题，我们将计划抽样 集成到模型中，在该模型的第 i次迭代中，我们向模型提供概率为 ϵi的真实值或概率为 1 - ϵ i 的模型的预测。在训练过程中，ϵ i逐渐减小到 0，让模型学习测试分布。

 

3 实验部分

3.1 数据集

• METR-LA
  • 该交通数据集包含洛杉矶环路检测器收集的交通信息。
  • 这里选择了 207 个传感器并收集了 2012 年 3 月 1 日至 2012 年 6 月 30 日 4 个月的数据进行实验。 
• PEMS-BA Y
  • 在湾区选择了 325 个传感器，并收集了 2017 年 1 月 1 日至 2017 年 5 月 31 日 6 个月的数据进行实验。
• 在这两个数据集中，作者将交通速度读数汇总到 5 分钟的窗口中，并应用 Z-Score 标准化。 70% 的数据用于训练，20% 用于测试，其余 10% 用于验证。
• 为了构建传感器图，作者计算传感器之间的成对道路网络距离，并使用阈值高斯核构建邻接矩阵 

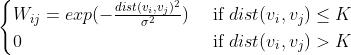
σ是举例的标准差，K是阈值

 

3.2 baseline

1）HA：Historical Average，将交通流量建模为季节性过程，使用前几季的加权平均值作为预测；
2）ARIMAkal：具有卡尔曼滤波器的自回归综合移动平均模型；
3）VAR：向量自回归。
4）SVR：Support Vector Regression，使用线性支持向量机进行回归任务；
5）前馈神经网络 (FNN)：具有两个隐藏层和 L2 正则化的前馈神经网络。
6）具有全连接的 LSTM 隐藏单元的递归神经网络 (FC-LSTM) 
 

所有基于神经网络的方法都是使用 Tensorflow  实现的，使用Adam进行训练。

3.3 实验结果

 

• 表 1 显示了不同方法在两个数据集上提前 15 分钟、30 分钟和 1 小时预测的比较。这些方法基于流量预测中的三个常用指标进行评估， (1) 平均绝对误差 (MAE)、(2) 平均绝对百分比误差 (MAPE) 和 (3) 均方根误差 (RMSE)。在计算这些指标时会排除缺失值。
• 
• 我们在这两个数据集中观察到以下现象。
  • (1) 基于 RNN 的方法，包括 FC-LSTM 和 DCRNN，通常优于其他强调时间依赖性建模重要性的基线。
  • (2) DCRNN 在所有预测范围的所有指标上都取得了最佳性能，这表明了时空依赖建模的有效性。
  • (3) 基于深度神经网络的方法，包括 FNN、FC-LSTM 和 DCRNN，对于长期预测，例如提前 1 小时，往往比线性基线具有更好的性能。这是因为时间依赖性随着地平线的增长而变得越来越非线性。此外，由于历史平均法不依赖于短期数据，因此其性能不受预测范围内的小幅增长的影响。

 

在 METR-LA（以复杂交通状况而闻名的洛杉矶）数据集上的交通预测比 PEMS-BAY（湾区）数据集中的交通预测更具挑战性。因此，我们使用 METR-LA 作为后续实验的默认数据集。
 

3.4 空间依赖性建模的影响

为了进一步研究空间依赖建模的效果，我们将 DCRNN 与以下变体进行了比较：

1）DCRNN-NoConv，它通过用单位矩阵替换扩散卷积（等式 2）中的转换矩阵来忽略空间依赖。这实质上意味着传感器的预测只能从其自身的历史读数中推断出来；
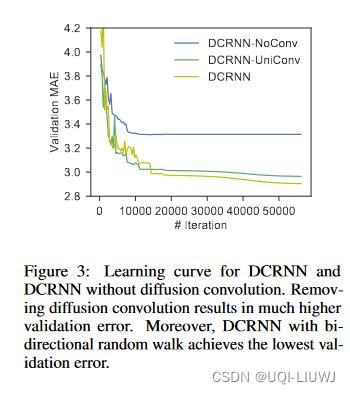
2）DCRNN-UniConv，仅使用前向随机游走转移矩阵进行扩散卷积；

图 3 显示了这三个模型在参数数量大致相同的情况下的学习曲线。如果没有扩散卷积，DCRNN-NoConv 的验证误差要高得多。此外，DCRNN 实现了最低的验证误差，这表明了使用双向随机游走的有效性。直觉是双向随机游走使模型能够灵活地捕捉来自上游和下游流量的影响。

• 为了研究图构造的效果，我们通过设置 来构造一个无向图
• 其中是新的对称权重矩阵。
• 然后我们开发了一个 DCRNN 的变体表示 GCRNN，它使用 ChebNet 图卷积（方程 5）进行序列到序列学习，参数量大致相同。
• 表 2 显示了 METR-LA 数据集中 DCRNN 和 GCRNN 之间的比较。
• DCRNN 始终优于 GCRNN。直觉是有向图更好地捕捉交通传感器之间的不对称相关性

 

• 图 4 显示了不同参数的影响。 K 大致对应于过滤器接收域的大小，而单元数对应于过滤器的数量。
• 较大的 K 使模型能够以增加学习复杂性为代价捕获更广泛的空间依赖性。我们观察到随着 K 的增加，验证数据集上的误差首先快速减小，然后略有增加。
• 对于不同的单位数量，观察到类似的行为。
•  

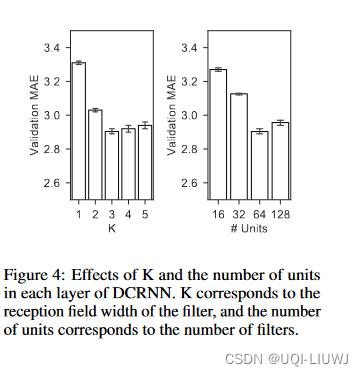
 （个人感觉是过拟合？）
 

3.5 模型解释

为了更好地理解模型，我们将预测结果和学习过滤器可视化。图 6 显示了提前 1 小时预测的可视化。我们有以下观察结果：

1）当交通速度中存在小幅振荡时，DCRNN 生成平均值的平滑预测（图 6（a））。这反映了模型的稳健性。
2）DCRNN 比基线方法（例如 FC-LSTM）更可能准确预测交通速度的突然变化。如图 6(b) 所示，DCRNN 预测高峰时段的开始和结束。这是因为 DCRNN 捕获了空间依赖性，并且能够利用邻域传感器的速度变化进行更准确的预测。

图 7 可视化了以不同节点为中心的学习过滤器的示例。星号表示中心，颜色表示权重。我们可以观察到

1）权重很好地定位在中心周围，
2）权重基于道路网络距离扩散。