常用深度学习模型调优方法

Posted 2022-11-24 archimekai

• 常用调优建议
  • 数据优化
    • 确保各个分类中的样本数目相近
    • 获取更多数据
    • 归一化数据
    • 对数据做变换以使数据服从均匀分布
  • 算法优化
    • 参考领域中的已有工作
    • 优化模型中每一层的大小
    • 模型层数的选择和优化
    • 权重初始值的选择和优化
    • 激活函数的选择和优化
    • 优化器的选择和优化
    • 早停法
  • 超参优化
    • 学习率的选择和优化
    • batch size的选择和优化
    • 学习率和batch size的联合优化
    • 动量值的选择和优化
    • 权重衰减参数的选择和优化
  • 精度调优相关参考文献

数据优化

确保各个分类中的样本数目相近

当数据集中各分类的样本数目不均衡时，需要进行调整以使每个分类对训练有程度相近的影响。可以考虑以下方法：

基于数据重采样的方法：

1. 对样本数较少的类过采样
2. 对样本数目较多的类欠采样
3. 混用上面两种方案。

通过上述重采样，使得训练过程中每个类出现的样本数相对均衡。需要注意的是，过采样有过拟合的风险(Cao et al., 2019)。

基于代价的方法：

1. loss函数不变，根据每个类中的样本数目重新设置loss权重，其中，权重为每一类别样本数的平方根的倒数。
2. 在loss函数中直接反映类不均衡的情况，迫使样本数较小的类同决策边界间的范围扩大。

获取更多数据

让模型效果更好的最直接方法就是获取更多数据，训练集越大，模型效果一般越好。

归一化数据

归一化数据是指将数据映射到同一尺度，常见的操作方法包括Resize、Rescale、Normalize等。按照激活函数的值域上下界来归一化数据通常可以取得不错的效果。例如，当使用sigmoid激活函数时，建议将输入归一化到0到1之间；当使用tanh激活函数时，推荐将输入数据归一化到-1到1之间。

此外，可以系统性地尝试不同的数据归一化方法，包括把数据归一化到0-1、归一化到-1到1之间，或者是将数据标准化到均值为0，方差为1的分布上。然后针对每种数据归一化方法评估模型的表现。

对数据做变换以使数据服从均匀分布

对于数值类型的数据，可以考虑对数据进行转换以调整数据的分布。例如某列数据是指数分布，可以通过一个log变换将该列数据变换为均匀分布。

算法优化

参考领域中的已有工作

如果所要实现的算法已经有很多相关的研究工作，不妨参考一下相关的论文，并把论文中使用的各种方法记录下来，根据经验尝试各种可能的组合。例如，你可能在训练GAN网络时发现精度差几个百分点难以达标，此时你可以多参考一些研究工作，尝试它们使用的技巧，例如更改loss函数（例如WGAN，WGAN-GP等），修改训练方法（例如将每个step内Generator和Discriminator各训练1次改为各训练3次）等。

优化模型中每一层的大小

在设计模型时，可以在一开始将每一层的尺寸（例如卷积层的输入输出大小）设计为相同的。有研究证明，将所有层的尺寸设置为相同的，其模型表现一般不会差于正金字塔（层的尺寸逐层增大）或者倒金字塔（层的尺寸逐层减小）的模型结构。

推荐将第一个隐层的大小大于输入尺寸。相较于第一个隐层的大小小于输入大小的情况，第一个隐层的大小大于输入大小时模型的表现更好。

模型层数的选择和优化

层数更多的模型有更大的机会来对数据中的抽象特征进行表达和重组，提供更强的表征能力，但是也更容易过拟合。层数较少的模型则容易出现欠拟合。

权重初始值的选择和优化

权重初始值对训练效果的影响较大，在MindSpore的模型交付实践中， 常常有因为权重初始值引起的精度差异。在有标杆脚本时，应该确保MindSpore脚本的权重初始化方式和标杆脚本的权重初始化方式一致。特别要小心未指定权重初始化方式的场景，此时使用的是各个框架的默认初始化方式，而MindSpore、PyTorch、TensorFlow等框架的默认权重初始化方式常常不同。

常见的权重初始化方式包括：（1）随机初始化（2）Xavier初始化(Glorot & Bengio, 2010)（3）Kaiming初始化(He et al., 2015)等。其中，Xavier初始化适用于使用tanh作为激活函数的网络而不适用于使用ReLU作为激活函数的网络，Kaiming初始化适合于使用ReLU作为激活函数的网络。不推荐使用常数初始化、全零初始化（bias除外），因为权重初始化为统一的常数（例如0/1）时，所有神经元学到的特征相同（梯度相同），进而导致模型表现较差。不推荐使用过大或过小的权重初始值。当权重初始值过小时，模型的收敛可能会很慢，在比较深的网络可能完全不能收敛。这是由于过小的权重容易导致激活值太小，梯度消失。当权重初始值过大时，模型可能完全无法收敛，这是由于较大的权重容易导致梯度爆炸，扰乱参数更新的方向。

在Batch Normalization提出前，权重初始值的均值和方差是需要着重考虑的因素。简单来说，模型输出的大小和权重的乘积（以及激活函数的输出范围）相关，当权重值过小时，模型输出的大小也会变得很小，当权重值过大时，模型输出的大小也会变得很大，Xavier和Kaiming初始化都是基于稳定权重方差和激活函数输出范围的目的推到得到的。当网络中使用Batch Normalization时，一定程度上能减缓对权重初始值的依赖，但仍然建议使用前述推荐的权重初始化方式。

如果不确定使用哪种权重初始化方式，可以固定其它因素，对多种权重初始化方式进行对比。

激活函数的选择和优化

ReLU激活函数通常是一个不错的选择。如果ReLU效果不是很好，可以尝试Leaky ReLU或Maxout等变种。对于RNN类网络，tanh函数也是一个不错的选择。除非您是这方面的专家，有明确的动机或者理论分析的支撑，通常不建议自行尝试学术界尚未证明效果的激活函数。 在深度不是特别深的CNN中，激活函数的影响一般不会太大。

优化器的选择和优化

优化器对模型精度和收敛速度（收敛所需的参数更新次数）都会有影响。通常Adam优化器是一个不错的选择。带有动量的优化器有助于提升大batch size下的训练速度。

在选择优化器时，一方面要注意优化器之间有功能上的包含关系(Choi et al., 2019)。例如RMSProp优化器功能包含了Momentum优化器的功能。这是因为，令RMSProp中的decay参数取1，epsilon参数取0，则RMSProp即等效于动量为momentum/learning_rate的Momentum优化器。Adam优化器同样也包含了Momentum优化器的功能。MindSpore的Momentum优化器和SGD优化器的功能是类似的。另一方面也要注意，功能更强大的优化器，一般有更多参数，要花费更长时间才能找到合适的超参。

早停法

一旦验证集上的表现下降时，就应该停止训练以免过拟合，也即早停法。

超参优化

狭义上讲，超参是指在训练开始前即手工确定好的变量。广义上讲，上文讨论过的模型设计选择也可以认为是超参，例如网络层数设计，激活函数选择等。需要说明的是，训练得到的结果不能算作超参，例如训练后得到的权重数据就不是超参。本节主要讲狭义超参的优化，下文中如没有特殊说明，指的都是狭义超参。

进行超参优化时要注意：没有通用的最佳超参。选择最优超参没有一劳永逸的方法，既需要经验，也需要不断试错。

学习率的选择和优化

学习率是控制如何使用损失函数的梯度调整网络权重的超参数。学习率的取值对模型能否收敛，模型收敛的速度有重要影响。相较于固定学习率，在训练过程中循环变化学习率总体来说是有益于模型收敛的。循环变化学习率的最大值和最小值可以这样确定(Smith, 2017)：选定一个足够大的学习率范围（例如从0到5），设置训练运行几个epoch（例如10个），在训练运行过程中，逐迭代地线性（或指数）增大学习率，就可以得到一个准确率和学习率的关系曲线，如下图。关注曲线中准确率开始上升和不再上升的的部分所对应的学习率，可以将准确率开始上升时的学习率当做学习率的下限，将准确率不再上升时的学习率当做学习率的上限，在上下限之间的学习率都可以认为是合理的。此外，在Neural Networks: Tricks of the Trade这本书中提供了一个经验法则：最优学习率一般为可以使网络收敛的最大学习率的二分之一。另一个经验法则是，0.01的学习率通常适用于大多数网络 。当然这些经验法则是否正确就需要各位读者自行判断了。

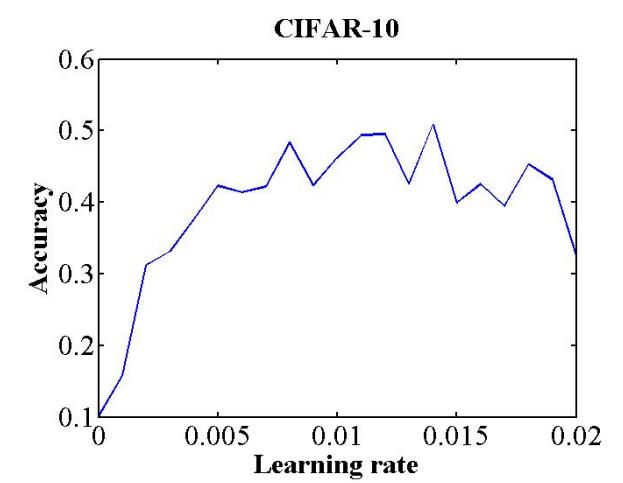
图14 学习率与准确率的关系。此曲线通过8个epoch的训练得到。图片引用自(Smith, 2017)。

以上文所述的合理学习率为起点，每个网络的最优值都需要根据具体情况（网络类型、batch size、优化器、其他相关超参等）实验和调整。

batch size的选择和优化

batch size是指一次训练，也即一次前向传播、反向传播、权重更新过程所使用的样本数目。batch size越大，就越有潜力达到快的训练速度，但是batch size不能无限增大。一方面，batch size越大，所需要的硬件内存就越多，硬件内存为可能的最大batch size设置了上界。另一方面，当batch size过大时，模型的泛化能力将下降(Keskar et al., 2016)。batch size较小时，可以起到正则化的效果，有助于减少过拟合(Masters & Luschi, 2018)，但是不能充分发挥硬件的运算能力。

基于上面的描述，需要较快的训练速度和正则化效果之间进行权衡。一般来讲，32是一个比较好的默认值(Bengio, 2012)，64、128、256 也都值得尝试。batch size 学习率之间存在相互影响，将在下一节阐述。

学习率和batch size的联合优化

一旦在某个batch size下找到最优的学习率后，后续调整batch size时，应该同步调整学习率，使得batch size和学习率的比值保持固定，这被成为linear scaling rule。基于郎之万动力学，学习率和batch size在满足linear scaling rule时可以得到相等的动力学演化时间(Xie et al., 2020)。在做出一些假设后，当学习率同batch size的比值固定时，只需要训练相同的epoch数，训练效果应该是一样的。并行场景下利用这一点同步增大batch size和学习率能够有效缩短训练时间。但是需要注意的是，batch size及学习率过大时，会破坏一些假设，例如中心极限定理成立要求batch size远小于训练数据集大小，连续时间近似成立要求学习率足够小等。当这些假设被破坏时，linear scaling rule也就不成立了，此时需要适当降低batch size或学习率。

动量值的选择和优化

当使用带有动量的优化器（例如Momentum）时，动量和学习率一般应朝相反的方向调整，不同动量下的最佳学习率不同。当使用循环学习率时，同样推荐按照相反的方向循环变化动量值 ，也即，当学习率从大到小变化时，动量应从小到大变化。当学习率固定时，动量值也应保持固定。

权重衰减参数的选择和优化

权重衰减（weight decay）是指在在模型训练过程中对目标代价函数增加一个L2参数范数惩罚，权重衰减参数控制这一惩罚项的系数，请参考SGD优化器的weight_decay参数。实验证明，权重衰减参数最好在训练过程中保持恒定。0.001/0.0001/0.00001都是常见的取值。当数据集较小、模型深度较浅时，推荐使用大一些的参数值，当数据集较大、模型深度较深时，推荐使用小一些的参数值。这可能是因为，较大的数据集本身便提供了某种程度的正则化，从而降低了需要权重衰减提供的正则化。

精度调优相关参考文献

Bengio, Y. (2012). Practical Recommendations for Gradient-Based Training of Deep Architectures.

Cao, K., Wei, C., Gaidon, A., Arechiga, N., & Ma, T. (2019). Learning Imbalanced Datasets with Label-Distribution-Aware Margin Loss. Advances in Neural Information Processing Systems, 32. https://arxiv.org/abs/1906.07413v2

Choi, D., Shallue, C. J., Nado, Z., Lee, J., Maddison, C. J., & Dahl, G. E. (2019). On Empirical Comparisons of Optimizers for Deep Learning. https://www.tensorflow.org/

Glorot, X., & Bengio, Y. (2010). Understanding the difficulty of training deep feedforward neural networks. Journal of Machine Learning Research, 9, 249–256.

He, K., Zhang, X., Ren, S., & Sun, J. (2015). Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. Proceedings of the IEEE International Conference on Computer Vision, 2015 Inter, 1026–1034. IEEE Xplore Temporarily Unavailable

Keskar, N. S., Mudigere, D., Nocedal, J., Smelyanskiy, M., & Tang, P. T. P. (2016). On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima. 5th International Conference on Learning Representations, ICLR 2017 - Conference Track Proceedings, 1–16. http://arxiv.org/abs/1609.04836

Masters, D., & Luschi, C. (2018). Revisiting small batch training for deep neural networks. ArXiv, 1–18.

Montavon, G., Orr, G. B., & Müller, K.-R. (Eds.). (2012). Neural Networks: Tricks of the Trade. 7700. Neural Networks: Tricks of the Trade | SpringerLink

Nwankpa, C., Ijomah, W., Gachagan, A., & Marshall, S. (2018). Activation Functions: Comparison of trends in Practice and Research for Deep Learning. http://arxiv.org/abs/1811.03378

Smith, L. N. (2017). Cyclical learning rates for training neural networks. Proceedings - 2017 IEEE Winter Conference on Applications of Computer Vision, WACV 2017, 464–472. IEEE Xplore Temporarily Unavailable

Xie, Z., Sato, I., & Sugiyama, M. (2020). A Diffusion Theory For Deep Learning Dynamics: Stochastic Gradient Descent Exponentially Favors Flat Minima. https://arxiv.org/abs/2002.03495v14