LCA的两种求法

Posted 2020-11-19 q1143316492

HDU 2586 

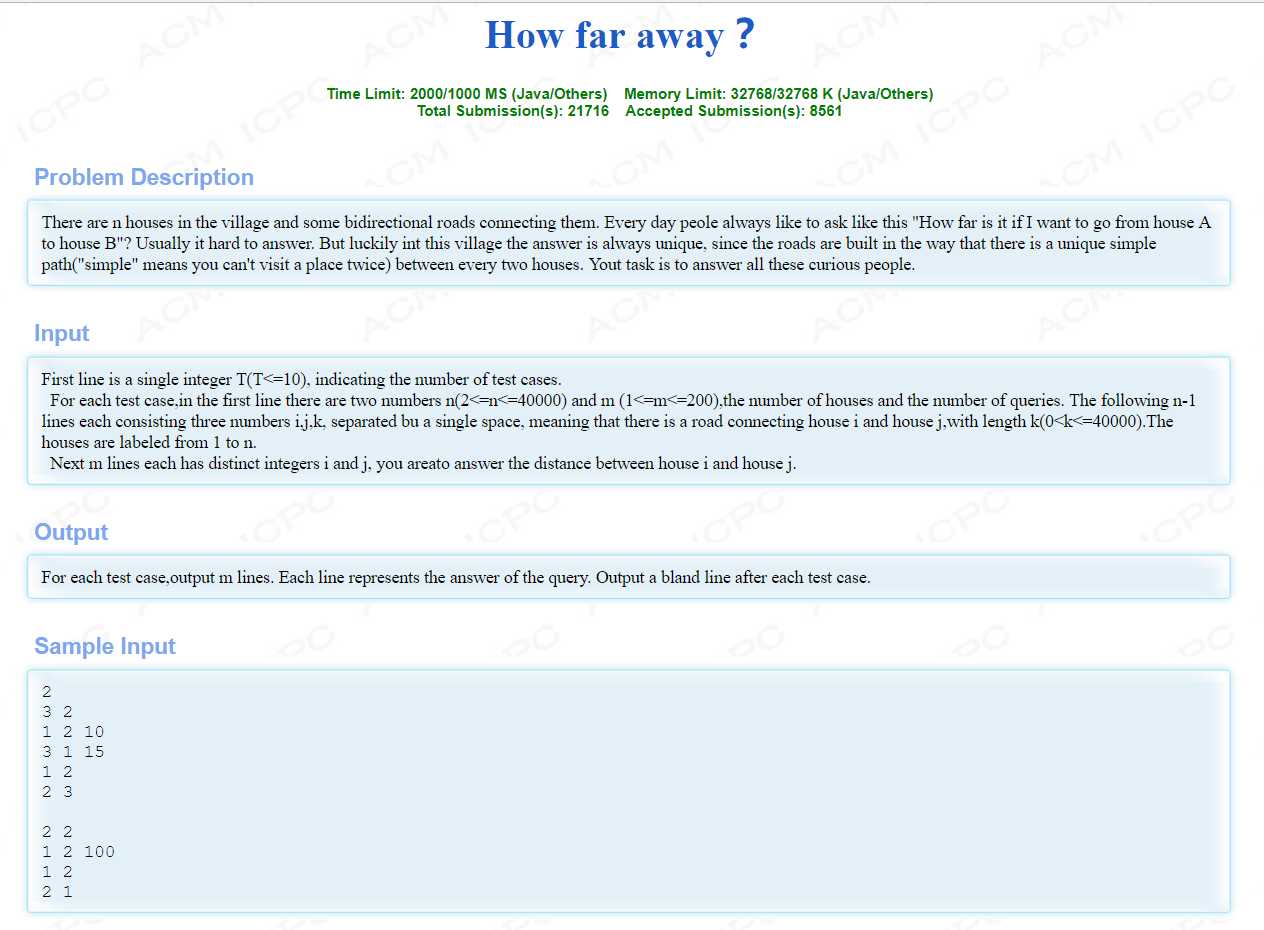
题意：一棵树，多次询问任意两点的路径长度。

LCA：最近公共祖先Least Common Ancestors。两个节点向根爬，第一个碰在一起的结点。

求出x, y的最近公共祖先lca后，假设dist[x]为x到根的距离，那么x->y的距离为dist[x]+dist[y]-2*dist[lca]

 

求最近公共祖先解法常见的有两种

1, tarjan+并查集

2,树上倍增

 

首先是树上倍增。

 

 1 #include <cstdio>
 2 #include <cstring>
 3 #include <iostream>
 4 #include <algorithm>
 5 
 6 using namespace std;
 7 const int maxn = 4e4 + 7;
 8 
 9 int T, n, m, u, v, w;
10 
11 int first[maxn], sign, st[maxn][21], level[maxn], dist[maxn];
12 
13 struct Node {
14     int to, w, next;
15 } edge[maxn * 2];
16 
17 inline void init() {
18     for(int i = 0; i <= n; i ++ ) {
19         first[i] = -1;
20     }
21     sign = 0;
22 }
23 
24 inline void add_edge(int u, int v, int w) {
25     edge[sign].to = v;
26     edge[sign].w = w;
27     edge[sign].next = first[u];
28     first[u] = sign ++;
29 }
30 
31 void dfs(int now, int father) {
32     level[now] = level[father] + 1;
33     st[now][0] = father;
34     for(int i = 1; (1 << i) <= level[now]; i ++ ) {
35         st[now][i] = st[ st[now][i - 1] ][i - 1];
36     }
37     for(int i = first[now]; ~i; i = edge[i].next) {
38         int to = edge[i].to, w = edge[i].w;
39         if(to == father) {
40             continue;
41         }
42         dist[to] = dist[now] + w;
43         dfs(to, now);
44     }
45 }
46 
47 int LCA(int x, int y) {
48     if(level[x] > level[y]) {
49         swap(x, y);
50     }
51     for(int i = 20; i >= 0; i -- ) {
52         if(level[x] + (1 << i) <= level[y]) {
53             y = st[y][i];
54         }
55     }
56     if(x == y) {
57         return x;
58     }
59     for(int i = 20; i >= 0; i -- ) {
60         if(st[x][i] == st[y][i]) {
61             continue;
62         } else {
63             x = st[x][i], y = st[y][i];
64         }
65     }
66     return st[x][0];
67 }
68 
69 int main() {
70     scanf("%d", &T);
71     while(T--) {
72         scanf("%d %d", &n, &m);
73         init();
74         for(int i = 1; i <= n - 1; i ++ ) {
75             scanf("%d %d %d", &u, &v, &w);
76             add_edge(u, v, w);
77             add_edge(v, u, w);
78         }
79         memset(level, 0, sizeof(level));
80         memset(st, 0, sizeof(st));
81         dist[1] = 0;
82         dfs(1, 0);
83         for(int i = 1; i <= m; i ++ ) {
84             int u, v;
85             scanf("%d %d", &u, &v);
86             int lca = LCA(u, v);
87             printf("%d
", dist[u] + dist[v] - 2 * dist[lca]);
88         }
89     }
90 
91     return 0;
92 }

View Code

 

 

然后是tarjan的解法(参考算法竞赛进阶指南)

个人理解，tarjan算法就是对搜索的过程中维护了一些性质。在搜索的过程中把点分为三类

1,已经范围且回溯的点，代码中vis[x]=2

2,已经访问还没有回溯的点,代码中vis[x]=1

3,未被标记的点

每一个回溯的点都用并查集连到他的父节点，这样如果我们x点正在访问，我们需要知道x,y的lca,而y已经被访问了，那么并查集y的根就是x,y的lca

 

  1 #include <cstdio>
  2 #include <cstring>
  3 #include <iostream>
  4 #include <algorithm>
  5 
  6 using namespace std;
  7 const int MAXN = 5e4 + 7;
  8 const int INF = 0x3f3f3f3f;
  9 
 10 int n, m, first[MAXN], sign;
 11 
 12 int pre[MAXN], ans[MAXN], vis[MAXN], dist[MAXN], lca[MAXN], indexs;
 13 
 14 vector<pair<int, int> >query[MAXN]; ///y, id
 15 
 16 struct Node {
 17     int to, w, next;
 18 } edge[MAXN * 2];
 19 
 20 inline void init() {
 21     for(int i = 0; i <= n; i++ ) {
 22         first[i] = -1;
 23         pre[i] = i;
 24         query[i].clear();
 25         ans[i] = INF;
 26         vis[i] = 0;
 27     }
 28     sign = 0;
 29 }
 30 
 31 inline void add_edge(int u, int v, int w) {
 32     edge[sign].to = v;
 33     edge[sign].w = w;
 34     edge[sign].next = first[u];
 35     first[u] = sign++;
 36 }
 37 
 38 int findx(int x) {
 39     return pre[x] == x ? x : pre[x] = findx(pre[x]);
 40 }
 41 
 42 inline void join(int x, int y) {
 43     int fx = findx(x), fy = findx(y);
 44     pre[fx] = fy;
 45 }
 46 
 47 inline bool same(int x, int y) {
 48     return findx(x) == findx(y);
 49 }
 50 
 51 void tarjan(int now) {
 52     vis[now] = 1;
 53     for(int i = first[now]; ~i; i = edge[i].next) {
 54         int to = edge[i].to;
 55         if(!vis[to]) {
 56             dist[to] = dist[now] + edge[i].w;
 57             tarjan(to);
 58             pre[to] = now;
 59         }
 60     }
 61     for(int i = 0; i < query[now].size(); i++ ) {
 62         int y = query[now][i].first, id = query[now][i].second;
 63         if(vis[y] == 2) {
 64             int lca = findx(y);
 65             ans[id] = min(ans[id], dist[now] + dist[y] - 2 * dist[lca]);
 66         }
 67     }
 68     vis[now] = 2;
 69 }
 70 
 71 int main()
 72 {
 73     int T;
 74     scanf("%d", &T);
 75     while(T--) {
 76         scanf("%d %d", &n, &m);
 77         init();
 78         for(int i = 1; i <= n - 1; i++ ) {
 79             int u, v, w;
 80             scanf("%d %d %d", &u, &v, &w);
 81             add_edge(u, v, w);
 82             add_edge(v, u, w);
 83         }
 84         for(int i = 1; i <= m; i++ ) {
 85             int x, y;
 86             scanf("%d %d", &x, &y);
 87             if(x == y) {
 88                 ans[i] = 0;
 89                 continue;
 90             }
 91             query[x].push_back(make_pair(y, i));
 92             query[y].push_back(make_pair(x, i));
 93             ans[i] = INF;
 94         }
 95         tarjan(1);
 96         for(int i = 1; i <= m; i++ ) {
 97             printf("%d
", ans[i]);
 98         }
 99     }
100     return 0;
101 }

View Code